

Вопрос 1
Классификация автоматических систем. Примеры по классификации
Классификация автоматических систем
1. По качеству регулирования
а) системы с регулированием по возмущению (без обратной связи)
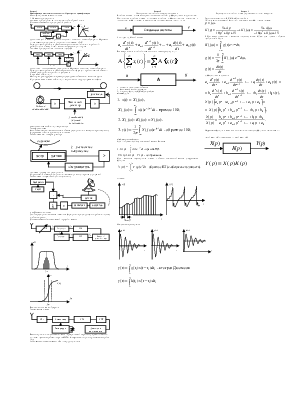
Система автоматического регулирования усиления:

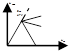
Достоинства этой системы в простоте и отсутствии склонности к самовозбуждению. Недостаток: низкое качество регулирования по сравнению с системами с ОС.
Регулирующее воздействие вырабатывается на основе анализа внешних воздействий, действующих на систему. Анализ состояния объекта не производится.
б) система с регулированием по отклонению (с ОС)

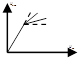
Достоинство – высокое качество регулирования. Недостаток: склонность к самовозбуждению.
Регулирующее воздействие вырабатывается на основе информации о действительном состоянии объекта регулирования в сравнении с требуемым.
2. а) системы стабилизации
Необходимы для поддержания параметров регулируемого объекта на постоянном уровне.
Упрощенная схема системы стабилизации скорости ленты в аудио (видео) магнитофоне:
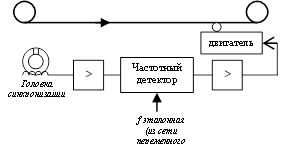
(замкнутая система стабилизации через ленту).
б) следящая система
Это система, которая изменяет состояние объекта регулирования по какому-то заданному закону (определяется внешним управляющим сигналом).
Такая система есть в каждом дисководе.
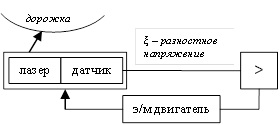
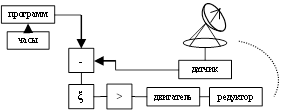
в) система программного регулирования
Когда состояние объекта регулирования изменяется про закону, заданному программой.
Такая система поворачивает спутниковую антенну.
3. а) Статические системы
Ошибка регулирования является источником формирования регулирующего воздействия, поэтому ошибка всегда есть.
Система статической автоматической подстройки частоты:

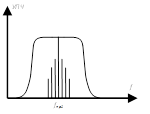
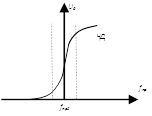
Велика опасность самовозбуждения.
б) астатическая система
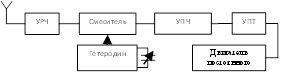
Вместо варикапа используется механически перестраиваемый конденсатор переменной ёмкости.
Двигатель перестанет работать, когда на УПТ U=0, следовательно, происходит точная настройка на fпр1.
Астатическая система включает в себя интегрирующие звенья.
Вопрос 2
Методы анализа линейных систем радиоавтоматики
Линейная система – система, которая описывается линейными дифференциальными уравнениями. Стационарная линейная система описывается линейным дифференциальным уравнением с постоянными коэффициентами (не меняющиеся во времени частоты, уровни и т.д.).
![]()
Y копирует x. ДУ такой системы:
![]() .
.
Все методы анализа линейной системы основаны на методе суперпозиции:
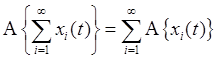 .
.

x – состояние регулируемого объекта,
y – фактическое состояние (датчик),
A – оператор, функция (K(jω), K(p), g(t), h(t)).
Метод Фурье:
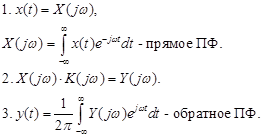
Изображение по Лапласу:
X(p) – изображение (спектр комплексной частоты Лапласа).
![]()
K(p) – частотная характеристика системы в области комплексной частоты (передаточная функция).
![]()
Дюамель:
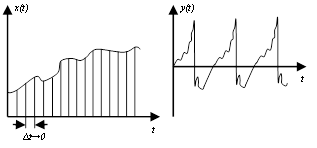
Импульсная характеристика:
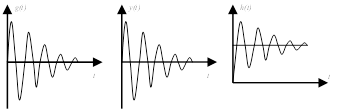
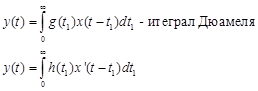
Вопрос 3
Характеристики линейных систем радиоавтоматики, связь между ними
Основные характеристики ЛС: K(jω), K(p), g(t1), h(t1).
1. Связь между передаточной функцией и комплексным коэффициентом передачи:
![]()
2. Связь между временными и частотными характеристиками K(jω) и g(t) – прямое и обратное преобразование Фурье:
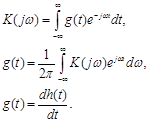
Дифференциальное уравнение:
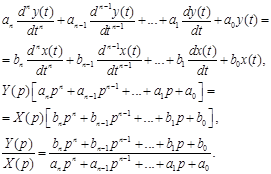
Передаточная функция системы есть отношение полиномов (коэффициенты в числителе - из правой части ДУ, в знаменателе – из левой части ДУ).

![]()
Вопрос 4
Структурные схемы, отличие от функциональных. Примеры
Структурные схемы – набор прямоугольников, соединённых стрелками, показывающих направление распространения информации. В прямоугольниках указываются соответствующие передаточные функции.
Структурные звенья 1го порядка:
![]() .
.
1. Безынерционное (пропорциональное) звено
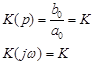

2. Инерционное
![]()
K – коэффициент усиления на постоянном токе, T – постоянная времени инерционного звена.
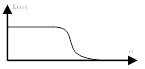
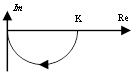
3. Идеальное интегрирующее
![]()
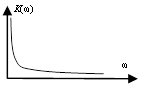

4. Дифференцирующее
а) идеальное дифференцирующее звено
![]()
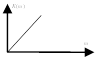

5. Реальное дифференцирующее звено
![]()
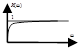
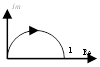
5. Упругие звенья
![]()
а) T1 > T2 – упругое дифференцирующее
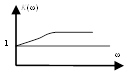
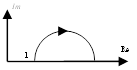
б) T1 < T2 – упругое интегрирующее
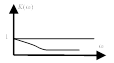

6. Форсирующее
![]()
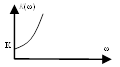
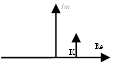
7. Колебательное
![]()
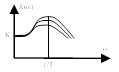
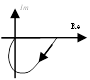
В
структурных схемах используется операторный метод. В качестве описания
используется передаточная функция каждого элемента. Функциональные схемы
позволяют рассмотреть схему на уровне принципа работы и связей между основными
элементами.
Вопрос 5
Инерционные и интегрирующие звенья, их характеристики
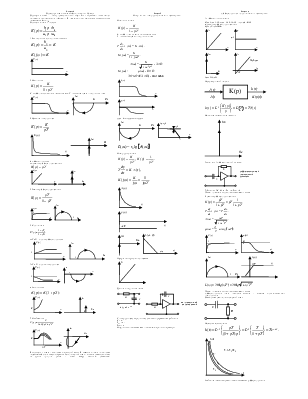
Инерционные звенья
![]() .
.
K – коэффициент усиления на постоянном токе.
T – постоянная времени инерционного звена.
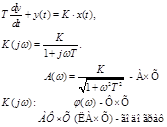
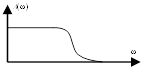

φ(ω) = 0 - arctg(ωt) = - arctg(ωt).
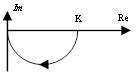
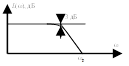
![]() .
.
Интегрирующие звенья:
![]()
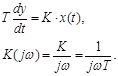
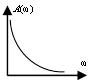

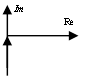
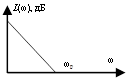
Подадим на вход ступеньку, получаем
![]()
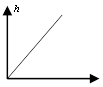
Сравним с инерционным звеном.
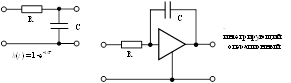
К интегрирующему операционному усилителю предъявляются требования:
K→ ∞,
Rвх → ∞,
Rвых→ ∞.
Инерционность появляется сама из-за наличия паразитных параметров.
Вопрос 6
Дифференцирующие и упругие звенья, их характеристики
1. Дифференцирующие звенья
K(jω): A(ω) – АЧХ, φ(ω) – ФЧХ, АФЧХ – годограф, ЛАЧХ.
а) идеальное дифференцирующее звено
K(p) = pT, y(t)=Tdx/dt.
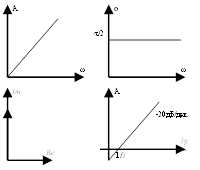
L(ω) = 20lg(ωT).
Подадим единичный импульс.
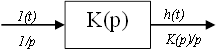
![]() .
.
Импульсная характеристика имеет вид:
Операционный дифференциальный усилитель:
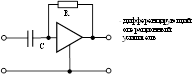
Требования к ОУ: K = -∞, Rвх → ∞, Rвых → 0
Область применения: коррекция автоматических систем.
б) реальное дифференцирующее звено
![]() .
.
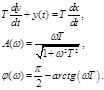
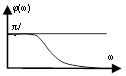
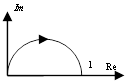
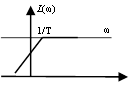
![]() .
.
Область применения: коррекция автоматических систем.
Дифференцирующие звенья поглощают астатизм и являются «противоположными» интегрирующим.
Самая простая реализация вынужденной схемы:
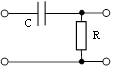
Переходная характеристика:
![]()
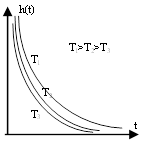
Чем больше постоянная времени, тем выше качество дифференцирования.
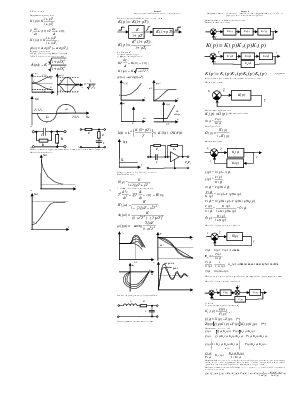
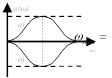
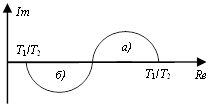
2. Упругие звенья
Передаточная характеристика:
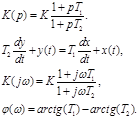
Возможны два варианта:
а) T1 > T2 (звено упругое дифференцирующее);
б) T2 > T1 (звено упругое интегрирующее).
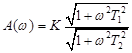
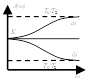
а)
а)
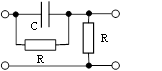 б)
б) 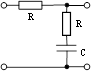
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.