Пример:
Если m=2, то годограф для устойчивого состояния должен 1 раз охватить точку (-1,0).

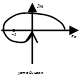
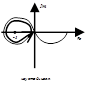
m=3:
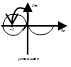
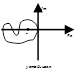
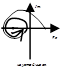
Вопрос 15
Частотный критерий Михайлова. Примеры
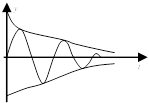
Траектория описывается уравнением
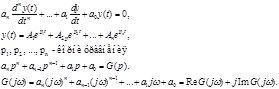
Все корни должны быть в левой полплоскости:
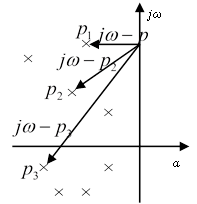
![]()
Фазовый набег вектора G(jω):
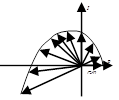
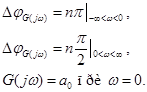
- Годограф характеристической частотной функции замкнутой системы (годограф Михайлова)
Частотный критерий Михайлова:
Замкнутая система будет устойчива, если годограф характеристической частотной функции замкнутой системы при изменении частоты от 0 до ∞, начинаясь с вещественной оси, последовательно, против часовой стрелки, обходит n квадрантов и в последнем квадранте уходит в бесконечность.
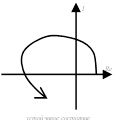
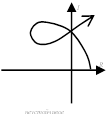
Следствием из применения критерия устойчивости Михайлова является правило чередующихся корней: при движении точки по годографу в направлении возрастания частоты годограф должен последовательно пересекать вещественную и мнимую оси, ни разу не пересекая дважды одну и ту же ось.
Пример:
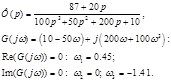
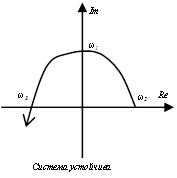
Вопрос 18
Качество регулирования в установившемся и вынужденном режимах. Примеры
Под качеством регулирования подразумевают величину ошибки регулирования при воздействии на систему детерминированного сигнала.
Чем меньше ошибка, тем выше качество.
![]()
Ошибка ξ(p): ξ(p) = X(p) – Y(p).
Выделение ошибки – функция сумматора.
Определить ошибку можно несколькими способами:
1. а) записать ДУ замкнутой системы;
б) подставить в это уравнение ожидаемое решение в виде какой-то функции с неизвестными коэффициентами;
в) определить эти коэффициенты;
2. Классический операторный метод
а) найти изображение по Лапласу известной функции x(t);
б) по известной структуре системы K(p) находим передаточную функцию ошибки Kξx(p):
![]() ;
;
в) обратным преобразованием Лапласа определяем ξ(t) по таблицам.
3. Метод коэффициентов ошибки
а) раскладываем передаточную функцию Kξx(p) в ряд по степеням комплексной переменной p;
б) записываем ДУ в операторной форме:
![]() ,
,
где S0,…Sn – коэффициенты ошибки.
в) переходим от операторной к классической форме:
![]() ;
;
г) находим коэффициенты через известные коэффициенты полиномов G(p) и A(p).
Выводы:
1. Ошибка регулирования зависит от формы управляющего сигнала и от порядка астатизма системы;
2. Чем динамичнее входной сигнал, тем больший порядок астатизма требуется для приближения к нулевой ошибке;
3. Для нулевой ошибки необходим порядок астатизма на единицу больше числа ненулевых производных входного сигнала;
4. Если порядок астатизма равен числу ненулевых производных, ошибка постоянна;
5. Если порядок астатизма меньше, чем число ненулевых производных, ошибка регулирования будет возрастать со временем;
6. Чем больше коэффициент усиления, тем меньше ошибка.
Вопрос 19
Связь между структурой системы, входным воздействием и ошибкой регулирования. Примеры
Ошибка регулирования зависит от формы регулирующего воздействия и порядка астатизма системы. Порядок астатизма определяется количеством интегрирующих звеньев.
Рассмотрим метод коэффициентов ошибки.
Пример:
На входе приложено постоянное воздействие x(t) = A.
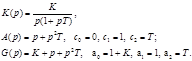
Так как в знаменателе нет свободного члена (из-за наличия интегрирующего звена), то c0 =0, значит коэффициент S0 = 0, остальные Si не равны 0.
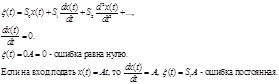
Отсюда мы можем сделать вывод, что для получения нулевой ошибки регулирования порядок астатизма должен быть на единицу больше числа ненулевых производных входного сигнала x(t); если же они равны, то ошибка будет постоянрной; если порядок астатизма больше числа ненулевых производных x(t), то ошибка будет расти.
Самыми мощными являются первые компоненты, поэтому есть смысл использовать астатические системы даже при очень динамических входных сигналах.
Вопрос 20
Качество переходных режимов, методы определения параметров качества
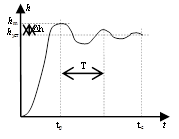
tр – время достижения максимального выброса, tc – время завершения переходного процесса, hm – максимальное значение переходной характеристики.
![]() .
.
![]() - частота колебания на вершине переходного
процесса.
- частота колебания на вершине переходного
процесса.
Переходные процессы важнее там, где система должна быть быстродействующей.
Способы определения качества переходных процессов
1. Аналитический способ
В его основе лежит передаточная функция системы и знание теории цепей:
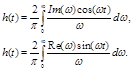
2. Графический способ
(по ЛАЧХ).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.