Новосибирский государственный технический университет
Кафедра Общей электроники
Отчёт по лабораторной работе № 17
по ОТЦ
"Компьютерный анализ переходных процессов"
Вариант 17.89
Факультет: РЭФ
Группа: РТ5-24
Студенты: Доценко С.А.
Преподаватель: Богданов В.В.
Новосибирск – 2004
Цель работы
Изучить методику составления уравнений переменных состояния цепи и их численного решения в среде MathCAD.
1. Провести предварительные теоретические выкладки.
2. Произвести необходимый объём работ в среде MathCAD.
1. Теоретическая часть
Схема замещения для момента времени t ≥ 0
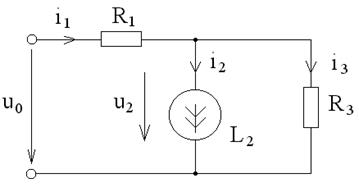
Составим уравнения по законам Кирхгофа для данной цепи
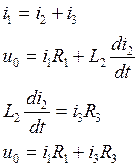
Преобразуем эти уравнения
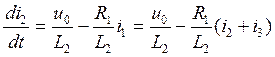
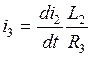
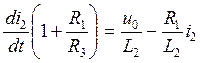
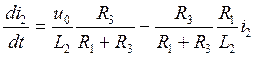
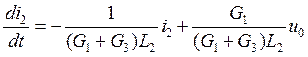
Получили уравнение состояния цепи, которое в более общем случае имеет вид:
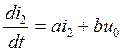 , где
, где 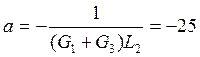 1/с ,
1/с , 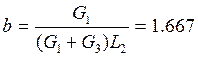 См/с
См/с
Интегрируя это уравнение на бесконечно коротком интервале в пределах от t = 0– до t = 0+,
находим стартовое значение тока катушки: ![]() .
.
В дальнейшем определим не только напряжение на катушке, но и ток через резистор R1, т.к. это делатся не сложно и попутно с основной задачей.
Напряжение u3(t)
резистора R3 (напряжение на катушке u2(t) равно напряжению на
резисторе u3(t)) и
ток ![]() резистора R1
являются линейными функциями тока катушки
резистора R1
являются линейными функциями тока катушки ![]() и задающего
напряжения u0(t):
и задающего
напряжения u0(t):
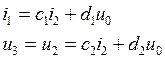
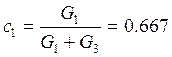
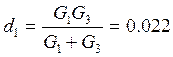 См
См
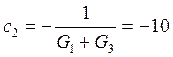 Ом
Ом 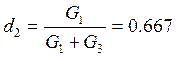
Найдём численное решение уравнения переменной состояния цепи методом Рунге-Кутта, реализованном в пакете MathCAD через функцию rkfixed.
2. Текст программы в среде MathCAD
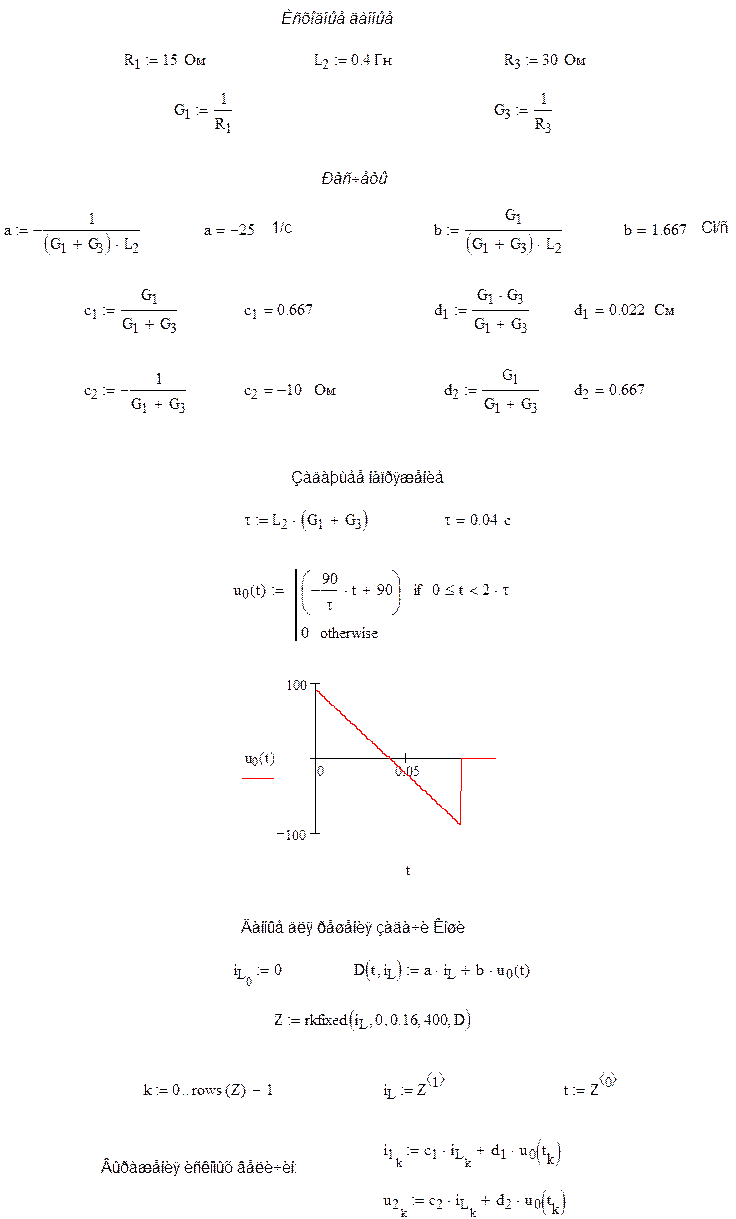
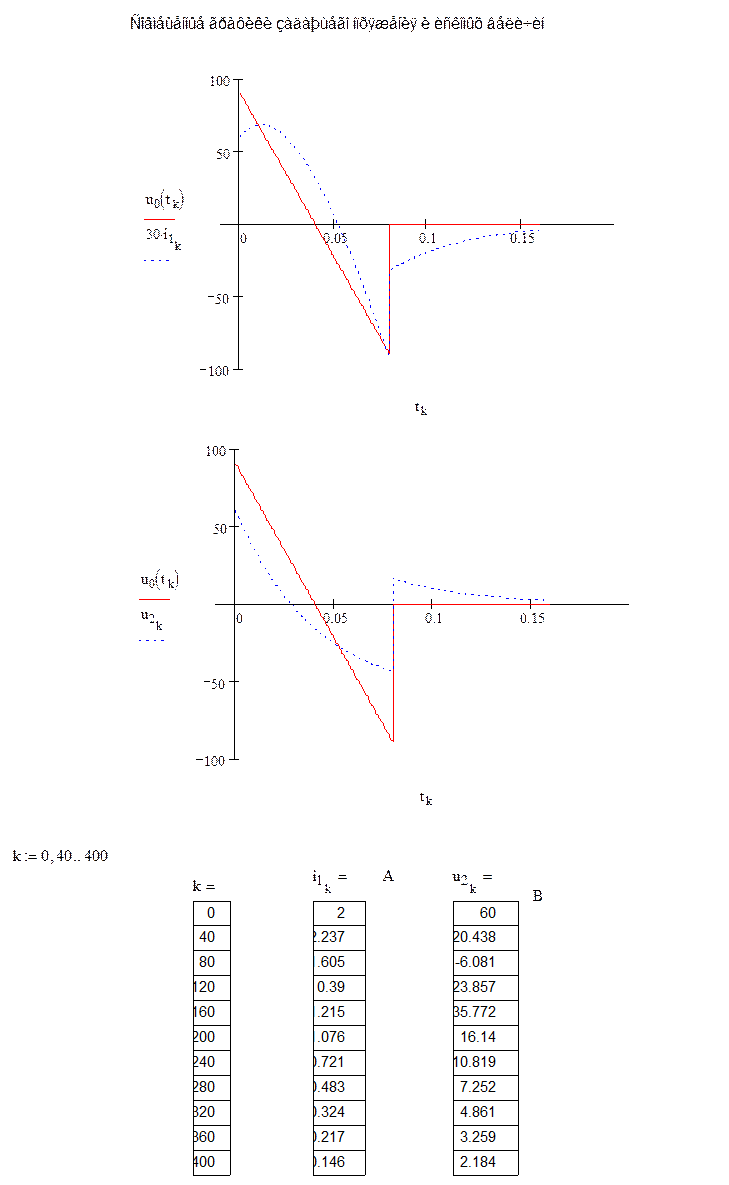
Заключение: математический пакет MathCAD позволяет относительно просто находить численные решения уравнений переменных состояния цепи посредством нескольких алгоритмов (методов), один из которых был использован в данной работе. Точность решения можно изменять в процессе вычислений. Полученный результат вполне соответствует идеальным характеристикам исходной цепи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.