Исследовать распределение амплитуд или действующих значений напряжений и токов в отрезке длинной линии c пренебрежимо малыми потерями (линии без потерь) в зависимости от характера и величины нагрузки. Изучить зависимость входного сопротивления (его вещественной и мнимой составляющих) от пространственной координаты при различных нагрузках.
Линия без потерь, моделируемая воображаемой схемой замещения, для которой известны параметры. В виртуальном эксперименте используется универсальная компьютерная система MathCad.
Рабочее задание
1. Вывести на экран монитора программу анализа режимов работы линии без потерь (MathCad, Lab_20.mcd). Скопировать файл, копию сохранить под другим именем (Save As).
2. Ввести исходные данные условной линии, в качестве которых принять данные своего варианта курсовой работы:
волновое сопротивление RС Ом;
частота f , Мгц;
относительная длина линии l0=l/l.
В дальнейшем анализе
будут приняты обозначения: c
–скорость электромагнитной волны в вакууме; ky –коэффициент укорочения волны (для простоты здесь
принято ky=1); l=c/f –длина волны, b=2p/l -коэффициент фазы (в радианах);![]() -коэффициент
отражения волны.
-коэффициент
отражения волны.
Поскольку в лабораторной работе не задается величина входного напряжения линии, в расчетных формулах произвольно принимается I2П=0.02 А –ток прямобегущей волны в сечении нагрузки; тогда напряжение прямобегущей волны
U2П=RсI2П.
3. Исследовать режим смешанных волн.
3.1 Поочередно устанавливая сопротивления нагрузки:
а)ZН=RН+XНj – комплексное сопротивление ( из задания на курсовую работу);
б, в)резистивные сопротивления ZН=2RС и ZН=0.5 RС,
получить на экране монитора графики распределения действующих значений напряжения U(x) и тока I(x) вдоль отрезка однородной линии без потерь при заданной нагрузке. Отсчет координаты “x” здесь и в дальнейшем ведется в метрах от конца линии к началу. Записать максимальное и минимальное значения напряжения, а также – координаты xmax и xmin ближайших к началу координат максимума и минимума напряжения.
3.2 По результатам исследования вычислить модуль и аргумент коэффициента отражения волны, а также комплексное сопротивление нагрузки. Сравнить результаты вычислений с исходными данными (вычисленные величины для отличия их от исходных данных снабдить каким- либо индексом или штрихом).
3.3 Построить графики распределения вещественной R(x) и мнимой X(x) составляющих сопротивления вдоль той же линии и при тех же сопротивлениях нагрузки.
3.4 Все материалы раздела скопировать на личную дискету.
4. Исследовать режимы стоячих волн.
Поочередно устанавливая сопротивления нагрузки ZН = ¥; ZН = 0; ZН = j XН; ZН = – j XН (XН –мнимая часть исходного ZН), повторить все наблюдения и возможные вычисления подобно предыдущему пункту, изменив, соответственно, заглавия подпунктов.
Результаты скопировать на личную дискету.
5. Исследовать режим бегущих волн (режим согласованной нагрузки).
Установить ZН=RC. Построить и проанализировать графики распределения напряжения, тока и сопротивления. Сделать заключение об особенностях этого режима
Результаты скопировать на личную дискету.
Для линий с пренебрежимо малыми потерями коэффициент ослабления можно принять практически равным нулю, тогда коэффициент распространения
g = j b
и основные уравнения линии преобразуются к виду:
![]()
![]()
![]()
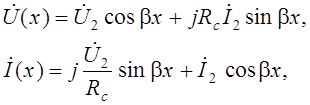
где x отсчитывается от конца линии (от нагрузки).
Для случаев холостого хода (I2 = 0) и короткого замыкания (U2 = 0) эти уравнения упрощаются и для модулей действующих значений имеют вид:
UХ(x) = U2 cos b x, UК (x) = Rc I2 sin b x
IХ(x) =![]() sin b x, IК (x) = I2 cos b x.
sin b x, IК (x) = I2 cos b x.![]()
Эти уравнения легко представить в виде графиков, где x может измеряться в метрах или в долях длины волны λ. Так же просто можно выразить входные сопротивления:
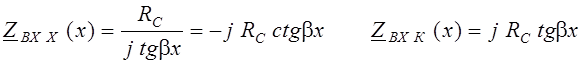
Легко видеть, что входные сопротивления в этих предельных режимах являются чисто реактивными, причем на протяжении первой четверти длины волны Zвх х носит емкостный, а Zвх к – индуктивный характер.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.