Компьютерный анализ режимов работы отрезка линии без потерь, страница 2

Для режимов произвольной нагрузки зависимости модулей напряжения и тока, а также вещественной и мнимой составляющих входного сопротивления удобно выразить через модуль коэффициента отражения волны ρ. Именно в таком виде эти зависимости и используются в настоящей лабораторной работе.

)

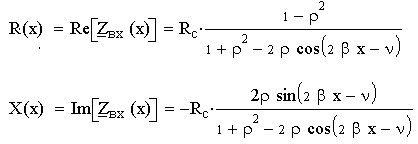
где U_2п и I_2п – модули прямых волн напряжения и тока в сечении нагрузки;

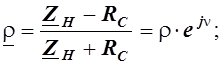
Количественная оценка степени  согласования нагрузки с линией осуществляется с помощью коэффициента бегущей волны:

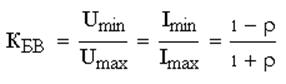
откуда можно выразить модуль ρ

Аргумент коэффициента отражения волны измеряется в радианах.

К_БВ = 1 соответствует бегущим волнам,

К_БВ = 0 соответствует стоячим волнам.

    Рассматривая кривые распределения модулей напряжения и тока,а также входных сопротивлений вдоль линии без потерь, Рис.20,1 (а,б), можно заметить:

а)	б)
Рис. 20.1

1)Максимумы и минимумы напряжений (токов) отстоят друг от друга на четверть длины волны (на  );

   2)При холостом ходе и резистивной нагрузке первые экстремальные значения модулей напряжения и тока приходятся на конец линии (х=0);

   3)При комплексном сопротивлении нагрузки экстремальные значения смещаются на некоторое расстояние x_max  или  x_{min ;}

   4)Мнимая часть входного сопротивления линии через каждые четверть длины волны обращается в нуль, что означает, что в линии существуют “резонансные сечения “ На эти же сечения приходятся и экстремумы кривых распределения модулей напряжения и тока.

   По экспериментальным данным можно зафиксировать экстремальные значения, например, модуля напряжения и расстояния между ними, а также расстояние до ближайшего к нагрузке максимума или минимума кривой. Это позволяет использовать линию без потерь (с пренебрежимо малыми потерями) в качестве измерительной линии для измерений сопротивлений в диапазоне ультракоротких волн

   В лабораторной работе ( в виртуальном эксперименте) по полученным графикам можно определить:

   -длину волны (следовательно, и частоту источника),

   -модуль коэффициента отражения волны:

 

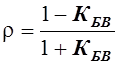
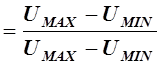
       аргумент коэффициента отражения волны:

           а) если первым от нагрузки следует максимум напряжения,то

n=2bx_{max ,}

              б) если первым от нагрузки следует минимум напряжения, то

n=2b(x_min-l/4)=2bx_min-p;

      комплексное сопротивление нагрузки:

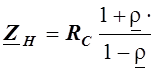,      где  

Программа домашней подготовки к выполнению работы

По  учебным  пособиям и конспекту лекций изучить тему: “Линия без потерь”.Приготовить дискету и  принести её на лабораторное занятие.Из методического пособия  по курсовой работе выписать данные своего варианта (эти же данные имеются на стенде по курсовому проетированию).

Контрольные вопросы

1. Дайте определение цепи с распределенными параметрами.

2. Каковы особенности линии без потерь?

3. При каких условиях в длинной линии возникают стоячие волны?

4. Передается ли энергия в линии без потерь, замкнутой на реактивное сопротивление?

5. Укажите особенности первичных и вторичных параметров линии без потерь в сравнении с таковыми для линии с потерями.

6. При каких условиях в линии существуют бегущие волны?

7. В чем заключаются смысл и способы согласования нагрузки с линией?

8. На каком расстоянии друг от друга в долях длины волны располагаются соседние максимумы напряжения или тока в режимах стоячих или смешанных волн?

9. Каково расстояние в долях длины волны между максимумом и минимумом напряжения (тока) в режиме стоячих или смешанных волн?

10. Какой характер имеют входные сопротивления при смешанных волнах в точках максимума или минимума напряжений (токов)?

11. Однородная линия имеет параметры    R₀ = 5 Ом / км,     С₀ = 5·10 ^-3 мкФ / км,     G₀ = 10 ^–6 См / км. При какой индуктивности в линии отсутствовали бы искажения?

     Ответ: L₀ = 25 мГн / км.

12. Определить, на каком минимальном расстоянии l должна быть закорочена линия без потерь с волновым сопротивлением R_С, чтобы ее входное сопротивление стало равным j R_С. Длина волны в линии.

     Ответ: l = λ / 8.