Запись математической модели сигнала в виде линейной комбинации функций Хевисайда, построение временного графика

Министерство общего и профессионального образования

Российской Федерации

Новосибирский государственный технический университет

Кафедра теоретических основ радиотехники

Расчетно-графическое задание №1

по курсу «Теория электрической связи» для студентов 2 – 3 курсов

специальностей 201200 и 201000 факультета РЭФ НГТУ

Факультет: РЭФ

Преподаватель: Тонконогов Е.А.

Студент: Гунзынов Б.У.

Группа: РКС10–71

Дата: _________________

Новосибирск 2009

Сигналы и их характеристики.

1.1.  Сигнал определяется восьмизначным равномерным кодом согласно варианту и подварианту, где символ «0» соответствует нулевой посылке, а символ «1» – прямоугольному видеоимпульсу напряжения с амплитудным значением 10 В и длительностью 0.1 мкс.

Вариант	Подвариант
	4
5	01001001

1.2.  Требуется:

Записать математическую модель сигнала в виде линейной комбинации функций Хевисайда, построить временной график.

Функция включения Хевисайда определяется выражением: 

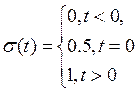                                                                                            (1.1)

Эффект скачка уровня при  описывается функцией  . Для того, чтобы импульс окончился при с, необходимо вычесть такой же импульс включения, запаздывающий на этот отрезок времени:  . Аналогично поступаем со вторым и третьим видеоимпульсами и окончательно получаем:

Построим временной график:

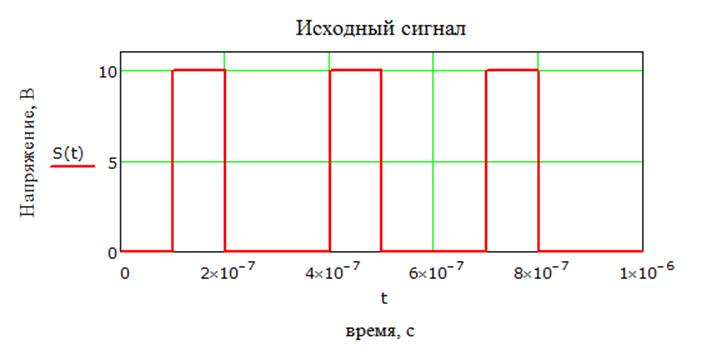
Рис 1.1

Найти спектр сигнала в базисе Уолша, построить спектральную диаграмму.

       Способ аналитического задания и нумерации (упорядочения) Функций Уолша может быть различным. Их можно сформировать, например, с помощью матриц Адамара. Матрицей Адамара  порядка  называется квадратная матрица размера  с элементами  такая, что

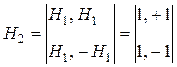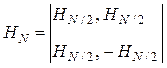                        , ,…, .                    (1.2)

ФУ, упорядоченные по Адамару ( с номером ), являются последовательностью прямоугольных импульсов с единичными амплитудами и полярностями, соответствующими знакам -й строки матрицы. Под длительностью подразумевается ()-я доля интервала ортогональности [0, T] или при введении безразмерного времени безразмерного интервала [0, 1].

Упорядочение по Уолшу характерно тем, что номер  функции  равен числу перемен знака на интервале ее существования (рис. 2.1).

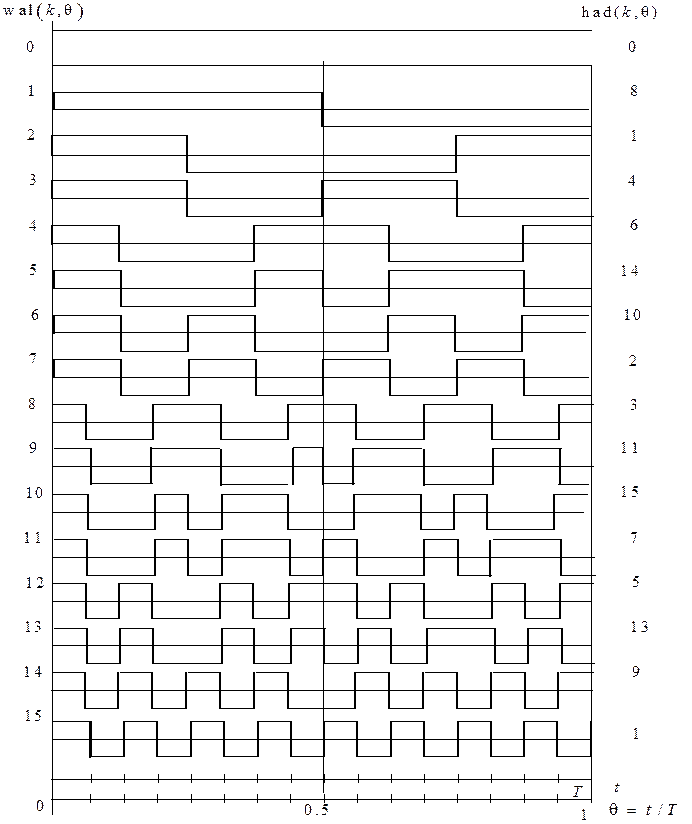
Рис 2.1 Функции Уолша

Спектральные коэффициенты Bn, представляющие собой проекции сигнала S(t) относительно базиса Уолша, определим из соотношения

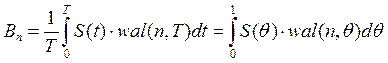                              ,                       (1.3)

где  интервал безразмерного времени, .

Построим исходный сигнал S(t) на интервале безразмерного времени

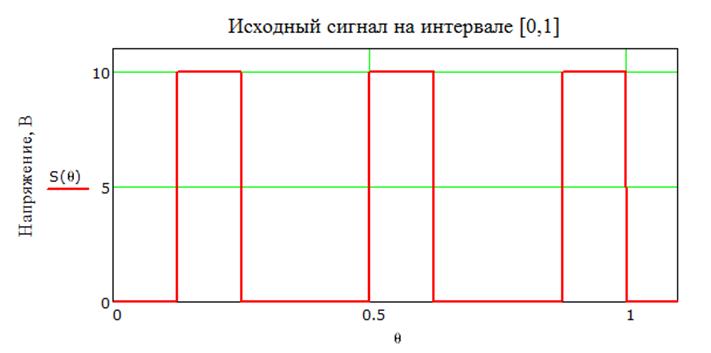
Рис 2.2

Вычислим спектральные коэффициенты Bn и построим спектральную диаграмму

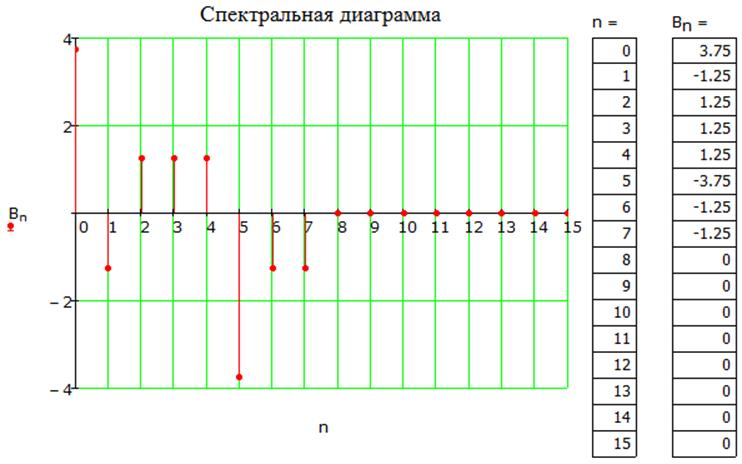
Рис 2.3

Найти аналитически спектральную плотность прямоугольного видеоимпульса относительно ядра Фурье.

Для того, чтобы перейти от временного описания сигнала s(t) к его описанию в частотной области S(ω) используют прямое преобразование Фурье:

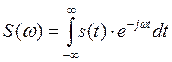                                                                                  (2.1)

Функция частоты  называется спектральной плотностью сигнала s(t).

Пусть данный сигнал s(t) имеет амплитуду U, длительность ти и располагается симметрично относительно начала отсчета времени. На основании формулы (2.1)

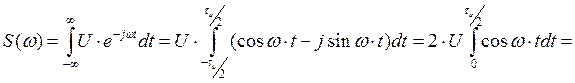
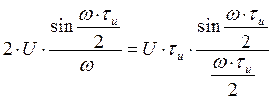
Спектральная плотность рассматриваемого сигнала s(t) есть вещественная функция частоты:

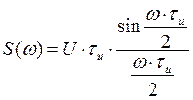
Пользуясь свойствами преобразования Фурье, найти спектральную плотность заданного сигнала относительно ядра Фурье, построить графики её модуля и аргумента.

Заданный сигнал S(t) представляет собой последовательность из трех одиночных прямоугольных видеоимпульсов смещенных во времени.

Найдём длительность и задержку исходного сигнала:

Длительность первого видеоимпульса: ,

Задержка: .

Длительность второго видеоимпульса: ,

Задержка: .

        Длительность третьего видеоимпульса: ,

        Задержка: .

Для описания спектральной плотности заданного сигнала S(t) воспользуемся двумя теоремами из свойств преобразования Фурье, а именно:

        Теоремой линейности:

                                                                              (3.1)

       Теоремой сдвига:

                                                                               (3.2)

Итак, спектральная плотность S(ω) заданного сигнала S(t) будет следующей:

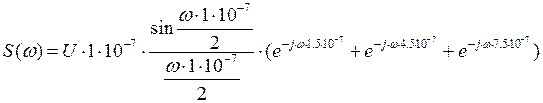
Построим графики модуля и аргумента спектральной плотности заданного