Частотные характеристики типовых линейных устойчивых звеньев систем автоматического управления

Министерство образования Российской Федерации

                     Новосибирский Государственный Технический Университет

                             Отчёт по лабораторной работе №2

«Частотные характеристики типовых линейных устойчивых звеньев систем автоматического управления»

Вариант:    2

Факультет: МТФ                                                          Преподаватель: Нос Олег Викторович

Группа:      КП-31

Студенты:    Кондратов А.С.

                        Гусев А. В.

                                                                    Новосибирск

2006

ЦЕЛЬ РАБОТЫ

Методом структурного моделирования снять и построить амплитудно-частотные характеристики типовых звеньев: апериодического, колебательного и реального дифференцирующего. Исследовать влияние параметров колебательного звена на вид амплитудно-частотной и фазочастотной характеристик.

АПЕРИОДИЧЕСОЕ ЗВЕНО

Исследуем методом структурного моделирования апериодическое звено с параметрами: К=4; T=0,25.

Полученные экспериментальные данные

w	0,4	1	2	3	4	10	20	30	40
T	15,7	6,28	3,14	2,09	1,57	0,628	0,314	0,209	0,157
A	0,995	0,9874	0,9806	0,8575	0,7071	0,53	0,2983	0,1543	0,0995
j	-5,71	-9,09	-11,31	-30,96	-45,00	-57,99	-72,64	-81,11	-84,31

Частотные характеристики

 

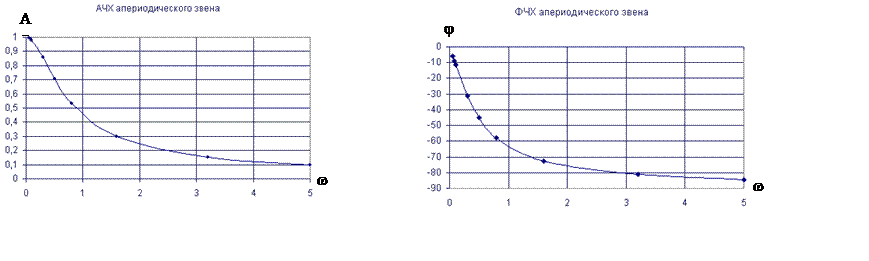
Вывод: в апериодическом звене при ω®0: A®k; φ®0˚, а при ω®È  A®0; φ®-90˚. На частоте сопряжения ω_ср=1/T=0,5 φ=-45˚.

КОЛЕБАТЕЛЬНОЕ ЗВЕНО

Исследуем методом структурного моделирования апериодическое звено с параметрами: k=2; T1=0,4; T1=0,7; ξ=0,5…1,5.

Полученные экспериментальные данные

при ξ = 0,5

ω	0	0.60	1.50	2.50	5.00	9.00	∞
A(ω)	2	1.93	1.62	1.14	0.43	0.14	0
φ(ω)	0	-24.06	-59.42	-90.35	-128.57	-149.14	-180

при ξ = 0,87

ω	0	0.60	1.50	2.50	5.00	9.00	∞
A(ω)	2	2.05	2.28	2.00	0.55	0.16	0
φ(ω)	0	-14.42	-42.00	-90.35	-143.43	-159.42	-180

при ξ = 1,5

ω	0	0.60	1.50	2.50	5.00	9.00	∞
A(ω)	2	1.68	1.04	0.66	0.30	0.13	0
φ(ω)	0	-37.47	-70.45	-90.35	-117.14	-131.83	-180

Частотные характеристики

при ξ = 0,5

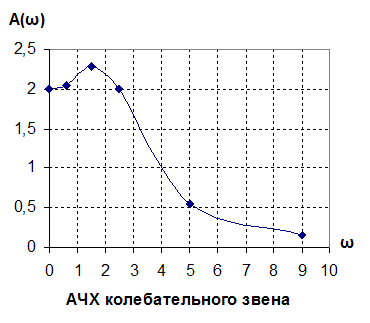
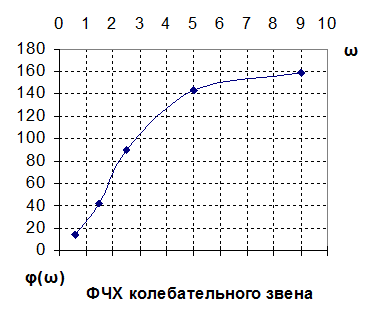
при ξ = 0,87

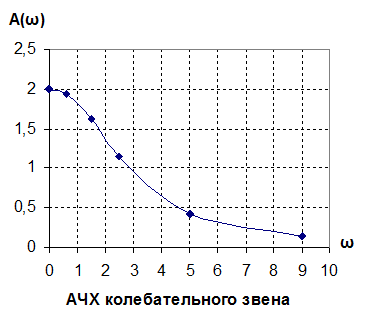
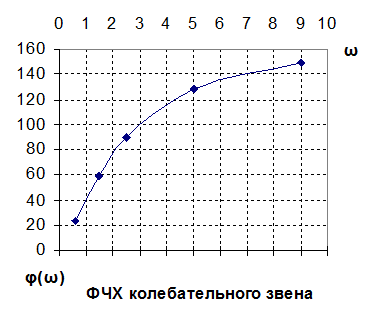
при ξ = 1,5

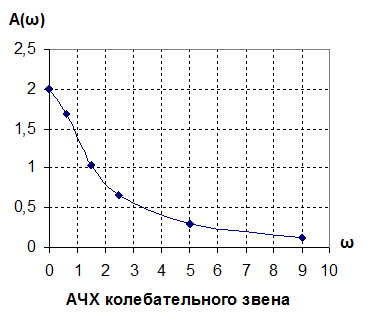
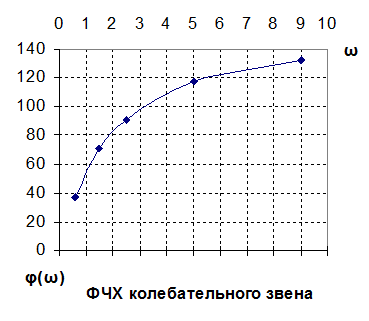
Вывод: в колебательном звене при ω=0: A(ω)=k; φ(ω)=0˚, а при ω=∞: A(ω)=0; φ(ω)=-180˚. На частоте сопряжения ω_ср=1/T₁=2.5 φ(ω)=-90˚. При коэффициенте демпфирования ξ<1 в области частоты сопряжения наблюдается скачок амплитудно-частотной характеристики выше значения k. Чем ниже коэффициент демпфирования, тем больше скачок.

                           РЕАЛЬНОЕ ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО

Исследуем методом структурного моделирования апериодическое звено с параметрами: k=1; T=0,08.

Полученные экспериментальные данные

ω	0	5	8	12.5	20	50	∞
A(ω)	0	3.53	5.65	8.83	14.14	35.35	20
φ(ω)	90	45.176	45.176	45.176	45.176	45.176	0

Частотные характеристики

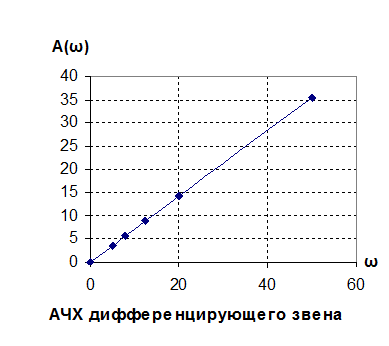
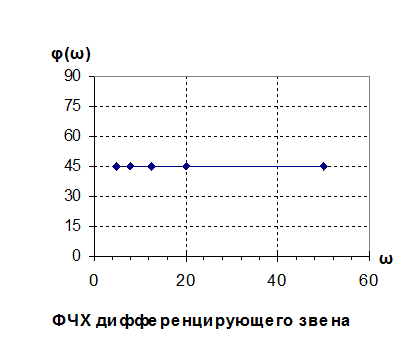
Вывод: в реальном дифференцирующем звене при ω=0: A(ω)=0; φ(ω)=90˚, а при ω=∞: A(ω)=k/T; φ(ω)=0˚. На частоте сопряжения ω_ср=1/T=12.5 φ(ω)=45˚.

ПРОВЕРКА РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ

1. Частотные характеристики апериодического звена при k=4; T=0.25; ω=4:

;

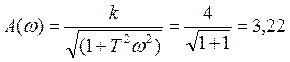ошибка при моделировании ;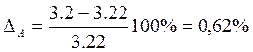

;

ошибка при моделировании .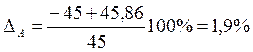

2. Частотные характеристики колебательного звена при k=2; T=0,4; ξ=0,87; ω=2.5:

;

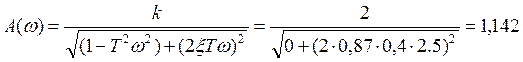ошибка при моделировании ;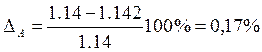

;

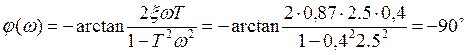ошибка при моделировании .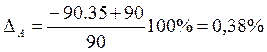

3. Частотные характеристики дифференцирующего звена при k=1; T=0,08; ω=12.5:

;

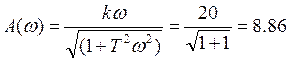ошибка при моделировании ;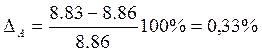

;

ошибка при моделировании .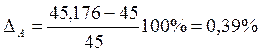

Выводы

Все частотные характеристики типовых линейных звеньев, снятые с помощью структурного моделирования в программе «MATLAB 6.5 - SIMULINK», совпадают с характеристиками, полученными в результате аналитического исследования этих звеньев.