



НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра АППМ
Отчет по лабораторной работе
Дисциплина:‹‹Теория автоматического управления»
Работа №2
Наименование: Частотные характеристики типовых линейных динамических звеньев и линейной САУ в разомкнутом состоянии
Группа КП-501
Вариант № 4
1.Горбачевский Виталий
2. Кожемяко Ирина
Работа защищена:
Преподаватель: Нос О. В.
Новосибирск
2008 г.
Целью работы является исследование с помощью метода цифрового моделирования частотных характеристик типовых линейных динамических звеньев в обычном и логарифмическом масштабах, а также построение логарифмических АЧХ и ФЧХ одномерных линейных САУ в разомкнутом состоянии.
|
k |
T |
ξ |
k1 |
T1 |
|
4.5 |
2.5 |
0.75 |
2.5 |
0.5 |
Где T- постоянная времени, K- коэффициент передачи, ξ- коэффициент демпфирования.
2.1 Интегрирующее звено
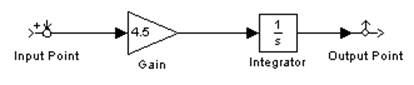
2.1.1 Построить АЧХ интегрирующего звена в обычном и логарифмическом
масштабах.
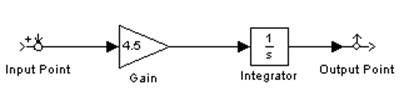
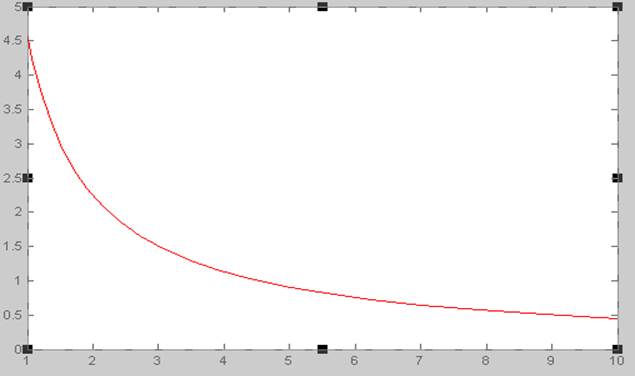
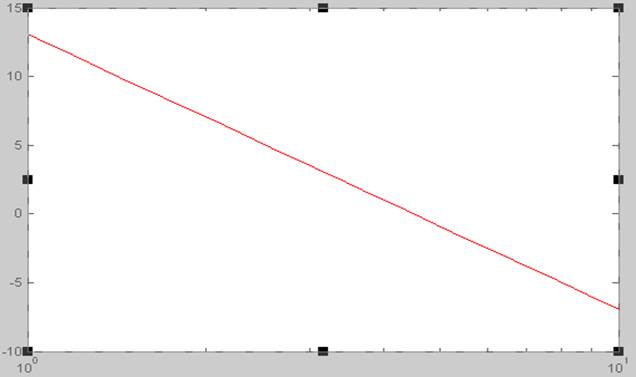
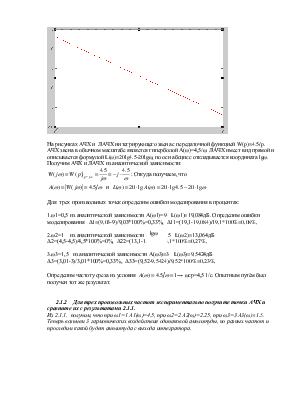
На рисунках АЧХ и ЛАЧХ интегрирующего звена с передаточной функцией W(p)=4.5/p.
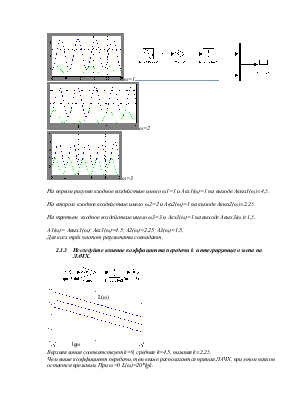
АЧХ звена в обычном масштабе является гиперболой А(ω)=4,5/ω. ЛАЧХ имеет вид прямой и описывается формулой L(ω)=20lg4.5-20lgω, по оси абсцисс откладывается координата lgω.
Получим АЧХ и ЛАЧХ из аналитической зависимости:
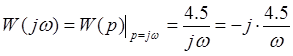 ; Откуда
получаем, что
; Откуда
получаем, что
![]() и
и ![]()
|
|
1.ω1=0,5 из аналитической зависимости А(ω1)=9 L(ω1)=19,084дБ. Определим ошибки моделирования Δ1=(9,03-9)/9,03*100%=0,33%, Δ11=(19,1-19,084)/19,1*100%=0,08%,
2.ω2=1 из аналитической зависимости А(ω2)=4.5 L(ω2)=13,064дБ
Δ2=(4,5-4,5)/4,5*100%=0%, Δ22=(13,1-13,064)/13,1*100%=0,27%,
3.ω3=1,5 из аналитической зависимости А(ω3)=3 L(ω3)=9,5424дБ
Δ3=(3,01-3)/3,01*100%=0,33%, Δ33=(9,52-9,5424)/9,52*100%=0,23%,
Определим частоту среза из условия ![]() →
ωср=4,5 1/с. Опытным путём был получен тот же результат.
→
ωср=4,5 1/с. Опытным путём был получен тот же результат.
|
||||
|
||||
2.1.2 Для трех произвольных частот экспериментально получите точки АЧХ и
сравните их с результатами 2.1.1.
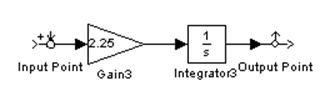
Из 2.1.1. получим, что при ω1=1 А1(ω)=4.5, при ω2=2 А2(ω)=2.25, при ω3=3 А3(ω)=1.5.
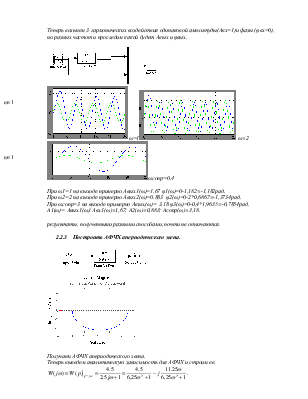
Теперь возьмем 3 гармонических воздействия одинаковой амплитуды, но разных частот и
проследим какой будет амплитуда с выхода интегратора.
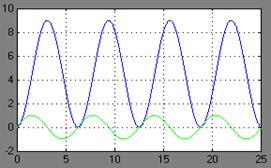 ω=1
ω=1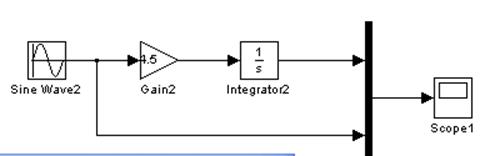
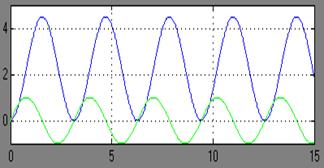 ω=2
ω=2
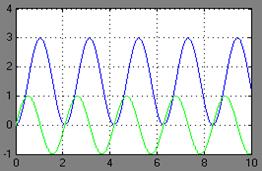 ω=3
ω=3
На первом рисунке входное воздействие имело ω1=1 и Авх1(ω)=1 на выходе Авых1(ω)=4,5.
На втором входное воздействие имело ω2=2 и Авх2(ω)=1 на выходе Авых2(ω)=2,25.
На третьем входное воздействие имело ω3=3 и Авх3(ω)=1 на выходе Авых3(ω)=1,5.
A1(ω)= Авых1(ω)/ Авх1(ω)=4.5; A2(ω)=2.25; A3(ω)=1.5.
Для всех трёх частот результаты совпадают.
2.1.3 Исследуйте влияние коэффициента передачи k интегрирующего звена на ЛАЧХ.
|
|
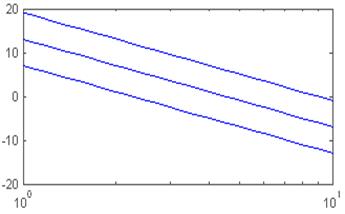
Верхняя линия соответствует k=9, средняя k=4.5, нижняя k=2.25.
Чем выше коэффициент передачи, тем выше располагается прямая ЛАЧХ, при этом наклон остается прежним. При ω=0 L(ω)=20*lgk.
2.2 Апериодическое звено.
2.2.1 Постройте АЧХ и ФЧХ апериодического звена с коэффициентом передачи k,
постоянной времени T в обычном и логарифмическом масштабах.
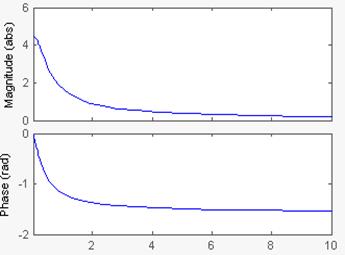
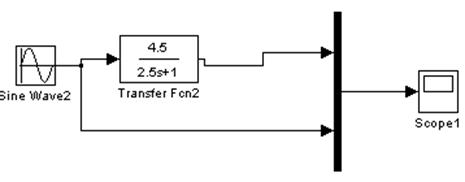
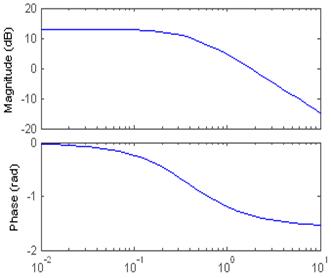
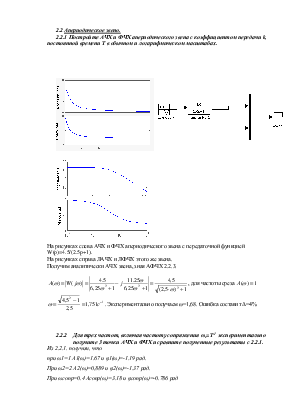
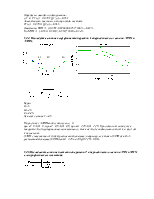
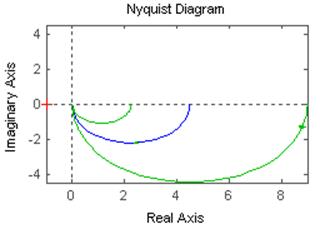
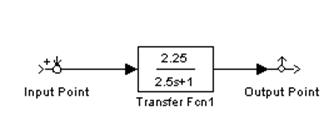
На рисунках слева АЧХ и ФЧХ апериодического звена с передаточной функцией W(p)=4.5/(2.5p+1).
На рисунках справа ЛАЧХ и ЛФЧХ этого же звена.
Получим аналитически АЧХ звена, зная АФЧХ 2.2.3.
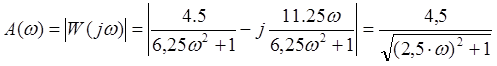 , для частоты
среза
, для частоты
среза ![]()
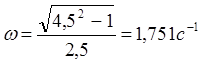 . Экспериментально получаем
ω=1,68. Ошибка составит Δ=4%
. Экспериментально получаем
ω=1,68. Ошибка составит Δ=4%
2.2.2 Для трех частот, включая частоту сопряжения ωc=T-1 экспериментально получите 3 точки АЧХ и ФЧХ и сравните полученные результаты с 2.2.1.
Из 2.2.1. получим, что
при ω1=1 А1(ω)=1.67 и φ1(ω)=-1.19 рад.
При ω2=2 А2(ω)=0,889 и φ2(ω)=-1.37 рад.
При ωсопр=0.4 Асопр(ω)=3.18 и φсопр(ω)=-0.786 рад
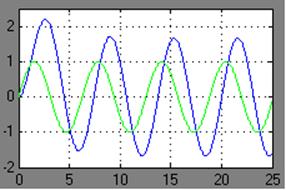
Теперь возьмем 3 гармонических воздействия одинаковой амплитуды(Авх=1)и фазы (φвх=0), но разных частот и проследим какой будет Авых и φвых.
 ω=1
ω=1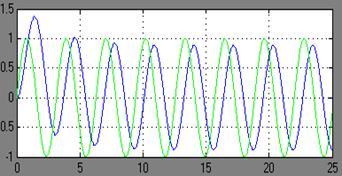 ω
ω
|
|
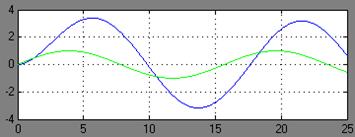 ωсопр=0.4
ωсопр=0.4
При ω1=1 на выходе примерно Авых1(ω)=1.67 φ1(ω)=0-1,182=-1,182рад.
При ω2=2 на выходе примерно Авых2(ω)=0.883 φ2(ω)=0-2*0,6867=-1,3734рад.
При ωсопр=3 на выходе примерно Авых.(ω)= 3.18 φ3(ω)=0-0,4*1,9635=-0,7854рад.
A1(ω)= Авых1(ω)/ Авх1(ω)=1,67; A2(ω)=0,883; Aсопр(ω)=3,18.
результаты, полученными разными способами, почти не отличаются.
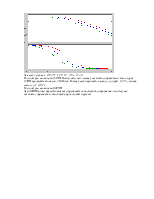
2.2.3 Построить АФЧХ апериодического звена.
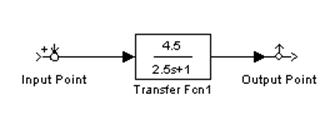
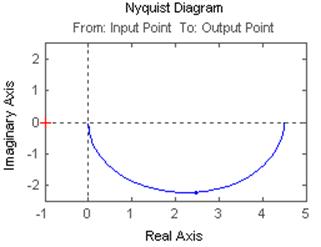
Получаем АФЧХ апериодического звена.
Теперь выведем аналитическую зависимость для АФЧХ и строим ее.
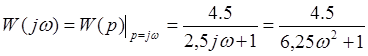
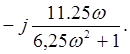
Определим ошибку моделирования.
ω1=3 P1(ω)= 0.0791 Q1(ω)=-0.591
Аналитически получаем, что при этой частоте
P1(ω)= 0,0786 Q1(ω)=-0,589
Ошибка по ВЧХ Δ=(0,0791-0,0786)/0,0791*100% =0,63%
По МЧХ Δ=(-0,591+0,589)/(-0,591)*100%=0,34%
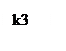
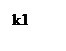
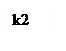
 2.2.4.
Исследуйте влияние коэффициента передачи k
апериодического звена на ЛАЧХ и АФЧХ.
2.2.4.
Исследуйте влияние коэффициента передачи k
апериодического звена на ЛАЧХ и АФЧХ.
Берем
k1=9
k2=4,5
k3=2,25.
Для всех случаев T=2.5
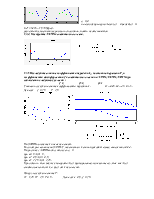
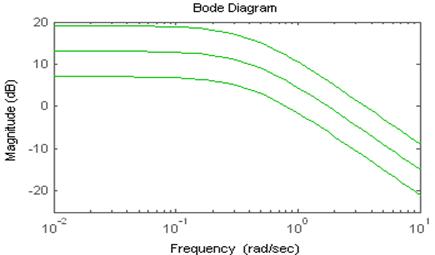
На рисунке с АФЧХ видно, что если ω=0,
при к1=9 А(0)=9, при к2=4,5 А(0)=4,5, при к3=2,25 А(0)=2,25. При одном и том же угле поворота А(ω) пропорционально увеличилась, так как А(ω) линейно зависит от k, а φ(ω) от k не зависит.
ЛАЧХ с увеличением k будет располагаться выше, например, все точки ЛАЧХ для k1=9 располагаются выше ЛАЧХ для k3=2,25 на 20lg(9/2,25)≈12дБ.
2.2.5.Исследовать влияние постоянной времени Т апериодического звена на АЧХ и ФЧХ в логарифмическом масштабе.
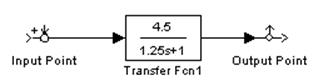
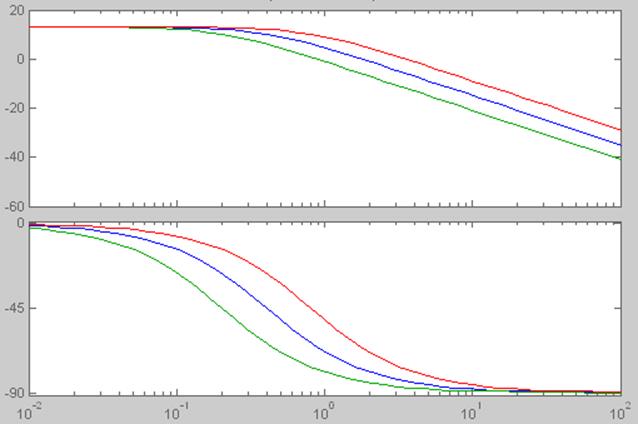
Для всех случаев к=4.5, Т1=1,25 T2=2,5 и T3=5.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.