Рассмотрим влияние на ЛАЧХ. Видно, что чем меньше частота сопряжения, тем скорее ЛАЧХ приобретет наклон -20дБ/дек. Раньше всех перегнется звено с ωсопр3=0,2 1/с, позже звено с ω1=0,8 1/с.
Рассмотрим влияние на ЛФЧХ.
Для ЛФЧХ точка перегиба также определяется частотой сопряжения, чем больше частота сопряжения, тем позже происходит перегиб.
2.3 Колебательное звено.
2.3.1. Постройте АЧХ, ЛАЧХ, ФЧХ, ЛФЧХ для случая колебательного звена с коэффициентом передачи k1, постоянной времени Т1 и коэффициентом демпфирования ξ .
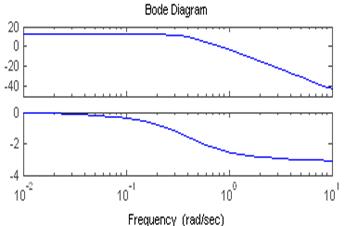
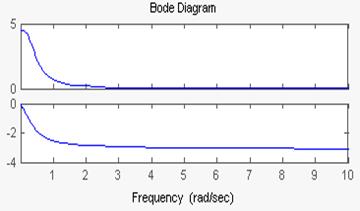
Передаточная функция этого звена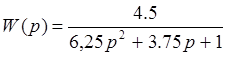 
ξ=0,75,
к=4,5, Т=2,5
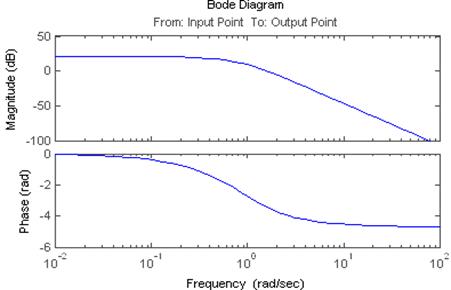
Слева представлены ЛАЧХ и ЛФЧХ, справа- АЧХ и ФЧХ.
2.3.2. По полученной АЧХ получить параметры частотной характеристики.
1. Определим показатель колебательности Аmax(ω)=4.5 А(0)=4,5 М=4,5/4,5=1
2. Определим частоту среза: L(ωср)=0 → ωср=0,825 1/с
3.Полоса пропускания: 
→
полоса пропускания (0;0,376)
4. Резонансная частота ωрез=0 1/с.
2.3.3. Для трех частот, включая частоту сопряжения , экспериментально получите три точки АЧХ и ФЧХ и сравните полученные результаты с с 2.3.1.
Из 2.3.1. получим, что
при ω1=1 А1(ω)=0,712 и φ1(ω)= -2,52рад.
При ω2=2 А2(ω)=0,182 и φ2(ω)= -2,84рад.
При ωсопр=0.4 Асопр(ω)=3 и φсопр(ω)=-1,57 рад
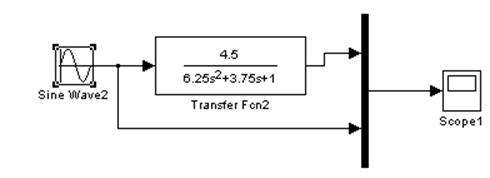
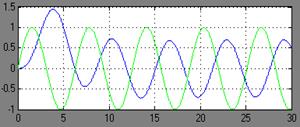Теперь возьмем 3 гармонических воздействия одинаковой
амплитуды(Авх=1)и фазы (φвх=0), но разных частот и проследим какой будет Авых и
φвых.
ω=1
на выходе примерно Авых1(ω)=0,6973
φ1(ω)=0-2,5205=-2,5205рад.
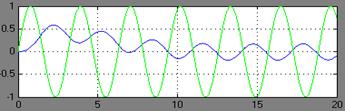
ω=2
на выходе примерно Авых2(ω)=0,1727 φ2(ω)=0-2*0,6867=-2,8824рад.
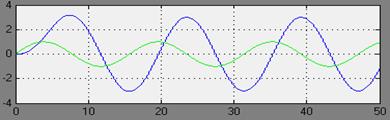
ω=0,4
на выходе примерно Авых.(ω)=
3 φвых3(ω)=0-0,4*3,9271=-1,57084рад.
результаты, полученные разными способами, почти не отличаются.
2.3.4. Постройте АФЧХ колебательного звена.
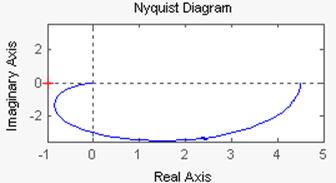
2.3.5 Исследуйте влияние коэффициента передачи k1, постоянной времени T1 и коэффициента демпфирования ξ колебательного звена на ЛАЧХ, ЛФЧХ, АФЧХ при соблюдении следующих условий :
ξ=1, ξ>1, ξ<1
Сначала исследуем влияние коэффициента передачи k. k1=2.25, k2=4,5, k3=9.
Для всех ξ=0,75 Т=2,5
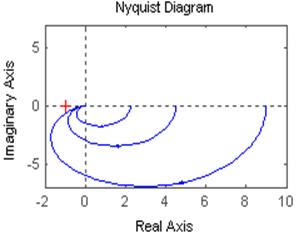
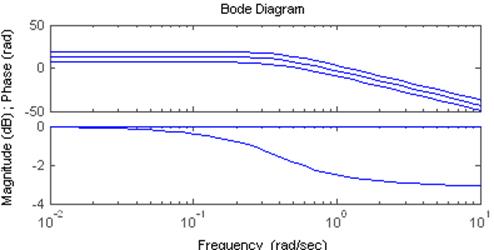
На ЛФЧХ изменение k никак не влияет.
Рассмотрим влияние на ЛАЧХ. С увеличением k линии проходят выше, аналогично 2.2.4.
На рисунке с АФЧХ видно, что если ω=0
при к3=9 А(0)=9,
при к2=4,5 А(0)=4,5,
при к1=2,25 А(0)=2,25.
При одном и том же угле поворота А(ω) пропорционально увеличилась, так как А(ω) линейно зависит от k, а φ(ω) от k не зависит.
Теперь исследуем влияние Т:
T1=1,25 Т2=2,5 Т3=5. Для всех к=4,5, ξ=0,75.
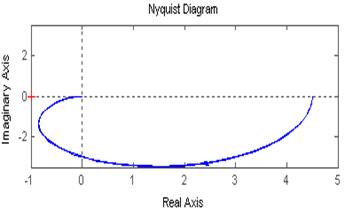
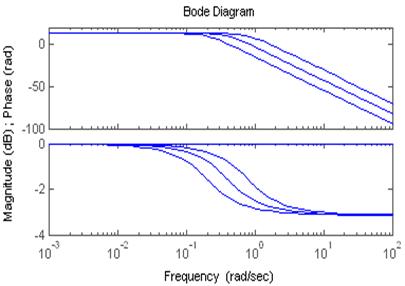
Рассмотрим влияние на ЛАЧХ.
Видно, что чем меньше частота сопряжения, тем скорее ЛАЧХ приобретет наклон -20дБ/дек. Раньше всех перегнется звено с ωсопр3=0,2 1/с, позже звено с ω1=0,8 1/с.
Рассмотрим влияние на ЛФЧХ.
Для ЛФЧХ точка перегиба также определяется частотой сопряжения, чем больше частота сопряжения, тем позже происходит перегиб.
АФЧХ для трех значений Т сливаются, но одна и та же точка на АФЧХ соответствует трем разным частотам для трех разных Т, так как ВЧХ и МЧХ зависят от Т*ω. Следовательно для достижения определенного значения МЧХ и ВЧХ при большем Т требуется меньшее ω.
Исследуем влияние ξ:
ξ1=0,75, ξ2=1, ξ3=1,5. k=4.5 T=2.5
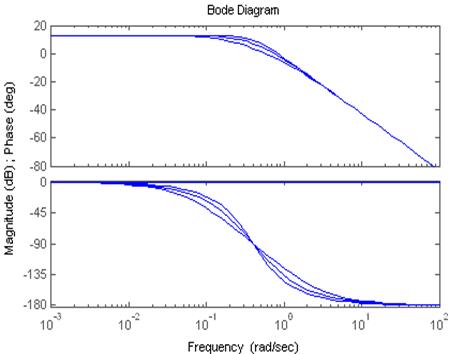
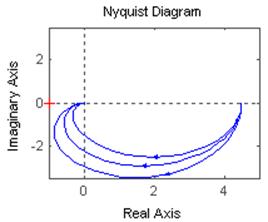
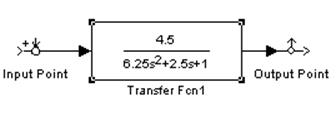
Влияние на ЛФЧХ.
Чем больше ξ, тем меньшее требуется ω для достижения определенного уровня φ(ω)-до перегиба, а после- наоборот.
Влияние на ЛАЧХ.
Чем больше ξ, тем более плавно проходит кривая ЛАЧХ и тем меньше значения L(ω) около частот сопряжения.
Чем меньше ξ, тем большие по модулю значения способны принимать МЧХ и ВЧХ.
2.4. Частотные характеристики в логарифмическом масштабе линейной одномерной непрерывной линейной САУ в разомкнутом состоянии.
2.4.1 Получите АЧХ и ФЧХ в логарифмическом масштабе при последовательном соединении типовых интегрирующего и колебательного звеньев.
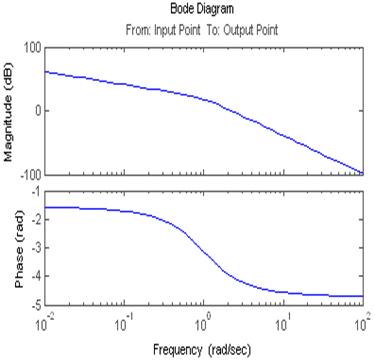
Для интегрирующего звена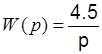 
, колебательного-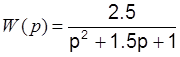 
Построим ЛАЧХ.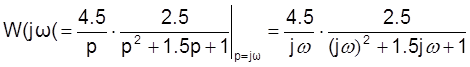
.
.
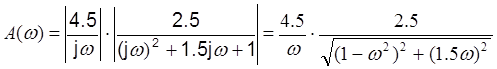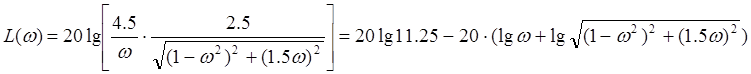
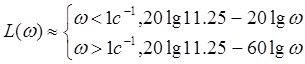
Из этой зависимости получим ωсопр=1 L(ωсопр)=21.023дБ
Экспериментально L(ωсопр)=17,5. Ошибка составляет Δ=(21,023-17,5)/21,023*100%=16,75%
2.4.2. Постройте ЛАЧХ и ЛФЧХ последовательно соединенных типовых апериодического и колебательного динамических звеньев.
Для апериодического звена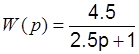 
,
Построим ЛАЧХ.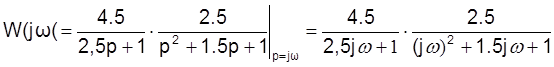
.
.
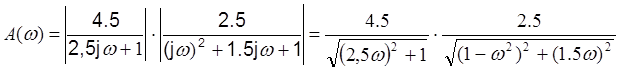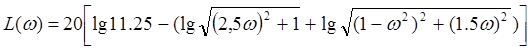
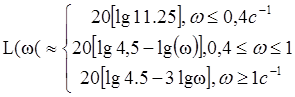
Из этой зависимости получим ωсопр1=0.4 L(ωсопр1)=21.023дБ; ωсопр2=1 L(ωсопр2)=13.064дБ;
Экспериментально L(ωсопр1)=17,7. Ошибка составляет Δ=(21,023-17.7)/21,023*100%≈16%
L(ωсопр2)=8.74. Ошибка составляет Δ=(13.064-8.74)/13.064*100%=33%
2.4.3. Исследуйте влияние коэффициента передачи САУ в разомкнутом состоянии Краз, а так же постоянных времени апериодического и колебательного звеньев на ЛАЧХ и ЛФЧХ для пункта 2.4.2.
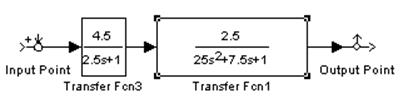
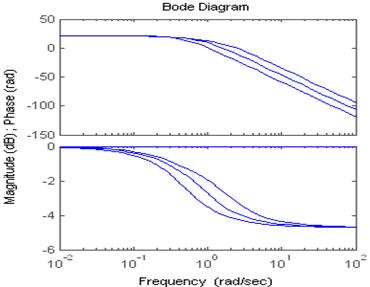
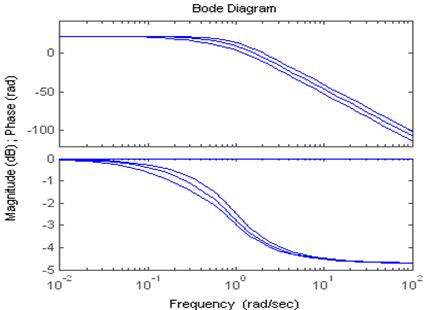
Для рисунков слева меняемТ для апериодического звена,
справа- колебательного.
1.Изменяем Т для апериодического звена: Т1=2,5, Т2=1,25, Т3=5.
С изменением Т меняется частота сопряжения апериодического звена - для больших Т она меньше. Изменяется наклон между частотами сопряжения, который определяется в основном Т апериодического звена, так как ωсопр этого звена для всех случаев меньше ωсопр колебательного звена.
2. Изменяем Т для колебательного звена: Т1=1, Т2=0,5, Т3=2. Изменяется частота сопряжения колебательного звена. Здесь для трех случаев ωсопр этого звена всегда меньше ωсопр апериодического звена и, следовательно, наклон между двумя этими частотами определяется Т колебательного звена.
ЛФЧХ в этих случаях складываются перегибы наблюдаются в φ(ω)=135гр.
Теперь коэффициент передачи:
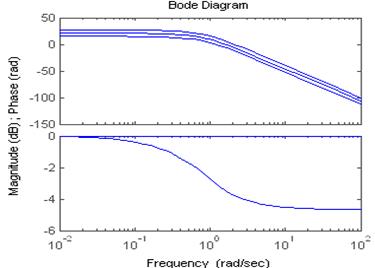k1=11.25; k2=22.5; k3=5.625
Изменение k никак не влияет на ЛФЧХ, но с увеличением k линии ЛАЧХ проходят выше.
При ω=0 L(ω)=20*lgk.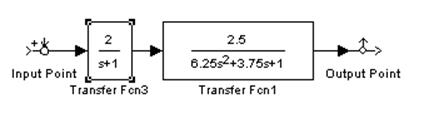
Вывод: на лабораторной работе мы исследовали с помощью метода цифрового моделирования частотные характеристики типовых линейных динамических звеньев в обычном и логарифмическом масштабах, а также строили ЛАЧХ и ЛФЧХ одномерных линейных САУ в разомкнутом состоянии.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.