Типовые звенья линейных САР. Апериодическое звено и инерционно-дифференцирующее звено первого порядка. Типовые звенья линейных САР. Форсирующие звенья первого и второго порядка

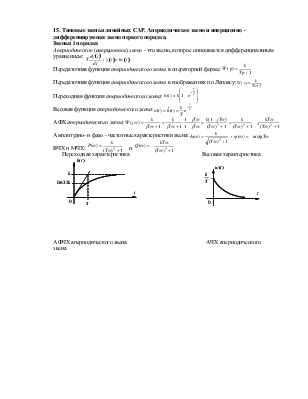
15. Типовые звенья линейных САР. Апериодическое звено и инерционно - дифференцирующее звено первого порядка.

Звенья I порядка

Апериодическое (инерционное) звено - это звено, которое описывается дифференциальным уравнением:

 

Передаточная функция апериодического звена в операторной форме:

 

Передаточная функция апериодического звена в изображениях по Лапласу:

 

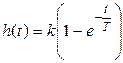Переходная функция апериодического звена:

 

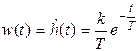Весовая функция апериодического звена:

 

АФХ апериодического звена:

 

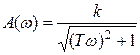Амплитудно- и фазо - частотные характеристики звена:                              ,

 

ВЧХ и МЧХ:                               и

      Переходная характеристика                                                   Весовая характеристика

                                                 

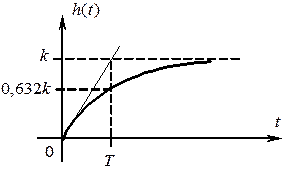
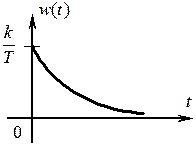
АФЧХ апериодического звена                                                        АЧХ апериодического звена

                  

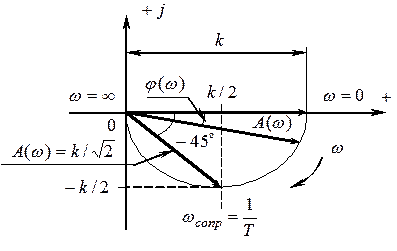
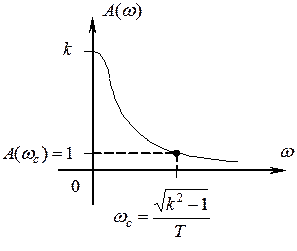
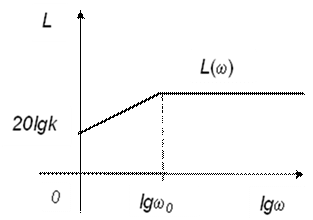
ЛАЧХ звена описывается выражением:

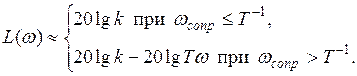
ЛАЧХ звена можно с достаточной степенью точности аппроксимировать с помощью двух асимптотических прямых, которые соединяются на частоте сопряжения                    :

Максимальное отклонение асимптотической ЛАЧХ от точной, которое имеет место на частоте

                   , определяется в соответствии с равенством                           и составляет 3,01 дБ.

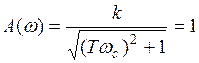На частотах              наклон ЛАЧХ составляет –20 дБ/дек, а частота среза определяется на основании

 

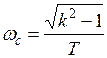равенства                                             откуда

Точные и асимптотические АЧХ, а также ФЧХ в логарифмическом масштабе

Инерционно - дифференцирующее звено первого порядка описывается следующим дифференциальным уравнением:

 

Передаточная функция звена в операторной форме:

 

Передаточная функция звена в изображениях по Лапласу:

 

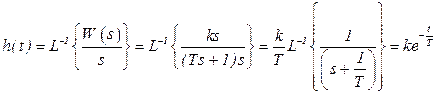Переходная функция звена:

 

Весовая функция звена:

 

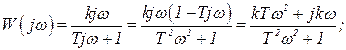АФХ звена:                                                                 или

 

Амплитудно- и фазо - частотные характеристики звена:                              ,

 

ВЧХ и МЧХ:                              и

ЛАЧХ звена описывается выражением:

 

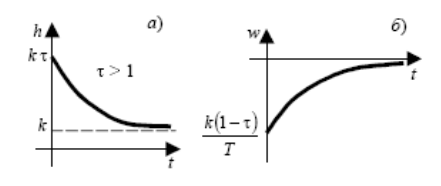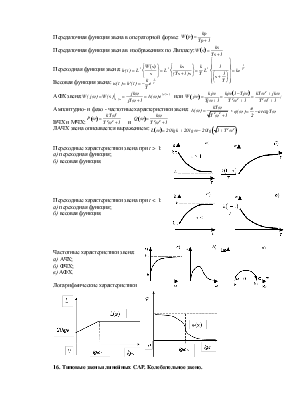
Переходные характеристики звена при t > 1:

а) переходная функция;

б) весовая функция.

 

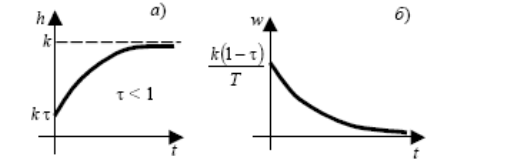Переходные характеристики звена при t < 1:

а) переходная функция;

б) весовая функция.

 

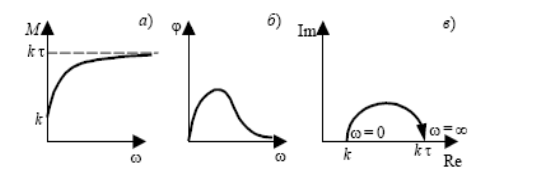Частотные характеристики звена:

а) АЧХ;

б) ФЧХ;

в) АФХ.

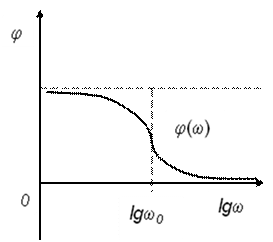
Логарифмические характеристики звена

16. Типовые звенья линейных САР. Колебательное звено.

Звенья IIпорядка

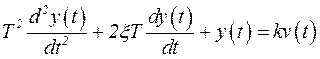Колебательное звено – это звено описывается следующим дифференциальным уравнением:

                                                                                                                 ,

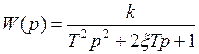где ξ  - коэффициент демпфирования (затухания), влияющий на степень колебательности переходного процесса.

Передаточная функция звена в операторной форме:

 

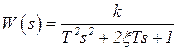Передаточная функция звена в изображениях по Лапласу:

 

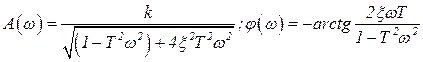Амплитудно-  и фазо - частотная характеристики:

 

Характеристическое уравнение                                            в зависимости от значения ξ имеет три вида корней. Вследствие этого свойства данного звена изменяются настолько существенно, что

при различных значениях ξ это звено имеет различные названия:

•     консервативное;

•     колебательное;

•     апериодическое звено второго порядка.

1. Консервативное звено: ξ = 0. При этом ее полюса чисто мнимые:

 

Передаточная функция в операторной форме:

 

Переходная функция звена:

 

Весовая функция звена:

 

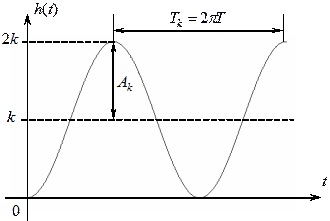На выходе консервативного звена

при единичном ступенчатом входном воздействии

присутствуют незатухающие гармонические колебания

со следующими параметрами:

•    амплитуда колебаний, смещенных

по оси ординат на величину k: A_k = k;

•    период колебаний: T_k = 2pT;

•    частота собственных незатухающих

              колебаний: w₀ = T^-1.

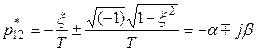2. Колебательное звено: 0 < ξ < 1.

Полюса передаточной функции – комплексно-сопряженные числа:

 

Здесь                ,                           – соответственно вещественная и мнимая части корней D(p).

 

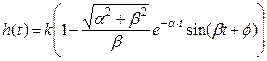Переходная функция звена:

 

Весовая функция звена:

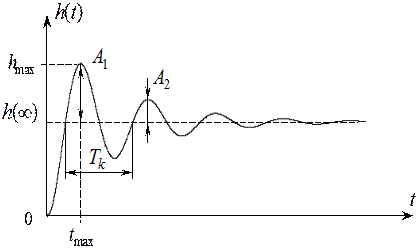Переходная характеристика колебательного звена при ξ < 1 представляет собой затухающие гармонические колебания, период которых зависит

от мнимой составляющей корней β,

а степень демпфирования амплитуды

от вещественной части α.

Согласно графику h(t):

 

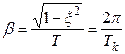Частота собственных затухающих колебаний:

 

С течением времени значения характеристик стремятся к величине коэффициентов усиления звеньев.

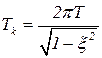При ξ > 1 колебательность переходной функции исчезает и она становится монотонной. Постоянная времени Т  колебательного звена не равна периоду колебаний Т_k:

При ξ < 0,5 период затухающих колебаний равен примерно Т_k ≈ 2 π Т.

По колебательной переходной характеристике колебательного звена  при ξ < 0,5 можно приближенно оценить его параметры:

•   уровень успокоения колебаний равен коэффициенту усиления звена;