Типовые звенья линейных САР. Апериодическое звено и инерционно-дифференцирующее звено первого порядка. Типовые звенья линейных САР. Форсирующие звенья первого и второго порядка, страница 2

•   постоянная времени равна Т _k ≈  Т/2π;

•   декремент затухания  χ  ≈  3Т/Т_пер.

Длительность переходного процесса Т_пер колебательного звена составляет:

Ø  при ξ < 0,5 равна 3Т/ ξ;

Ø  при ξ > 1 она составляет 6 ξ Т.

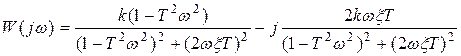При ξ = 0,707 длительность переходного процесса минимальна и составляет 2,3Т.

АЧХ колебательного звена:

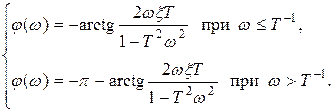Амплитудно- и фазо - частотные характеристики звена:

 

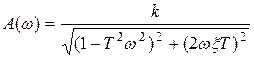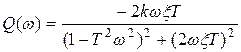
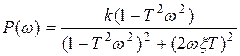ВЧХ и МЧХ:

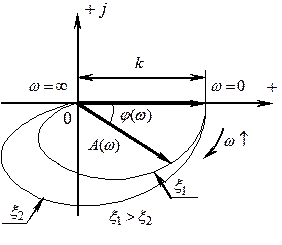АФЧХ колебательного звена

17. Типовые звенья линейных САР. Форсирующие звенья первого и  второго порядка.

Форсирующее (дифференцирующее) звено первого порядка описывается следующим

 

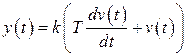дифференциальным уравнением:

 

Передаточная функция форсирующего звена в операторной форме:

Передаточная функция форсирующего звена в изображениях по Лапласу:

Переходная функция форсирующего звена:

Весовая функция форсирующего звена:

АФХ форсирующего звена:

Амплитудно- и фазо - частотные характеристики звена:                              ,

ВЧХ и МЧХ:                 и

ЛАЧХ звена описывается выражением:

АФЧХ форсирующего звена первого порядка               ЛАЧХ и ЛФЧХ форсирующего звена первого порядка

                                    

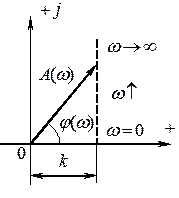
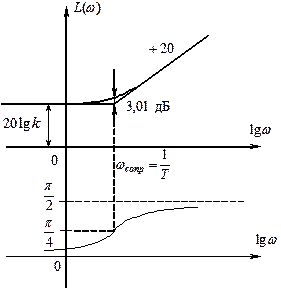
Форсирующее (дифференцирующее) звено второго порядка  описывается дифференциальным

 

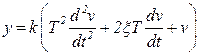уравнением вида:

                                                                                                                 

Переходная функция звена:

Весовая функция звена:

Передаточная функция звена в операторной форме:

Передаточная функция звена в изображениях по Лапласу:

Амплитудно-  и фазо - частотная характеристики:

 

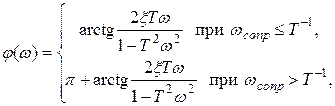ВЧХ и МЧХ:

ЛАЧХ:

В случае асимптотических прямых при выполнении условий T²ω² >> 1  и T²w² >> 2ξ  по аналогии с колебательным звеном:

При этом необходимо помнить, что если коэффициент демпфирования находится вне диапазона

                , то при построении асимптотических ЛАЧХ вблизи частоты сопряжения необходимо уточнять частотную характеристику путем использования специальных корректирующих номограмм.

              

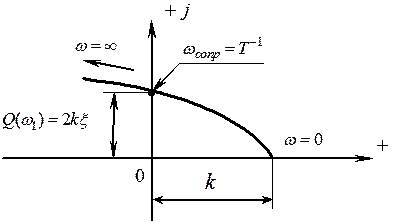
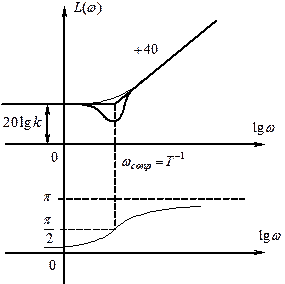
АФЧХ форсирующего звена второго                   ЛАЧХ и ЛФЧХ форсирующего звена второго

                             порядка                                                                       порядка

18. Построение ЛАЧХ и ЛФЧХ одноконтурных систем.

Передаточная функция одноконтурной разомкнутой системы:

 

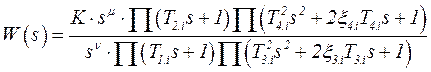Здесь n, μ - количество интегрирующих и дифференцирующих звеньев соответственно;

T_1.i, T_2.i - постоянные времени инерционных и форсирующих звеньев первого порядка соответственно;

T_3.i, T_4.i - постоянные времени для звеньев второго порядка соответственно;

ξ_3.i, ξ_4.i - степени затухания звеньев второго порядка инерционного и форсирующего типа.

Правила построения ЛАЧХ одноконтурной САР

1. Определяют 20lgK сопрягающие частоты w_i = 1/Т_i.

2. В прямоугольной системе координат по горизонтальной оси в логарифмическом масштабе откладываем сопрягающие частоты, а по вертикальной оси при w = 1 откладываем 20lgK.

3. Строим низкочастотную асимптоту (НЧ – асимптоту), представляющую собой полупрямую в диапазоне частот от w = 0 до наименьшей сопрягающей частоты с наклоном: - 20(ν - μ) дБ/дек. Эта асимптота (или ее продолжение, если наименьшая сопрягающая частота меньше 1) проходит через точку w = 1, L = 20lgK.

4. При возрастании w строим асимптотическую ЛАЧХ как ломаную линию, прямолинейные отрезки которой изменяют свой наклон при сопрягающих частотах wi следующим образом:

•     на  - 20дб/дек, если сопрягающая частота принадлежит апериодическому звену;

•     на  - 40 дб/дек – если колебательному звену;

•     на  + 20дб/дек – если дифференцирующему звену 1-го порядка;

•     на  + 40дб/дек – если дифференцирующему звену 2-го порядка.

5. Уточняют вид ЛАЧХ при ξ < 0,38 или 0,7 < ξ < 1 добавлением поправки, если звено инерционное, вычитанием поправки, если звено форсирующее. Корректировку проводят в окрестности соответствующей сопрягающей частоты w_i.

Определение . Частота, при которой ЛАЧХ пересекает ось частот, называют частотой среза w_с, L(w_с) = 0.

Построенная таким образом ЛАЧХ относится к числу типовых (желаемых), т.к. обеспечивает достаточно высокую устойчивость и хорошие показатели качества переходных процессов благодаря минимальному наклону вблизи частоты среза и достаточной протяженности прилегающего к этой частоте участка.

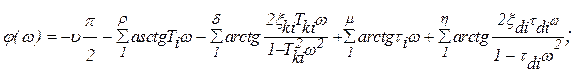ЛФЧХ строится по соотношению:

ЛФЧХ одноконтурной системы может быть также получена суммированием ординаты ЛФЧХ типовых звеньев.

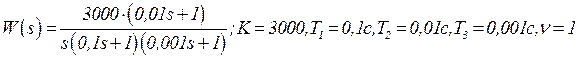Рассмотрим некоторую разомкнутую САР с передаточной функцией следующего вида:

 

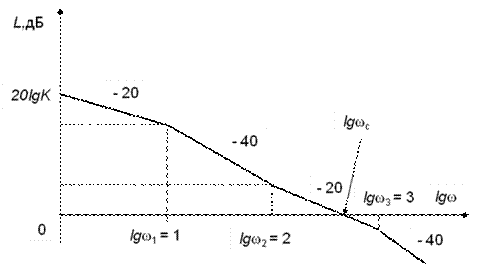
Построить асимптотическую ЛАЧХ системы в разомкнутом состоянии, причем T₂ > T₃и ξ₂ = 1.

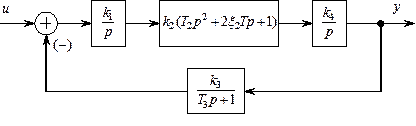
Наклон низкочастотной асимптотической прямой определяется двумя интегрирующими звеньями с общим коэффициентом передачи                          .

 

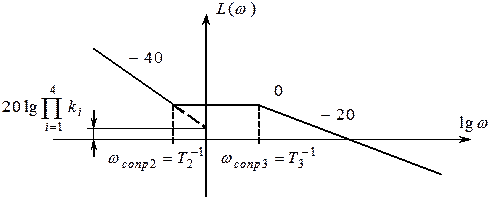
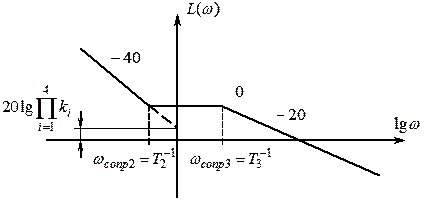На частоте сопряжения                      у форсирующего звена второго порядка изменяется наклон асимптоты на +40 дБ/дек, вследствие чего ЛАЧХ системы в разомкнутом состоянии становится параллельной оси абсцисс.

При дальнейшем увеличении частоты и достижении значения                     происходит изменение наклона асимптотической прямой ЛАЧХ апериодического звена и               ослабляется на –20 дБ/дек.

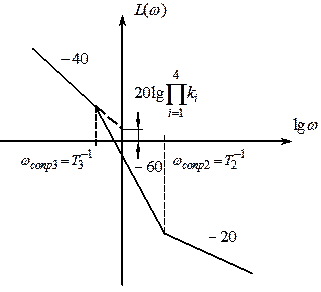
Если в линейной САУ             , то асимптотическая ЛАЧХ системы в разомкнутом состоянии примет следующий вид. 

19. Составление уравнений типовых процессов механообработки. Ортогональное точение детали типа «вал» в патроне.

20. Составление уравнений типовых процессов механообработки. Плоское шлифование деталей.