Частотные критерии устойчивости. Критерий устойчивости Найдквиста. Правило переходов Я. Ципкина. Частотные критерии устойчивости. Критерий устойчивости Найдквиста для ЛАХ

27. Частотные критерии устойчивости. Критерий устойчивости Найдквиста. Правило переходов Я. Ципкина.

Критерий Г. Найквиста позволяет судить об устойчивости САР в замкнутом состоянии по частотным характеристикам системы в разомкнутом состоянии.

Рассмотрим упрощенную структурную схему линейной системы в замкнутом состоянии, реализующей принцип управления по отклонению (используются следующие обозначения: v – задающее воздействие; y – выходная переменная; W_pаз – передаточная функция САР в разомкнутом состоянии).

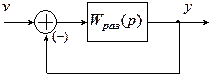
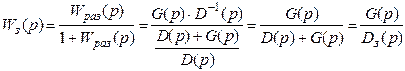
G( p) - входной линейный оператор порядка m ; D(p) – собственный линейный оператор порядка п, являющийся характеристическим полиномом САР в разомкнутом состоянии, причем          .

Передаточная функция САР в замкнутом состоянии:

 

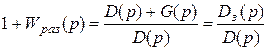где                                   – характеристический полином САР в замкнутом состоянии порядка  п.

Введем вспомогательную функцию вида:

Числитель характеризует устойчивость замкнутой системы, а знаменатель САР в разомкнутом состоянии. 

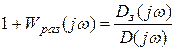Для перехода к частотным характеристикам осуществим замену оператора р дифференцирования  на оператор Фурье jw:

В соответствии с принципом аргумента, линейная САР в разомкнутом состоянии будет устойчивой, если при варьировании частоты входного гармонического сигнала в диапазоне

                 изменение аргумента D(jw) будет составлять                           , а при наличии в

 

характеристическом полиноме k «правых» корней:

Для устойчивости САР в замкнутом состоянии, которое соответствует равенству

 

суммарный угол поворота вектора                           -                                                                   ,

 

•    при устойчивой САР в разомкнутом состоянии равен:                                   ;

 

•     при устойчивой САР в замкнутом состоянии равен:                                   .

На основании последних формул можно сформулировать два определения частотного критерия устойчивости Г. Найквиста:

– если линейная непрерывная САУ в разомкнутом состоянии устойчива, то для ее устойчивости в замкнутом состоянии необходимо и достаточно, чтобы при изменении частоты от 0 до      суммарный поворот вектора                         был равен нулю;

– если линейная непрерывная САУ в разомкнутом состоянии неустойчива, то для ее устойчивости в замкнутом состоянии необходимо и достаточно, чтобы при изменении частоты от 0 до      суммарный поворот вектора  был равен kπ.

В практических расчетах используется другое определение критерия Г. Найквиста:

 Для устойчивости замкнутой линейной непрерывной САУ при устойчивости системы в разомкнутом состоянии необходимо и достаточно, чтобы при изменении частоты от 0 до     АФЧХ системы в разомкнутом состоянии                  не охватывала критическую точку

(-1; .+ j 0).

Рассмотрим графическую интерпретацию данной формулировки критерия Г. Найдквиста.

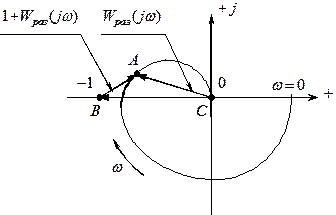
На комплексной плоскости видно, что вектор ВА, соответствующий                      , находится как                                                                         

                                                                     .

В пределе при                вспомогательный вектор

                      будет иметь нулевой фазовый сдвиг

только тогда когда АФЧХ линейной непрерывной

системы в разомкнутом состоянии проходит правее

точки –1.

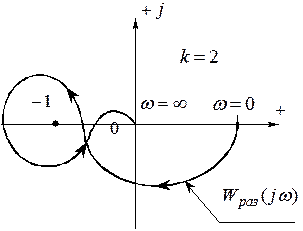
Под охватом понимается полный оборот 

на угол 360⁰.

АФЧХ системы в разомкнутом состоянии с  k = 2

«правыми» корнями, соответствующая случаю

устойчивости замкнутой САР.

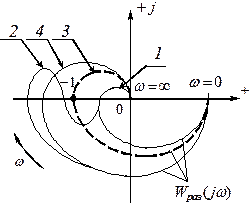
АФЧХ линейной системы в разомкнутом состоянии,

соответствующие устойчивой (1,2), неустойчивой (4) 

и границе устойчивости (3) САР в замкнутом состоянии.

При достаточно сложной форме АФЧХ можно воспользоваться правилом «переходов», предложенным Я. Цыпкиным.

Если при возрастании частоты                  проходит через отрицательную вещественную полуось снизу вверх левее точки (), то такой переход называется положительным, в противном случае отрицательным.

Если характеристика                 начинается (ω = 0) или оканчивается () на участке 

то считается, что АФЧХ системы в разомкнутом состоянии совершает полперехода.

На основании вышеприведенных определений частотный критерий Г. Найквиста формулируется следующим образом: для устойчивости линейной непрерывной САУ в замкнутом состоянии при неустойчивости в разомкнутом состоянии необходимо и достаточно, чтобы разность между положительными и отрицательными переходами

при изменении частоты от 0 до     составляла k/2 раз, где k  – число «правых» корней.

Наибольшее применение на практике правило переходов нашло для ЛЧХ разомкнутой САР.