Другие предметы \ Теория автоматического управления

Частотные критерии устойчивости. Критерий устойчивости Найдквиста. Правило переходов Я. Ципкина. Частотные критерии устойчивости. Критерий устойчивости Найдквиста для ЛАХ, страница 2

Чтобы прийти к формулировке правила для ЛЧХ, следует заметить, что переходам АФХ соответствуют следующие значения и свойства ЛАЧХ – L(ω) и ЛФЧХ - j(ω):

1. L(ω) > 0, т.к.   | W( jω) | > 1;

2.

3. j(w) возрастает при положительном переходе и убывает при отрицательном.

28. Частотные критерии устойчивости. Критерий устойчивости Найдквиста для ЛАХ.

Правило переходов для ЛЧХ

Замкнутая САР устойчива, если в области частот, где L(ω) > 0, разность между числом переходов j(ω) через линии                                  в направлении увеличения фазы  (т.е. снизу вверх) и в направлении уменьшения фазы (т.е. сверху вниз) при возрастании частоты ω равна k/2, где k – количество правых корней характеристического уравнения разомкнутой САР.

При любом формулировке правила переходов в общем случае разность между числом положительных и отрицательных переходов составляет 0,5(k -m), что позволяет определить при неустойчивой замкнутой САР число правых корней k в ее характеристическом уравнении.

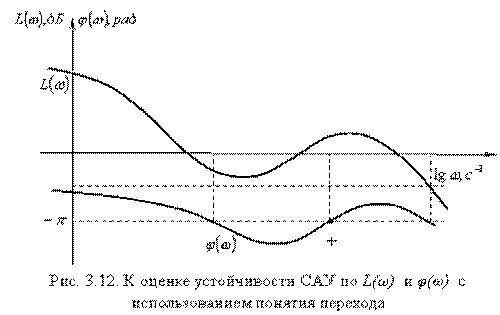imageПравило переходов для ЛЧХ.

В качестве примера приведены

логарифмические амлитудно- и

фазо-частотные характеристики

неустойчивой разомкнутой системы,

имеющей два правых корня k = 2.

При замыкании такая система

становится устойчивой, так как

k+= 1, аk- = 0, и правило

переходов выполняется.

Если линейная система в разомкнутом состоянии является нейтрально устойчивой, т.е. ее характеристический полином с «левыми» корнями содержит один или несколько нулевых

                                                                                                   ,

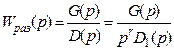где r – порядок астатизма (количество нулевых корней), то АФЧХ претерпевает разрыв при

 и является неопределенной, т.е. неясно, охватывает ли                    критическую точку (–1; j0).

В соответствии с принципом аргумента, элементарный вектор                   для случая  

будет двигаться по мнимой оси из начала координат в       .

Для того, чтобы все корни оставались в левой полуплоскости двумерного комплексного пространства, необходимо обойти справа начало координат по окружности малого радиуса, т.е. принять допущении, что          или               , где            – радиус окружности обхода;

                     – фаза вектора р в малой окрестности начала координат.

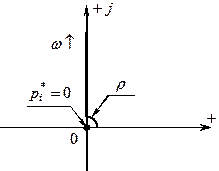
При данном подходе элементарный вектор при изменении частоты от 0 до    поворачивается на угол        

        , что соответствует «левому» корню.

Пространственное расположение вектора

при нулевом корне

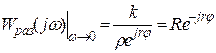
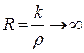
Применительно к АФЧХ в разомкнутом состоянии при             можно записать

где k  – коэффициент передачи, равный отношению свободных членов полиномов числителя и знаменателя             .

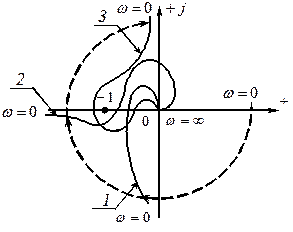
Таким образом, при обходе справа нулевого корня и изменении частоты от 0 до     , вектор  поворачивается по часовой стрелке на угол             и проходит по дуге бесконечно большого радиуса R.

Частотные характеристики линейных САР

с первым (кривая 1), вторым (кривая 2) и

 третьим (кривая 3) порядками астатизма

соответственно в случае устойчивости

системы в замкнутом состоянии.

Аналогичный подход к анализу устойчивости на основании критерия Г. Найквиста можно применить к линейной САР, находящейся на границе устойчивости (пара чисто мнимых корней

           при остальных «левых»).

В этом случае модуль вектора                  в разомкнутом состоянии при ω = β  стремиться к  ∞ , т.е. имеет место неопределенность.

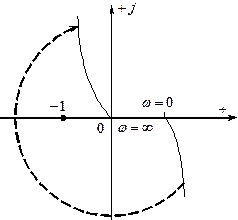
Для ее исключения на данной частоте дугой бесконечно большого радиуса АФЧХ перемещается по часовой стрелке на угол       .

АФЧХ нейтрально устойчивой системы с разомкнутой цепью

воздействий при неустойчивости в замкнутом состоянии.

Таким образом, если линейная непрерывная САУ в разомкнутом состоянии находится на границе устойчивости или нейтрально устойчива, то для ее устойчивости в замкнутом состоянии необходимо и достаточно, чтобы при изменении частоты от 0 до       АФЧХ системы в разомкнутом состоянии не охватывала критическую точку (           )

В практических расчетах также используют критерий Г. Найквиста в логарифмическом масштабе по продольной оси частот. Как было установлено выше, для устойчивости замкнутой САР необходимо и достаточно, чтобы АФЧХ устойчивой системы в разомкнутом состоянии не охватывала точку(            ), т.е. при фазовом сдвиге                  должны соблюдаться неравенства

 


На основании вышеизложенного можно заключить, что для устойчивости замкнутой линейной непрерывной САР при отсутствии «правых» корней в разомкнутом состоянии необходимо и достаточно, чтобы на частоте среза ωc(A(ωc) = 1) выполнялось условие              , или при фазовом сдвиге                   соблюдалось неравенство                или              .

                      

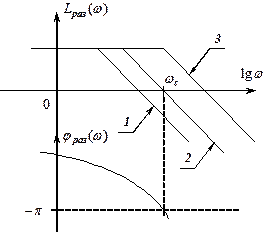
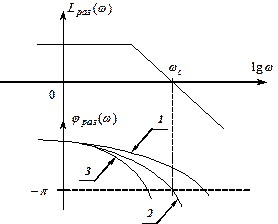
ЛАЧХ и ЛФЧХ устойчивой «1», неустойчивой «3» и находящейся на границе устойчивости «2» САР в замкнутом состоянии. 

Скачать файл