Структурный анализ рычажного механизма. Кинематический анализ рычажного механизма

Определение аналогов ускорений исследуемого механизма графическим методом

Задачу решаем путем построения  плана ускорений, считая w₁ постоянной величенной

1.  Находим ускорение точки А. Точка А принадлежит трем звеньям одновременно. Отсюда:

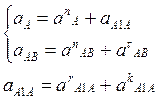
где переносное ускорение ^ кориолисовому ускорению. Строим из полюса. От конца этого вектора откладываем его направление определяется поворотом на 90 градусов скорости камня по направлению угловой скорости звена 3. Затем перпендикулярно этому вектору проводим линию  обозначающею переносное ускорение.

Из полюса проводим    направленный к центру вращения. Из конца этого вектора перпендикулярно ему откладываем линию обозначающую тангенсальное ускорение. Там где эта линия пересечется с линий переносного ускарения ставим точку A. Вектор OA отложенный из центра и будет полное ускорение точки А.

2.  Ускорение точки С строим используя теорему подобия  Вектор BC откладываем на продолжении вектора ОА

3.  Точка D принадлежит двум звеньям причем 5 звено двигается только в вертикальном направлении. Стоим из точки С вектор направленный к оси вращения. Затем перпендикулярно ему рисуем линию до пересечения с вертикалью выходящей из полюса. Точка пересечения точка D.

4.  Ускорения центров масс строим подобно скоростям центров масс.

5.  Измерив нужное вычисляем аналоги ускорениц результаты записываем в таблицы

2.4 Кинематическое исследование машин и механизмов аналитическим методом

Будем находить кинематические характеристики методом Зиновьева (метод замкнутых векторных контуров).

Структурную схему механизма располагаем в прямоугольной системе координат, начало которой помещаем в точку O

Записываем уравнение замкнутости первого контура OAB в векторном виде.

Рассмотрим треугольник ОАВ  и, составив уравнение, спроецируем его на оси координат:

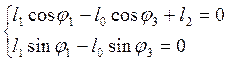                                                                            (2.2)

Здесь переменными являются величины j₃ и l₀

Решив эти два уравнения с помощью программы Mad Cad получим:

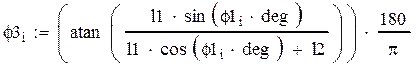
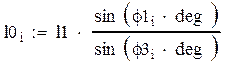
Аналогично рассмотрим многоугольник ВСДМ.

                                                                                                                (2.3)

ОХ:                                                                                     (2.4)

ОY:

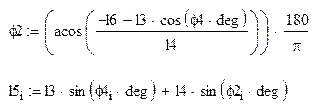
Для нахождения положений точек S₃ S₄ S₅ записываем уравнение замкнутости контура  OАAS3 BCS₄G BCS₅F:

                                                                                                    (2.5)

                                                                                                      (2.6)

        `                                                                                             (2.7)

Из уравнении (2.5) (2.6) (2.7) находим координаты центров масс звеньев :

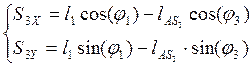                                                                             (2.8)

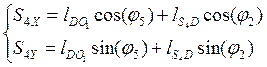                                                                          (2.9)

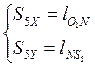                                                                                                                     (2.10)

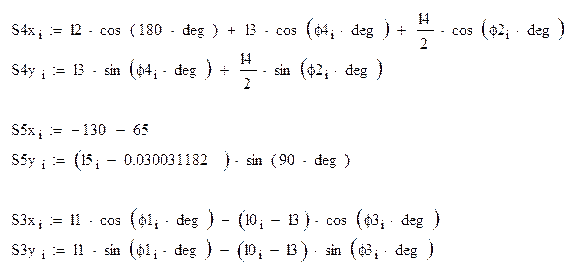
Результаты расчета положений звеньев

Положение	м	м			м
0	236.42	0.11	-32.579	83.083	0.138
1	267.42	0.145	-28.867	81.169	0.132
2	297.42	0.174	-20.957	77.782	0.12
3	327.42	0.193	-11.28	75.021	0.105
4	357.42	0.2	-0.903	73.88	0.088
5	27.42	0.195	9.524	74.693	0.072
6	57.42	0.178	19.379	77.225	0.058
7	87.42	0.15	27.708	80.613	0.047
8	117.42	0.116	32.439	83.007	0.041
9	147.42	0.08	27.958	80.713	0.047
10	177.42	0.06	3.003	73.954	0.082
11	207.42	0.075	-25.408	79.569	0.127

Положение	м	м			м
0	-0.054	-0.048	-0.2	0.093	0.108
1	-0.051	-0.043	-0.202	0.088	0.102
2	-0.046	-0.032	-0.205	0.076	0.09
3	-0.042	-0.018	-0.207	0.061	0.075
4	-0.04	-1.418*10-3	-0.207	0.045	0.058
5	-0.041	0.015	-0.207	0.029	0.042
6	-0.045	0.03	-0.205	0.014	0.028
7	-0.05	0.042	-0.202	2.551*10-3	0.017
8	-0.054	0.048	-0.2	-3.61*10-3	0.011
9	-0.051	0.042	-0.202	2.218*10-3	0.017
10	-0.04	4.714*10-3	-0.207	0.039	0.052
11	-0.049	-0.039	-0.203	0.083	0.097

Кинематические свойства механизма, когда закон движения начального звена еще не известен, находят с помощью кинематических характеристик, называемых аналогами скоростей и ускорений, которые не зависят от времени, а являются функциями обобщенной координаты.

Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w₁=1 рад/с.

Аналитическое определение аналогов скоростей основано на дифференцировании по обобщенной координате уравнений. После дифференцирования уравнений получим

                                                                (2.11)

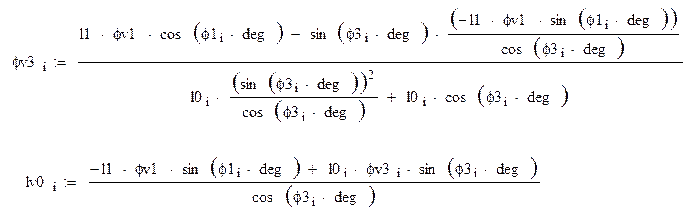
где   абсолютная скорость камня (звено 2)

                                                                     2.12

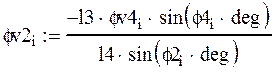
Аналоги скоростей центров масс звеньев 2,3 и 4 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения (2.8) (2.9) и  (2.10).

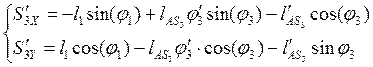                                                    (2.13)   

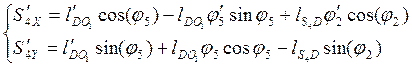                                               (2.14)

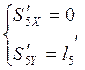                                                                                      (2.15)                                                                                                                 

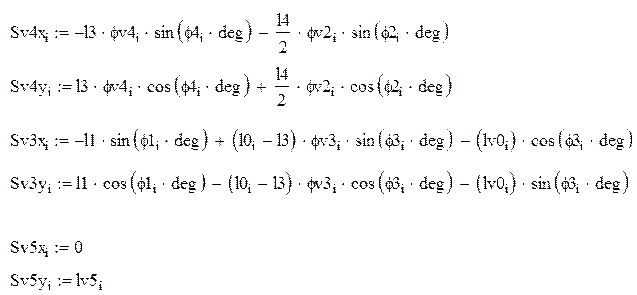
Результаты расчета аналогов скоростей

	j’3	l’0, м	j’2	l’5
0	1.148*10-5	0.07	6.229*10-6	9.384*10-7
1	0.214	0.063	-0.105	-0.018
2	0.301	0.046	-0.11	-0.027
3	0.338	0.025	-0.069	-0.031
4	0.35	2.049*10-3	-5.74*10-3	-0.032
5	0.342	-0.022	0.059	-0.029
6	0.31	-0.043	0.106	-0.024
7	0.235	-0.06	0.111	-0.017
8	0.053	-0.07	0.029	-3.702*10-3
9	-0.428	-0.061	-0.203	0.031
10	-1.158	-6.81*10-3	-0.0603	0.103
11	-0.563	0.056	0.246	0.05

-5.565*10-7	-8.709*10-7	9.383*10-7	2.782*10-7	9.046*10-7
9.299*10-3	0.017	-0.018	-4.65*10-3	-0.018
9.696*10-3	0.025	-0.027	-4.848*10-3	-0.026
5.958*10-3	0.03	-0.031	-2.979*10-3	-0.031
4.963*10-4	0.031	-0.032	-2.481*10-4	-0.032
-5.092*10-3	0.03	-0.029	2.546*10-3	-0.03
-9.261*10-3	0.026	-0.024	4.631*10-3	-0.025
-9.823*10-3	0.019	-0.017	4.912*10-3	-0.018
-2.552*10-3	4.015*10-3	-3.702*10-3	1.276*10-3	-3.659*10-3
0.018	-0.034	0.031	-9.034*10-3	0.033
5.46*10-3	-0.104	0.103	-2.73*10-3	0.103
-0.022	-0.046	0.05	0.011	0.048

Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений (2.11), (2.12).

После дифференцирования уравнений (2.11) получим

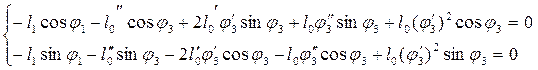                (2.16)

После дифференцирования уравнений (2.12) получим

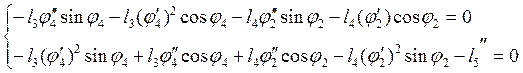                        (2.16)

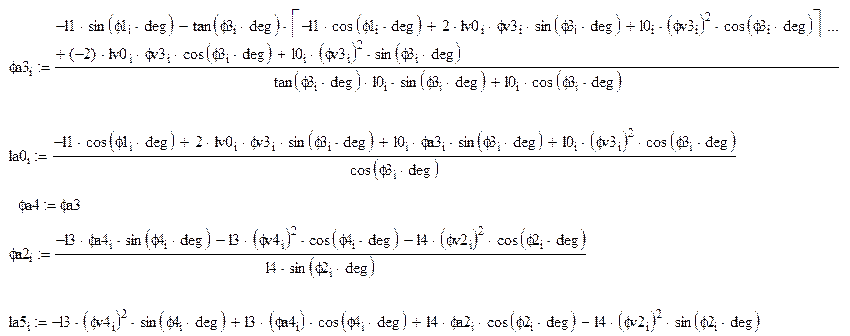
Аналоги ускорений центров масс звеньев 2,3 и 4 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения (2.13), (2.14),  (2.15). Учитываем что и

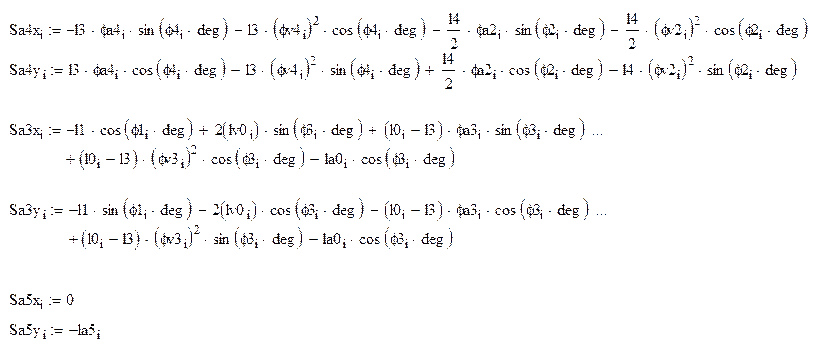
Положение	j’’3	l’’0	j’’2	l’’5
0	0.639	1.258*10-6	-0.347	-0.052
1	0.248	-0.024	-0.082	-0.024
2	0.106	-0.037	0.045	-0.012
3	0.043	-0,043	0.106	-3.713*10-3
4	3.075*10-3	-0.045	0.127	2.73*10-3
5	-0.035	-0.044	0.113	7.216*10-3
6	-0.092	-0.038	0.059	0.011
7	-0.213	-0.027	-0.053	0.017
8	-0.538	-5.8*10-3	-0.289	0.038
9	-1.407	0.049	-0.511	0.109
10	-0.375	0.15	1.372	0.074
11	1.578	0.066	-0.409	-0.154

	S”3x	S”3y	S”4x	S”4y	S”5y
0	-0.044	-0.07	-0.015	-0.05	0.052
1	-0.04	-0.032	-3.579*10-3	-0.023	0.024
2	-0.027	-1.595*10-3	2.1*10-3	-0.013	0.012
3	-0.016	0.024	4.679*10-3	-4.951*10-3	3.713*10-3
4	-0.011	0.044	5.507*10-3	1.138*10-3	-2.73*10-3
5	-0.015	0.059	4.928*10-3	5.878*10-3	-7.216*10-3
6	-0.025	0.069	2.707*10-3	0.01	-0.011
7	-0.038	0.074	-2.266*10-3	0.018	-0.017
8	-0.045	0.072	-0.013	0.039	-0.038
9	-0.037	0.014	-0.022	0.112	-0.109
10	-0.12	-0.153	0.059	0.057	-0.074
11	-0.04	-0.105	-0.018	-0.149	0.153

3. Динамический анализ машины

3.1 Определение параметров динамической модели

Для построения динамической модели исследуемого механизма в качестве звена приведения выбираем начальное звено 1, к которому приводим все силы (моменты), действующие на механизм и моменты инерции подвижных звеньев.

3.1.1 Приведенный момент инерции и его производная

Приведенный момент инерции определяется по  формуле, которая имеет следующий вид:

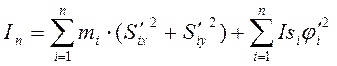                                                                  (3.1)

где n-число подвижных звеньев, массы и моменты инерции которых заданны

Для рассматриваемого зубодолбежного механизма формула 3.1 принимает вид:

(3.2)    

где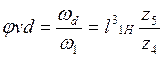 аналог угловой скорости ротора двигателя.

Дифференцируя по общей координате выражение (3.2), находим производную приведенного момента инерции

                                                                                                                                                        (3.3)    

Подставив в (3.2) и (3.3) конкретные данные для механизма с помощью программы Mathcad найдем для 12 положений значеня  момента инерции и его производной (см приложения