Структурный анализ механизма качающегося конвейера

самыми простыми для трехподвижного пространства, в котором существует исследуемый механизм, и, значит, они не могут иметь в своем составе другие более простые группы Ассура.

          2.18. Проводим классификацию структурных групп по И.И. Артоболевскому (табл.1.4).

Классификация структурных групп

Таблица 1.4

№ п/п	Структурная схема	Номер звеньев, образующих группу	Класс,  порядок,  вид
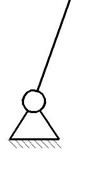
1	O1   1	0-1	Механизм I класса
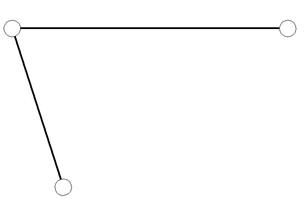
2	3   2   O2   B   A	2-3	II класс 2 порядок 1-вид
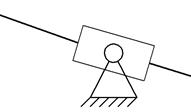
3	5   D,E   C   4	4-5	II класс 2-порядок 3-вид

          2.19. Определяем класс сложного механизма. Механизм относится ко II классу.

2. Кинематический анализ рычажного механизма

2.1.  Определение крайних положений механизма аналитическим методом

2.1.1.  Начальное положение.

Это положениереализуется, когда звенья О1А и АВ выстраиваются в одну линию, причем О1В = АВ–О1А.

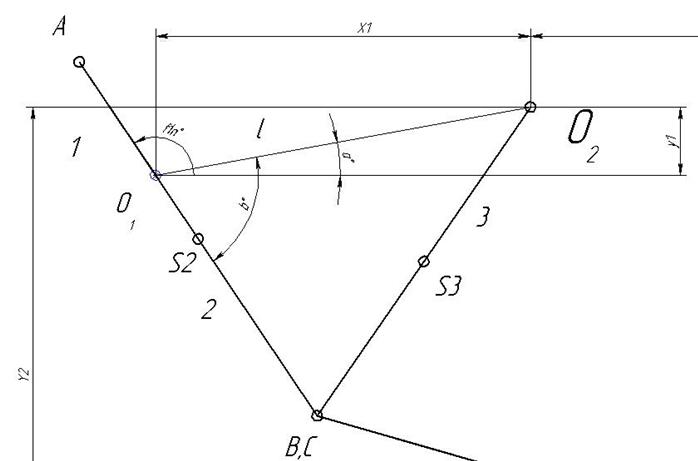
j_н =p-b+a,

где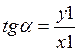

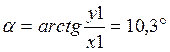
Ð β найдем из ΔО1ВО2

Из условия следует, что м

По теореме косинусов: из ΔО1ВО2 следует, что ,

где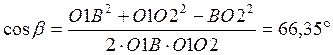       

Тогда j_н = p-b+a = 124°

 

2.1.2.  Конечное положение

Это положение реализуется, когда звенья О1А и АВ выстраиваются в одну линию, причем О1В = АВ + О1А.

j_к = 360°+a-b‘, где найдено в п. 2.1.1

b‘ – найдем из ΔО1BО2

O1О2 = 0,615 (см. п. 2.1.1)

По теореме косинусов ,

где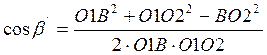  

j_к = 360+a-b‘ =328,8⁰

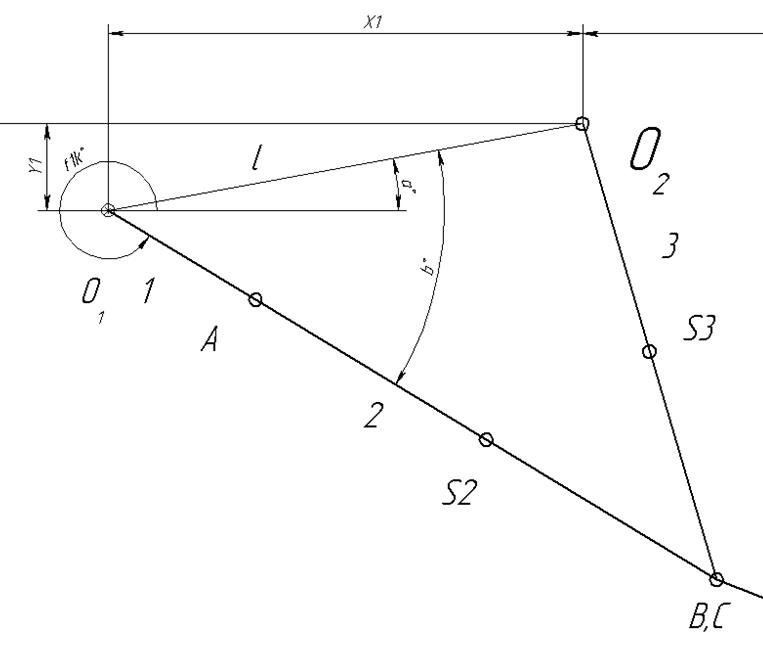
2.2.  Определение положений звеньев механизма.

Положения звеньев механизма можно найти с помощью графического или аналитического метода.

2.2.1.  Графическое построение планов положения исследуемого механизма.

Выбираем масштабный коэффициент длин  m = 0,22/64=0,0034375 м/мм и рассчитываем чертежные размеры звеньев (табл. 2.1).

Таблица 2.1

Планы механизма на чертеже строим следующим образом:

-  Отмечаем на чертеже неподвижные точки О1, O2 и, рисуем в них вращательные кинематические пары.

-  Проводим траектории движения: точки А – окружность радиусом О1А из т. О1; точки В – дугу радиусом О2В из т. О2;.

-  Отмечаем крайние положения механизма:

1. Из точки О1 на дуге О2В радиусом R = AB-О1А = 136 мм. Отмечаем начальное положение – точку В_о
2. Из точки О1 на дуге О2В радиусом R = АВ + О1А = 264 мм. Отмечаем конечное положение – точку В₈. Одновременно на траектории движения точки А (окружности О1А) получаем точки А₀ и А₈ .
3. Начиная от точки А₀ – начало рабочего хода, окружность радиуса О1А делим на 12 частей.
4. Точки деления обозначаем А₁ А₂ А₃ ….в направлении вращения звена О1А.
5. Строим положения кривошипа, соединяя точки Вi с Аi
6. Методом засечек строим план положений механизма для каждого положения кривошипа
7. При построении планов механизма отмечаем положения центров масс звеньев 2 и 3 и строим их траектории.
8. Определяем ход звена 5 Н_max=188.4мм, Н_min=38,6мм, Н= Н_max – Н_min= 149,8мм.

Отсчитывая от начального положения звена 5, откладываем точку на h=0,4Н=59,9мм – соответствующую закону изменения силы Fc. С помощью обратного построения определяем дополнительное положение механизма.

9. Проверяем с помощью линейки и транспортира углы наклона (в положении 4), результаты измерения заносим в таблицу 2.2.

Результаты расчета положений звеньев.

Таблица 2.2

Величина Метод	j10	j20	j30	j40	l4.м	S2x .м	S2y. м	S3x. м	S3y м
Аналитический	213,96	330,24	251,63	165,79	1.022	0.116	-0.294	-0.095	-0.287
Графический	214	330	252	166	1.02	0.115	-0.294	-0.095	-0.287
Отклонение	0,02	0,07	0,15	0,14	0.27	0.86	0	0	0

Погрешность не превышает инженерной (5%), следовательно, расчеты можно считать верными.

2.2.2.  Определение положений аналитическим методом.

Определяем методом векторных замкнутых контуров. В качестве расчетного положения выбираем положение 4.Рисуем схему в расчетном положениии составляем векторные контуры для расчета.

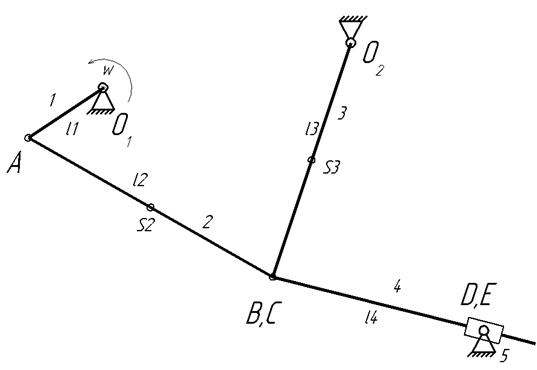
Рисунок 2.3 Схема механизма в расчетном положении

Первый векторный контур:

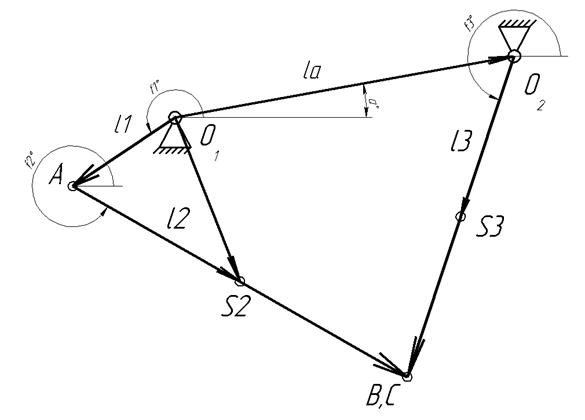
Рисунок 2.4 – Первый векторный контур

Проецируем на оси координат:

                       (2.1)

Проведем замену:

Тогда система примет вид:

                         (2.2)

                  

                   

                  

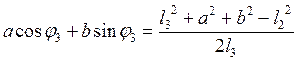
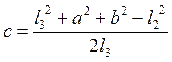
Для решения тригонометрического уравнения произведем замену:

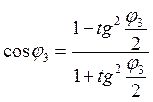    и 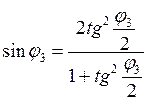                      примем 

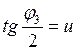
тогда             

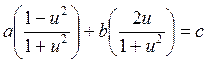
         или   

                   

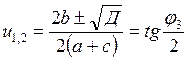
Выбираем Ðj₃ , лежащий во 3-ой четверти:

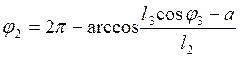
Рассчитываем значения j₂ и j₃ в расчетном положении, решая систему при

а = -0,787; в = -0,233; с =0,469; Д = 1,817;u = -1,386 получим:

;

Значения φ₁ , φ₂ , φ₃ заносим в таблицу 2.2

Второй векторный контур:

В проекциях на оси координат:

 

                         (2.3)

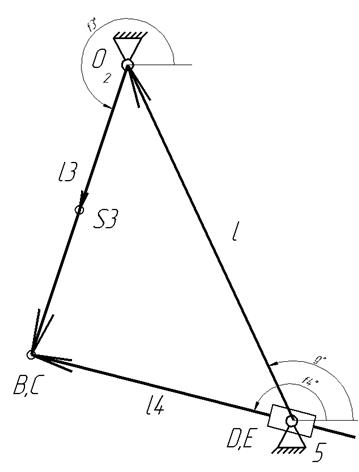
Рисунок 2.5 второй векторный контур

g=π-arctan(Y2/X2)=134°                             l=1,149м

Заметим, что в системе (3) два неизвестных: l₄ и φ₄.

Систему решаем методом вычитания угла из аргументов всех тригонометрических функций.

l4×sin(j4)=l3×sin(j3)+l×sin(g)

l4×cos(j4)=l3×cos(j3)+l×cos(g)

Делим первое уравнение на второе почленно

tg(j4)= l3×sin(j3)+l×sin(g) / l3×cos(j3)+l×cos(g) или :

j4=p+arctg(l3×sin(j3)+l×sin(g) / l3×cos(j3)+l×cos(g))

l4=(l3×sin(j3)+l×sin(g)) / sin(j4)

В расчетном положении:

l₄ = 1.022м            φ₄ = 165.79°

Заносим значения l₄, и φ₄ в таблицу 2.2.

Система уравнений для определения координат центра тяжести звена3:

S3x = 0.5×l3×cos(j3)

S3y = 0.5×l3×sin(j3)                                     (2.4)

Векторный контур для определения координат центра тяжести звена2 (рисунок 2.4):

l1 + 0.5×l2-O1S2 = 0

В проекциях на оси координат:

l1×cos(j1) + 0,5×l2×cos(j2) - S2x = 0

l1×sin(j1) + 0.5×l2×sin(j2) – S2y =0

S2x = l1×cos(j1)+0.5×l2×cos(j2)

S2y = l1×sin(j1)+0.5×l2×sin(j2)          (2.5)

Dрасчетном положении:

S2x = 0.116м                 S2y = -0.294м                S3x = -0.095м                S3y = -0.287м

Заносим значения в таблицу 2.2.

В остальных положениях координаты и углы рассчитаны в MathCAD и результаты расчетов сведены в таблицу 2.3.

Результаты расчёта положений звеньев

Табл. 2.3.

пол	f1°	f2°	f3°	f4°	l4, м	s2x, м	s2y, м	s3х, м	s3y, м
0	123.96	303.96	235.36	164	1.19	0.069	-0.103	-0.172	-0.249
1	153.96	313.83	237.34	164.31	1.17	0.04	-0.151	-0.163	-0.255
2	182	322.47	242.47	165.01	1.118	0.053	-0.217	-0.14	-0.268
3	183.96	323.02	242.93	165.06	1.113	0.055	-0.222	-0.138	-0.269
4	213.96	330.24	251.63	165.76	1.022	0.116	-0.294	-0.095	-0.287
5	243.96	334.85	262.47	165.59	0.908	0.215	-0.344	-0.04	-0.3
6	273.96	336.5	273.85	163.7	0.791	0.33	-0.357	0.02	-0.302
7	303.96	334.45	283.2	160.31	0.703	0.433	-0.331	0.069	-0.295
8	328.79	328.79	286.43	158.66	0.675	0.482	-0.292	0.086	-0.29
9	333.96	327.02	286.26	158.75	0.676	0.486	-0.284	0.085	-0.29
10	3.96	312.77	277.72	162.52	0.753	0.453	-0.237	0.041	-0.3
11	33.96	297.65	260.15	165.74	0.932	0.342	-0.182	-0.052	-0.298
12	63.96	291.92	245.41	165.32	1.087	0.225	-0.121	-0.126	-0.275
13	93.96	295.52	237.62	164.36	1.167	0.133	-0.091	-0.162	-0.255
14	123.96	303.96	235.36	164	1.19	0.069	-0.103	-0.172	-0.249

2.3 Определение скоростей звеньев механизма.

2.3.1.  Аналитическое определение скоростей звеньев механизма.

Аналитическое определение аналдогов скоростей основано на дифференцировании по общей координате (j₁) уравнений (2.1), (2.3), (2.4), (2.5).

После дифференцирования уравнений системы (2.1) получаем:

-l1×j1¢×sin(j1) – l2×f2¢×sin(j2) + l3×f3¢×sin(j3) = 0

l1×j1¢×cos(j1) + l2×f2¢×cos(j2) - l3×f3¢×cos(j3) = 0                                (2,6)

Где j1¢ – аналог угловой скорости звена 1 j1¢ = 1, т.к. ω направлена против хода часовой стрелки.

Решая систему относительно неизвестных получим:

j3¢ = (l1×j1¢×(cos(j1) – sin(j1)×ctg(j2))) / (l3×(cos(j3) – sin(j3)×ctg(j2)))

j2¢ = (l3×j3¢×sin(j3) – l1×j1¢×sin(j1)) / (l2×sin(j2))

В расчетном положении:

j3¢ = 0,333,j2¢ = 0,199 заносим эти значения в таблицу 2.4

Дифференцируем уравнение (2.3):

-l3×j3¢×sin(j3) + l4×j4¢×sin(j4)-l4¢×cos(j4)=0

l3×j3¢×cos(j3) - l4×j4¢cos(j4)-l4¢×sin(j4)=0

Откуда получим:

-l3×j3¢×sin(j3-j4) + l4×j4¢×sin(j4-j4)-l4¢×cos(j4-j4)=×= 0

l3×j3¢×cos(j3-j4) - l4×j4¢cos(j4-j4) -l4¢×sin(j4-j4) = 0          (2.7)

l4¢=-l3×j3¢×sin(j3-j4)

j4¢= l3×j3¢×cos(j3-j4)/l4

Врасчетном положении:

l4¢×= -0,201           j4 = 0,014

Дифференцируем систему (2.4):

S3x¢ = -0.5×l3×j3¢×sin(j3)

S3y = 0.5×l3×j3¢×cos(j3)                              (2.8)

Дифференцируем систему (2.5):

S2x¢ = -l1×j1¢×sin(j1) – 0,5×l2×j2¢×sin(j2)

S2y¢ = l1×j1¢×cos(j1) + 0,5×l2×j2¢×cos(j2)                                (2.9)

В расчетном положении:

S2x¢ = 0,157,S2y¢ =-0,123                   S3x¢ = -0,095,S3y¢ =-0,032

заносим в таблицу 2.4

В остальных положениях скорости рассчитаны в MathCAD и результаты расчетов сведены в таблицу 2.5.

Результаты расчета скоростей в положении 1.

Таблица 2.4

Величина Метод	j2¢	j3¢	j4¢	l4¢	S2x¢	S2y¢	S3x¢	S3y¢
Аналитический	0.199	0.333	0.014	-0.201	0,157	-0,123	0,095	-0,032
Графический	0.2	0.332	0.014	0,201	0,156	-0,122	0,0945	-0,031
отклонение	0.5	0.3	0	0	0,64	0,82	0,53	3,12

Погрешность в пределах инженерной. Расчеты считаем верными.

Результаты расчёта аналогов скоростей

Табл. 2.5.

пол	f1°	f2`	f3`	f4`	l4`	s2x`	s2y`	s3x`	s3y`
0	123.96	0.32	0	0	0	-0.091	-0.061	0	0
1	153.96	0.327	0.129	0.019	-0.074	-0.016	-0.12	0.033	-0.021
2	182	0.283	0.235	0.028	-0.139	0.067	-0.143	0.063	-0.033
3	183.96	0.278	0.242	0.028	-0.143	0.073	-0.143	0.065	-0.033
4	213.96	0.199	0.333	0.014	-0.201	0.157	-0.123	0.095	-0.032
5	243.96	0.107	0.381	-0.03	-0.229	0.213	-0.063	0.114	-0.015
6	273.96	-0.001	0.363	-0.096	-0.206	0.219	0.015	0.11	0.007
7	303.96	-0.145	0.237	-0.11	-0.12	0.161	0.078	0.07	0.016
8	328.79	-0.32	0	0	0	0.057	0.094	0	0
9	333.96	-0.362	-0.067	0.037	0.032	0.029	0.093	-0.02	-0.006
10	3.96	-0.556	-0.493	0.168	0.27	-0.156	0.09	-0.148	-0.02
11	33.96	-0.379	-0.594	0.029	0.358	-0.238	0.122	-0.177	0.031
12	63.96	-0.011	-0.372	-0.036	0.222	-0.201	0.095	-0.102	0.047
13	93.96	0.224	-0.158	-0.024	0.091	-0.15	0.018	-0.04	0.026
14	123.96	0.32	0	0	0	-0.091	-0.061	0	0

2.3.2.  Графическое определение скоростей (построение планов скоростей).

Решение этой задачи графическим методом основано на построении плана скоростей для первого положения механизма план строим следующим образом.

1. Находим скорость точки А:

Va = w1×l1 = 0.22×1 = 0.22м/с

2. Из полюса плана скоростей Р – откладываем вектор Ра = 64мм , изображающий скорость точки А. этот вектор _┴ ОА и направлен в сторону вращения звена 1.
3. Подсчитываем масштабный коэффициент скоростей.

m_v = Va / pa = 0.22 / 64 = 0.0034375 (м/с)/мм

4. Для определения скоростей точки В рассмотрим ее двояко:

Точка В в движении звена 2 :

Vb = Va + Vb/a

Про Vb/aизвестно, что оно перпендикулярно АВ

Из точки а, плана скоростей, откладываем направление Vb/a

С другой стороны точка b участвует во вращательном движении звена 3 относительно точки О2.

Vb = Vb/о2

Из полюса плана скоростей – р перпендикулярно О2В, до пересечения с направлением Vb/a строим направление Vb. Точка пересечения построенных направлений (т. b) определит отрезки ab= 40 мм аналог Vb/a = ab×m_v = 1375 м/с, и pb=58.5мм – аналог Vb/c = pb×m_v = 0,201 м/с.

Зная линейные скорости определим угловые:

w3 = Vb/c / l3 = 0.201 / 0,605 = 0.332 c^-1

w2 = Vb/a / l2 = 0.1375 / 0.6875 = 0,2 c^-1

Полученные значения заносим в табл. 2,4

5. Определяем скорость точки Д.

Vd = Vb + Vd/b

Из точки b плана скоростей откладываем направление Vb/d перпендикулярно ВД.

С другой стороны ползун Д движется по направляющей. Из полюса р, параллельно траектории движения Д до пересечения с линией, определяющей направление Vd/b, строим направление Vd. Точка пересечения – точка d.

bd = 4.2мм – аналог Vd/b = bd×m_v = 0,0144 м/с²

w4 = Vd/b / l4 = 0.0144 / 1,02 = 0,014 м/с

pd = 58.4мм – аналог Vd = pd×m_v = 0,201 м/с

Заносим полученные данные в табл 2.4

По теореме подобия найдем координаты скоростей центров масс