Синтез корректирующих устройств САР по ЛЧХ. Построение желаемой ЛАЧХ в низкочастотном диапазоне. Синтез корректирующих устройств САР по ЛЧХ. Построение желаемой ЛАЧХ в средне и высокочастотном диапазонах

49. Синтез корректирующих устройств САР по ЛЧХ. Построение желаемой ЛАЧХ в низкочастотном диапазоне.

Данный метод синтеза является структурно – параметрическим, т.к. позволяет определять структуру и параметры КУ по заданным показателям качества и характеристикам неизменяемой части САР.

Достоинство метода. Возможность упрощения корректирующего устройства по близости частотных характеристик синтезируемой и желаемой САР.

Ограничение применения метода. Следящие системы с единичной главной обратной связью.

Реализация метода включает шесть этапов.

1. Формулировка исходных данных и технических требований к САР.

2. Построение ЛАЧХ L_Н(ω) нескорректированной разомкнутой САР.

3. Построение желаемой ЛАЧХ L_ж(ω) скорректированной САР.

4. Выбор схемы включения КУ и расчет его ЛАЧХ L_КУ(ω).

5. Выбор принципиальной схемы физической реализации КУ по его L_КУ(ω) и расчет параметров данной схемы.

6. Проверочный расчет САР на соответствие заданным техническим требованиям.

Исходные данные о неизменяемой части системы (усилитель, исполнительный механизм и т.п.) задаются передаточной функцией нескорректированной разомкнутой САР W_Н(p).

Технические требования к САР. Требования к точности (установившаяся ошибка при определенных воздействиях на САР) и показатели качества переходного процесса при единичном ступенчатом задающем воздействии.

Будем рассматривать объект управления, поведение которого описывает передаточная функция W₀(p).

Требования к поведению замкнутой системы заданы в виде оценок переходного процесса, в качестве которых используются статическая ошибка δ_ст, перерегулирование (σ%) и быстродействие t_n.

Необходимо определить передаточную функцию W_k(p) корректирующего звена (регулятора), включение которого в систему обеспечит в ней заданное качество работы.

Предполагается, что корректирующее звено (регулятор) находится на входе системы, и расчетная структурная схема системы имеет вид, изображенный ниже.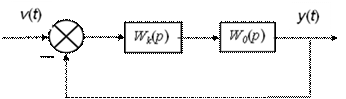

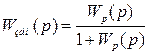Передаточная функция разомкнутой системы:                                                            

Передаточная функция замкнутой системы:

Если удастся сформировать заданную передаточную функцию или частотную характеристику для разомкнутой системы, то тем самым можно обеспечить требуемые свойства в замкнутой системе.

Построение желаемой ЛАЧХ скорректированной системы

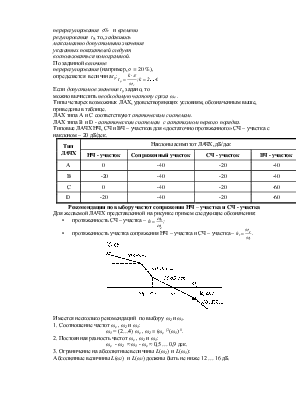
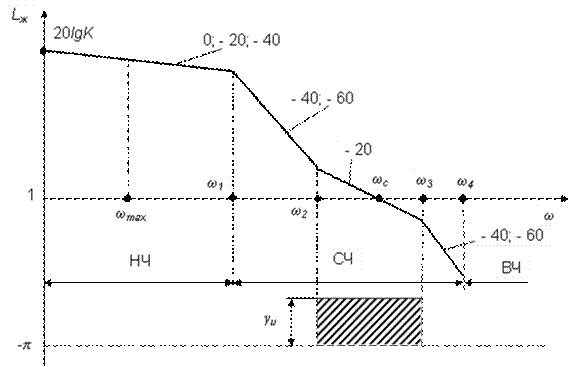
Построение желаемой ЛАЧХ осуществляется раздельно в низкочастотном (НЧ), среднечастотном (СЧ)  и высокочастотном (ВЧ) диапазонах с учетом заданных технических требований к САР.

Построение ЛАЧХ в низкочастотном  диапазоне (НЧ - участок)

На НЧ – участке вид L_ж(ω) определяется в основном требованиями к точности регулирования, а следовательно,  величиной коэффициента усиления системы, порядком ее астатизма, значением коэффициента ошибки и т.д.

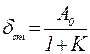1. В систему на вход подается ступенчатый входной сигнал: v(t) = А₀ • 1(t).

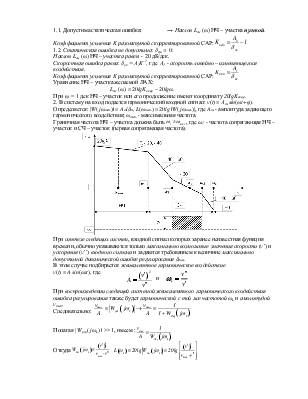
1.1. Допустима статическая ошибка:                  → Наклон L_ж(ω) НЧ – участка нулевой.

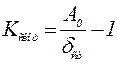Коэффициент усиления K разомкнутой скорректированной САР:

1.2. Статическая ошибка не допустима: δ_ст = 0:

Наклон L_ж(ω) НЧ – участка равен: - 20 дБ/дек.

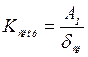Скоростная ошибка равна: δ_ск = А₁K^-1, где  А₁ - скорость линейно – изменяющегося воздействия.

Коэффициент усиления K разомкнутой скорректированной САР: 

Уравнение НЧ – участка желаемой ЛАХ:

                                        L_ж(ω) = 20lgK_скор – 20lgω.

При ω  = 1 дек НЧ – участок или его продолжение имеют координату 20lgK_скор.

2. В систему на вход подается гармонический входной сигнал: v(t) = А_m sin(ωt+φ).

Определяется: |W( jω_max)| = A_m/δ_m, L(ω_max) = 20lg |W( jω_max)|, где A_m - амплитуда задающего гармонического воздействия; ω_max - максимальная частота.

Граничная частота НЧ – участка должна быть               , где ω₁ - частота сопрягающая НЧ – участок и СЧ – участок (первая сопрягающая частота).

При синтезе следящих систем, входной сигнал которых заранее неизвестная функция времени, обычно указываются только максимально возможные  значения скорости (v’) и ускорения (v’’) входного сигнала и задаются требованием к величине максимально допустимой динамической ошибке регулирования δ_дин.

В этом случае подбирается эквивалентное гармоническое воздействие 

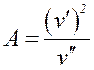
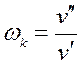v(t) = A sin(ω_kt), где

                                                                        и

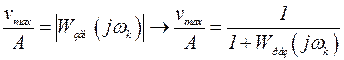При воспроизведении следящей системой эквивалентного гармонического воздействия ошибка регулирования также будет гармонической с той же частотой ω_k и амплитудой v_max.

Следовательно:

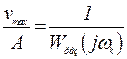Полагая | W_раз( jω_k) | >> 1, имеем :

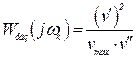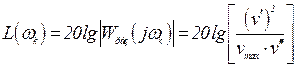Откуда

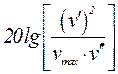Из последнего выражения следует, что эквивалентное входное воздействие будет воспроизводиться следящей системой с ошибкой, не превышающей v_max, если при ω = ω_k ордината желаемой ЛАХ будет не менее  

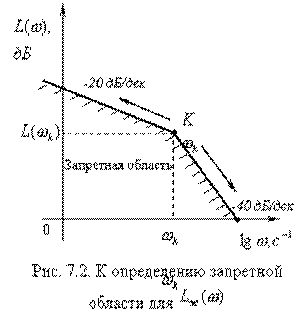Точку К с координатами (ω_k ;L(ω_k )) называют контрольной точкой.

На этом рисунке указаны две прямые, пересекающиеся  в точке К, имеющие наклон

•   - 20 дБ/дек при ω  < ω_k ;

•   - 40 дБ/дек при   ω > ω_k .

 Уравнения этих прямых получены

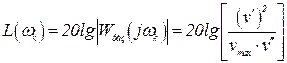 на основании выражения:

при уменьшении  скорости  и ускорения

 входного сигнала по отношению

к их  максимально возможным значениям.

Данные прямые  представляют собой границы

запретной зоны для желаемой ЛАХ

следящей системы с астатизмом первого порядка.