Расчет механизма долбёжного станка

Кинематическая пара F(F’) является разнесённой, и поэтому считаем её как одну кинематическую пару F.

2.3. Классифицируем кинематические пары механизма (табл.2.1).

Классификация кинематических пар

Таблица 2.1

№ п/п	Номер звеньев, образующих пару	Условное обозначение	Название	Подвижность	Высшая /низшая	Замыкание	Открытая/закрытая
1	0-1		Вращательная	1	Н	Г	З
2	1-2		Вращательная	1	Н	Г	З
3	2-3		Поступательная	1	Н	Г	З
4	3-0		Вращательная	1	Н	Г	З
5	3-4		Вращательная	1	Н	Г	З
6	4-5		Вращательная	1	Н	Г	З
7	5-0		Поступательная	1	Н	Г	З

Исследуемый механизм состоит только из одноподвижных кинематических пар ,где число одноподвижных кинематических пар в механизме, - общее число кинематических пар в механизме.

2.4. Классифицируем звенья механизма (табл.2.2).

Классификация звеньев

Таблица 2.2

Механизм имеет четыре  двухвершинных (t=2) линейных звена 1,2,4,5; одно  трехвершинное (t=3) звено 3, которое является базовым (T=3); пять (n=5) подвижных звеньев.

2.5. Находим число присоединений к стойке. Механизм долбёжного станка имеет три (S=3) присоединений к стойке.

2.6. Выделяем в станке простые, элементарные и с разомкнутыми цепями механизмы. В исследуемом сложном механизме можно выделить один элементарный механизм (рис.2.2)

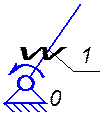
Рис 2.2. Элементарный механизм

и два простых, один из которых является кулисным (рис 2.3),

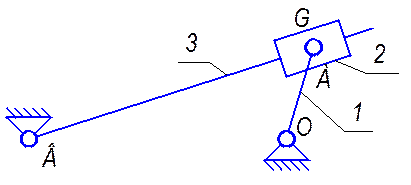
Рис. 2.3. Кулисный механизм

а второй - коромыслово-ползунным (рис. 2.4).

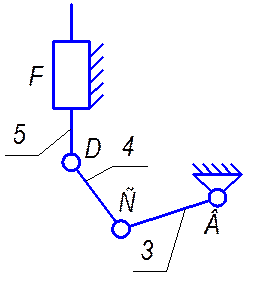
Рис 2.4. Коромыслово-ползунный механизм

Механизмов с разомкнутыми кинематическими цепями в исследуемом станке нет.

          2.7. Выявляем простые стационарные и подвижные механизмы. Механизм долбёжного станка имеет в своем составе только простые стационарные механизмы.

          2.8. Находим звенья закрепления и присоединения. В исследуемом сложном механизме станка звеньев закрепления нет. У него одно звено присоединения- звено 3 (коромысло). Звено 3 одновременно входит в два простых механизма - кулисный и коромыслово-ползунный. Значит для этого звена .

          2.9. Классифицируем механизм станка. Исследуемый механизм имеет постоянную структуру, является сложным и однотипным. Он состоит из одного элементарного механизма и двух стационарных простых, которые имеют в своем составе только замкнутые кинематические цепи.

          2.10. Определяем подвижность простых механизмов. Анализ движений звеньев механизма и элементов кинематических пар показывает, что и исследуемые простые механизмы, и сам сложный механизм существуют  в трехподвижном  пространстве, в котором разрешены следующие простейшие независимые движения: два поступательных x и yвдоль соответствующих осей; одно вращательное  вокруг оси Z. Подвижность элементарных механизмов может быть определена по одной из следующих формул:

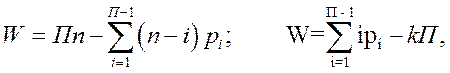(2.1)

Формулы для определения подвижности этих механизмов примут вид соответственно:

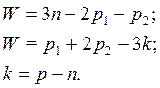 (2.2)

где W – подвижность механизма; n– число подвижных звеньев механизма; i– целочисленный индекс; – число кинематических пар i-той подвижности;– число независимых контуров; 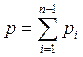 – общее число кинематических пар в механизме.

Определим подвижность кулисного механизма. Этот механизм имеет: три  подвижных звена 1, 2, 3; четыре  одноподвижные кинематические пары A, В, C, G. Тогда его подвижность определиться:

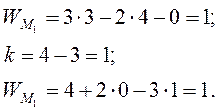
Найдем подвижность коромыслово-ползунного механизма. Механизм имеет: три  подвижных звена 3, 4, 5 и четыре кинематические пары B, C, D, F. Так как этот  механизм по количественному и качественному составу кинематических пар и звеньев ничем не отличается от кулисного, то его подвижность определяется по тем же формулам и также равна единице.

          2.11. Подвижность механизмов с незамкнутыми кинематическими цепями. Так как в механизме станка нет механизмов с незамкнутыми кинематическими цепями, то нет необходимости определять их подвижность.

2.12. Определяем подвижность сложного механизма. Подвижность сложного механизма станка определяется по формуле:

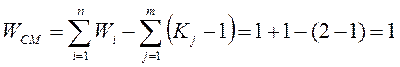 (2.3)

где  j-индекс (порядковый номер) общего звена; m-число звеньев присоедине-

ния в механизме; n-число простых механизмов; i-индекс (порядковый номер) простого механизма.

Так как исследуемый сложный механизм является однотипным, его подвижность также можно определять по формулам 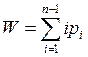.Подставив в эти

формулы исходные данные , найдем подвижность этого сложного механизма:

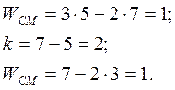
Видно, что полученные результаты совпадают.

2.13. Проводим анализ структурной модели механизма. Проверяем, соответствует ли исследуемый механизм структурной математической модели. Механизм имеет: семь одноподвижных  кинематических  пар; пять  подвижных звеньев, из которых одно  базовое  трехвершинное  и четыре двухвершинных ; три присоединения к стойке  и нет звеньев закрепления .

Математическая структурная модель:

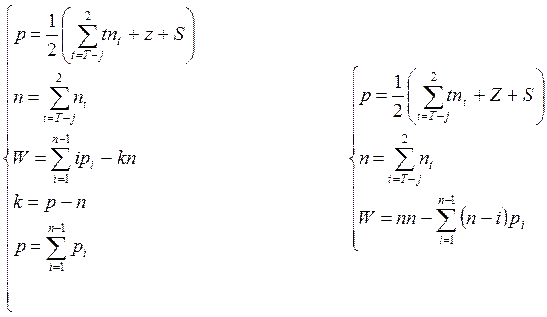 (2.4)

где – число подвижных t-вершинных звеньев; z – число закреплений (число, определяющее количество присоединений нестационарных механизмов к стационарным).

Подставив исходные данные в математическую структурную модель, получим:

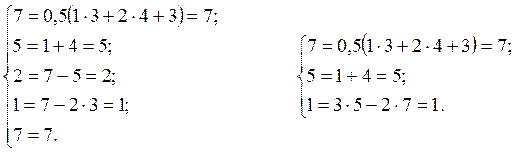
Так как уравнения превратились в тождества, то исследуемое устройство имеет правильную структуру и является механизмом.

2.14. Выделяем в исследуемом устройстве механизм I класса. В соответствии с классификацией И.И. Артоболевского механизм I класса для исследуемого механизма совпадает с элементарным механизмом.

          2.15.

В

Выделяем структурные группы Ассура. В механизме станка можно выделить следующие структурные группы (рис.2.5):

Рис.2.5. Структурные группы Ассура

Видно, что выделенные структурные группы полностью подобны по видовому и количественному составу звеньев и кинематических пар. Каждая из структурных групп имеет: два подвижных звена (п’ = n’₂ = 2), причем все звенья двухвершинные (t = 2) и, значит, базовое звено также имеет две вершины (Т = 2); три (р = 3) одноподвижные (р₁ = 3) кинематические пары, из которых две внешние (S’ = 2).

          2.16. Проверим, соответствуют ли выделенные структурные группы их математическим моделям. Так как группы структурно подобны, то проверку ведем только по одной группе, например