Запасы устойчивости линейных непрерывных САР. Устойчивость линейных непрерывных САР. Области устойчивости. D-разбиение по двум параметрам. Структурная устойчивость линейных непрерывных САР

найти нельзя, не построив всех остальных областей (недостаток метода).

3. Граница D – разбиения отделяет D – области друг от друга. Она (граница) является отображением мнимой оси плоскости корней в пространстве варьируемых параметров. Это означает, что в каждой точке границы D – разбиения соответствует характеристическое уравнение, имеющее один или несколько (обычно 2) корней на мнимой оси.

      Это свойство позволяет находить уравнение границы D – разбиения  из характеристического уравнения после подстановки s = jw (так как отображаются корни на мнимой оси). Характеристическое уравнение при этом должно быть решено относительно варьируемых параметров.

4. Для границы D – разбиения осуществляется штриховка по определенным правилам. Эта штриховка позволяет определить область с наибольшим количеством левых корней в характеристическом уравнении.

       Такая область называется областью – претендентом на область устойчивости.

Переход через границу D – разбиения с заштрихованной стороны на незаштрихованную сопровождается переходом корней характеристического уравнения из левой полуплоскости в правую полуплоскость в количестве, равном кратности штриховки (одинарная или двойная).

Поэтому область – претендент должна быть со всех сторон окружена заштрихованными сторонами границы.

5. Для любой точки области – претендента производится проверка системы на устойчивость по любому известному критерию.

Если результат проверки положительной, то область – претендент является искомой областью устойчивости, в противном случае области устойчивости не существует в плоскости варьируемых параметров.

Рассмотрим характеристическое уравнение третьего порядка:

Соответствующее ему пространство коэффициентов а₁, а₂, а₃ представлено ниже.

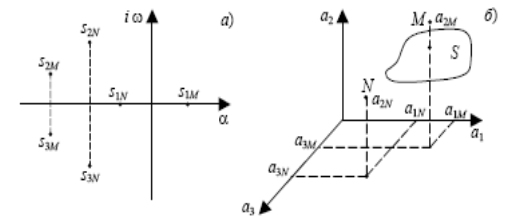
Связь корней характеристического уравнения

 и пространства коэффициентов:

 а – плоскость корней

характеристического уравнения;

 б – пространство параметров

Каждой точке пространства соответствует вполне определенный полином и вполне определенные три корня.

Точка М имеет координаты (а_1М, а_2М, а_3М), и следовательно, характеристический полином записывается в виде: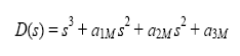

и имеет корни S_1М, S_2М, S_3М.

Когда один из корней равен 0 или +jω, тогда точка пространства будет удовлетворять уравнению:

При –∞ < ω < ∞ этому уравнению соответствует некоторая поверхность Q.

Если корни мнимые, то точка в пространстве коэффициентов попадает на эту поверхность Q.

При пересечении ее корни переходят из одной полуплоскости в другую.

Таким образом, поверхность Q разделяет все пространство на области с равным количеством правых и левых корней, их обозначают D(k), где k– число правых корней характеристического уравнения.

Определение. Разбиение пространства параметров на области с одинаковым числом правых корней внутри каждой области и выделение среди полученных областей области устойчивости называется методом D - разбиения.

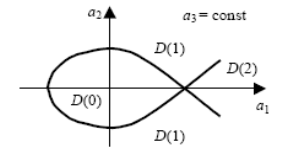Для уравнения третьего порядка можно выделить 4 области D(3), D(2), D(1), D(0), последняя будет областью устойчивости.

Граница D - разбиения в плоскости коэффициентов

для  характеристического уравнения третьей степени

31. Устойчивость линейных непрерывных САР. Области устойчивости. D – разбиение по одному параметру.

Учитывая тот факт, что параметры системы могут принимать только