Приближенные методы решения обыкновенных дифференциальных уравнений: Методические указания к выполнению лабораторной работы № 11

Лабораторная работа № 11

Приближенные методы решения обыкновенных дифференциальных уравнений

Цель работы:           Получить практические навыки решения обыкновенных дифференциальных уравнений методами Эйлера и Рунге-Кутта.

Содержание отчета

1.  Постановка задачи. Исходные данные.

2.  Анализ решения задачи. Алгоритм решения (блок – схема алгоритма).

3.  Текст программы.

4.  Результат выполнения программы.

5.  Выводы по работе.

Постановка задачи

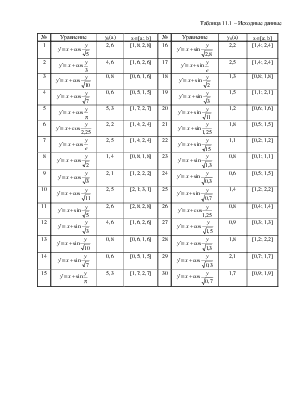
1.  Используя метод Эйлера и метод Рунге-Кутта, составить таблицу приближенных значений интеграла дифференциального уравнения y`=f(x, y), удовлетворяющего начальным условиям y(x₀)=y₀ на отрезке [a; b]; шаг h=0,1. Все вычисления вести с четырьмя десятичными знаками. Исходные данные для расчетов взять из таблицы 11.1.

2.  Вывести полученные данные на экран в следующем виде:

, где    Y1 – решение, полученное методом Эйлера;

Y2 – решение, полученное методом Рунге-Кутта;

E   – погрешность расчета методом Эйлера.

3.  Анализируя полученные значения сделать выводы о точности численного метода расчета методом Эйлера в зависимости от номера шага интегрирования.

Краткие теоретические сведения

Решить дифференциальное уравнение вида y’=f(x,y) численным методом – это значит для заданной последовательности аргументов x₀,x₁,…,x_n и числа y₀, не определяя функцию y=F(x), найти такие значения y₁,y₂,…,y_n, что y_i=F(x_i) (i=1,2,…,n) и F(x₀)=y₀.

Таким образом, численные методы позволяют вместо нахождения функции y=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k-x_k-1 называется шагом интегрирования.

Рассмотрим некоторые из численных методов.

Метод Эйлера

Данный метод является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Пусть дано дифференциальное уравнение первого порядка

                                                                                                                                                 (1)

с начальным условием

.                                                                                                                                                 (2)

Требуется найти решение уравнения (1) на участке [a, b].

Разобьем участок [a, b] на n равных частей и получим последовательность x₀,x₁,…,x_n, где x_i=x_o+ih (i=0,1,2,…,n), а h=(b-a)/n – шаг интегрирования.

Выберем k-й участок [x_k, x_k+1] и проинтегрируем уравнение (1):

,

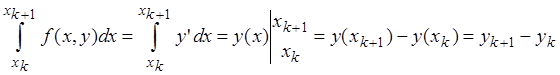т.е.

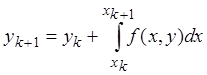.                                                                                                                                                 (3)

Если в последнем участке подынтегральную функцию на участке [x_k, x_k+1] принять постоянной и равной начальному значению в точке x=x_k, то получим

.

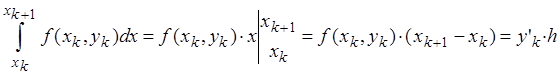Тогда формула (3) примет вид

                                                                                                                                               (3’)

Обозначив , т.е. , получим

.                                                                                                                                                 (4)

Продолжая этот процесс и каждый раз принимая подынтегральную функцию на соответствующем участке постоянной и равной ее значению в начале участка, получим таблицу решений дифференциального уравнения на заданном участке [a, b].

Для оценки погрешности на практике , как правило, используют метод «дойного просчета». Сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом h/2. погрешность более точного значения y^*_n оценивается формулой

.                                                                                                                                                 (5)

Метод Рунге-Кутта

Метод Рунге-Кутта является одним из методов повышенной точности. Он имеет много общего с методом Эйлера.

Пусть на отрезке [a, b] требуется найти численное решение уравнения (1) с начальным условием (2).

Разобьем участок [a, b] на n равных частей точками x_i=x_o+ih (i=0,1,2,…,n), где  

h=(b-a)/n – шаг интегрирования. В методе Рунге-Кутта, так же и в методе Эйлера, последовательные значения y_i искомой функции y определяют по формуле (4).

Если разложить функцию y в ряд Тейлора и ограничиться членами до h⁴ включительно, то приращение функции Δy можно представить в виде:

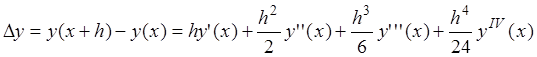,                                                                                                                                                 (6)

где y΄΄(x), y΄΄΄(x), y^IV(x) – определяются последовательным дифференцированием из уравнения (1).

Вместо непосредственных вычислений по формуле (6) в методе Рунге-Кутта определяются четыре числа:

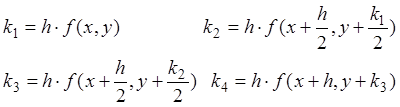                                                                                                                                                 (7)

При этом, значение Δy, вычесленное по формуле (6), с точностью до четвертых степеней будет равно:

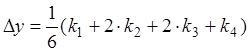                                                                                                                                                 (8)

Таким образом, для каждой пары текущих значений xi, yi по формуле (7) определяются значения:

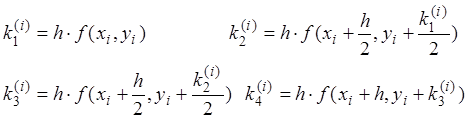                                                                                                                                                 (9)

по формуле (8) находится 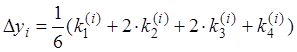, а затем .

Данный метод имеет порядок точности h⁴на всем отрезке [a, b]. Оценка точности метода очень затруднительна. Грубую оценку погрешности можно получить с помощью «двойного просчета» по формуле

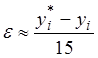,                                                                                                                                                (10)