Лабораторная работа №1
Цель работы: Решить уравнения методами:
а) группировки,
б) замены переменной.
Теоретическая часть работы
Способ группировки разложение на множители
Для того, чтобы разложить многочлен ![]() на множители:
на множители:
1 – Объединим слагаемые попарно в группы (говорят
"сгруппируем слагаемые"): два в одну группу, и два - в другую ![]() .
.
2 – В каждой
паре вынесем за скобки общий множитель![]() .
.
3 – Заметим,
что оба полученных слагаемых также имеют общий множитель, который можно вынести
за скобки ![]() .
.
Не любая группировка приводит к разложению на множители. В случае неудачи попробуйте сгруппировать по-другому, или вообще попытайтесь применить другой метод.
Рассмотрим решение уравнения способом разложения на множители на конкретном примере:
x3-8x2-x+8=0
Применив способ группировки, получим:
x2(x-8) - (x-8) = 0
(x2-1)(x-8) = 0
(x-1)(x-1)(x-8) = 0
Помня, что произведение равно 0 в случае, если один из множителей равен 0, получим корни уравнения:
x1 = 1; x2= -1; x3 =8
Метод введения новой переменной
Пример.
Решить уравнение:
![]() .
.
Введем новую переменную ![]() ,
учитывая, что
,
учитывая, что ![]() , получаем
квадратное уравнение у2 +у – 42=0 , корни которого -7 и 6.
Возвращаясь к переменной х, получаем уравнения
, получаем
квадратное уравнение у2 +у – 42=0 , корни которого -7 и 6.
Возвращаясь к переменной х, получаем уравнения ![]() и
и ![]() , последнее не имеет корней, т.к. арифметический
квадратный корень – неотрицательное число, а первое уравнение можно решить,
используя определение арифметического квадратного корня 62
= х2 +11 , решение которого х=5 и х=-5.
, последнее не имеет корней, т.к. арифметический
квадратный корень – неотрицательное число, а первое уравнение можно решить,
используя определение арифметического квадратного корня 62
= х2 +11 , решение которого х=5 и х=-5.
Ответ: -5; 5.
Если уравнение можно свести к уравнению, содержащему два или несколько одинаковых выражений, то это уравнение можно решить методом замены переменной. Для этого заменяют такое выражение другой переменной, получают новое уравнение относительно новой переменной, решают его, затем осуществляют обратную замену, возвращаясь к прежней переменной.
Структурная схема программы:
а) способ группировки разложение на множители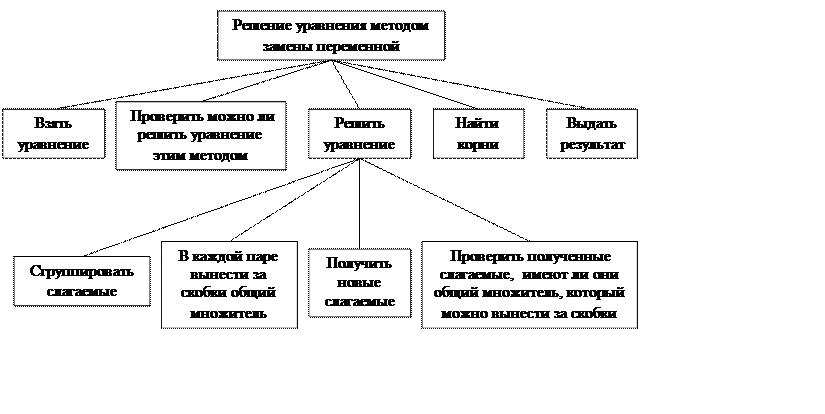
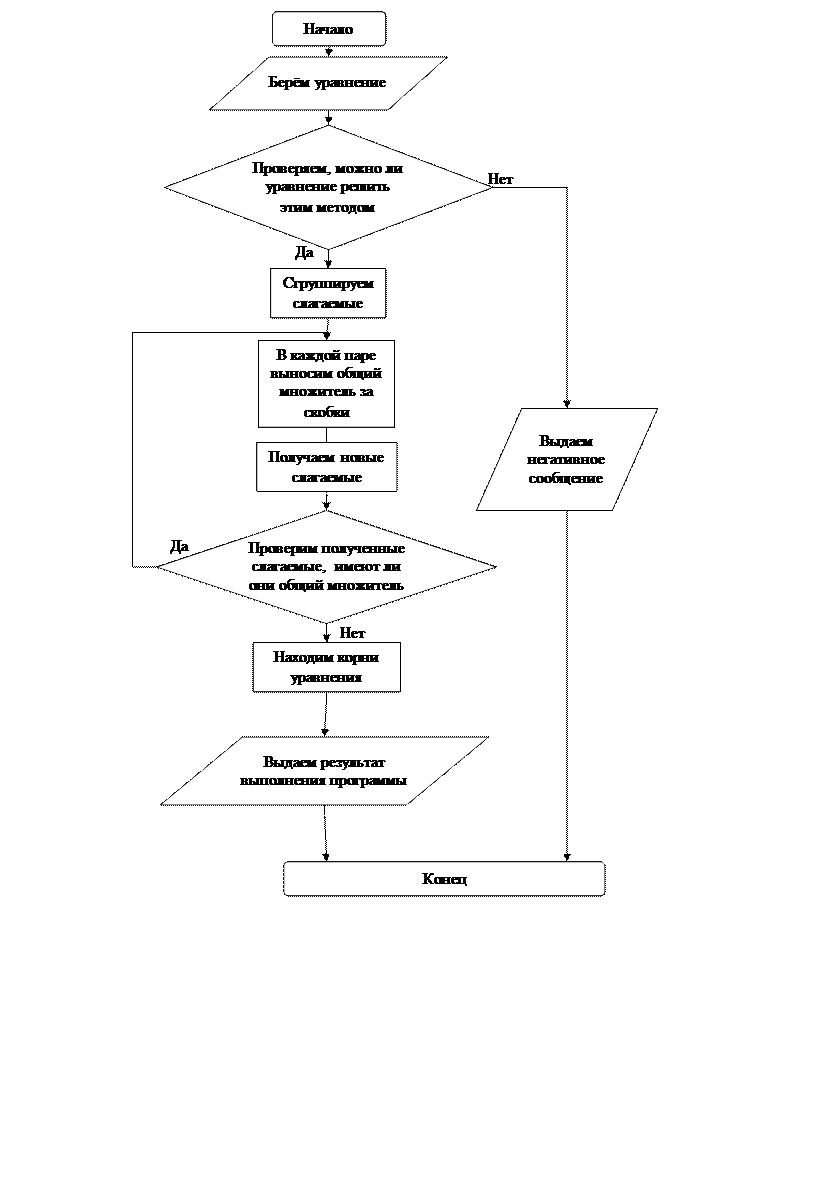
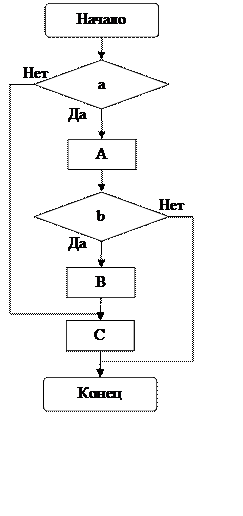
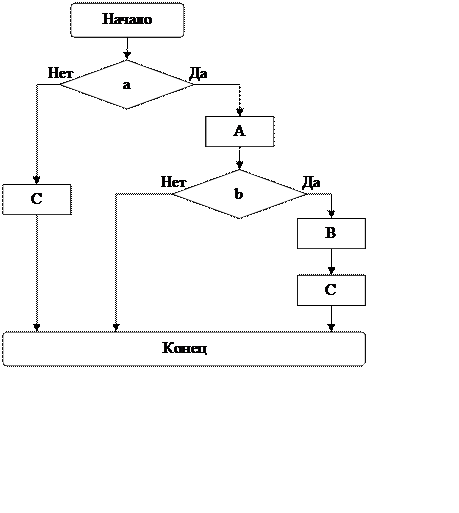
Блок-схема программы: а) способ группировки разложение на множители
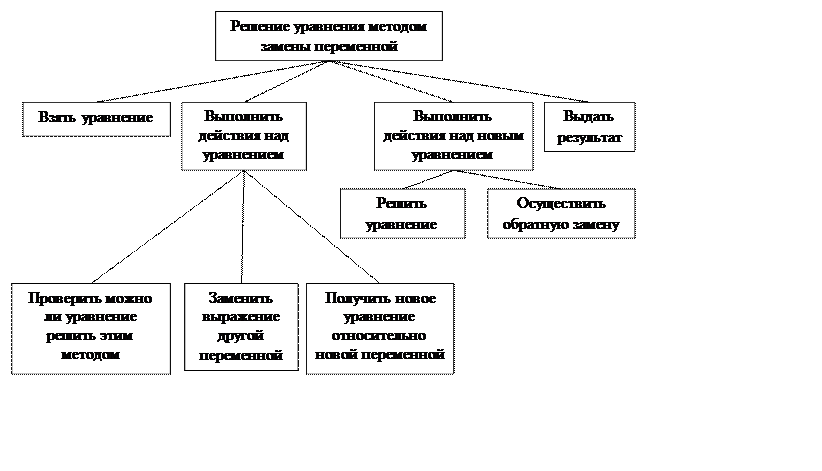
Структурная схема программы: б) замены переменной
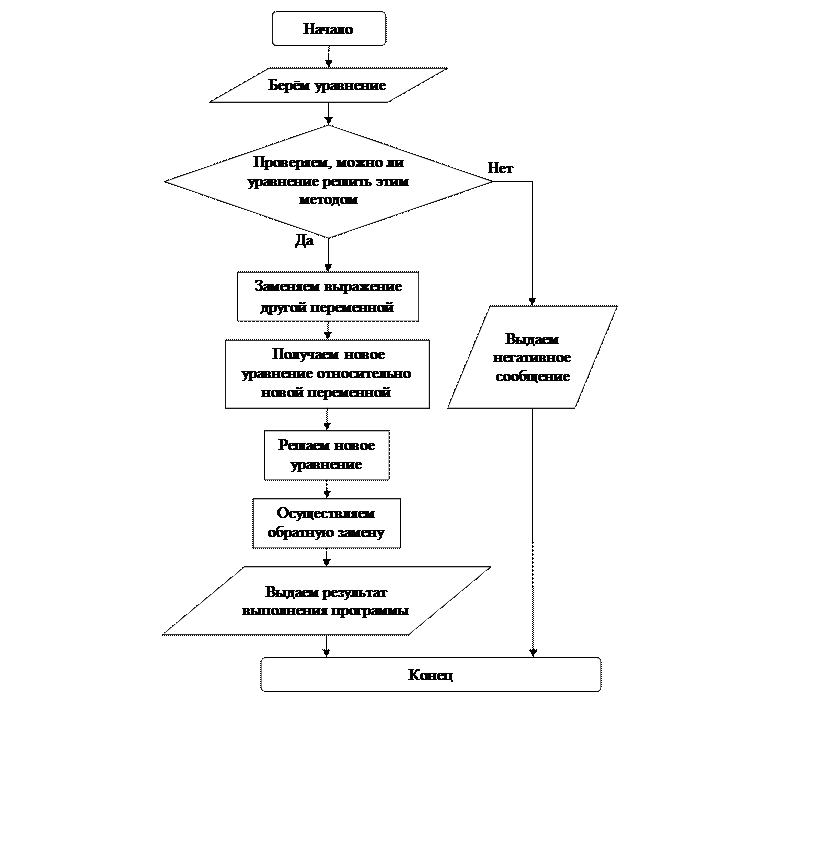
Блок-схема программы: б) замены переменной
Д/З:
Дано: Решение:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.