Численное интегрирование функций: Методические указания к выполнению лабораторной работы № 10

Лабораторная работа № 10

Численное интегрирование функций

Цель работы:           Научиться находить определенный интеграл функции методами прямоугольников, трапеций и парабол.

Содержание отчета

1.  Постановка задачи. Исходные данные.

2.  Анализ решения задачи. Алгоритм решения (блок – схема алгоритма).

3.  Текст программы.

4.  Результат выполнения программы.

5.  Выводы по работе.

Постановка задачи

1.  Найти определенный интеграл функции f(x) на отрезок [a; b]  (данные см. в работе №8) используя метод прямоугольников, трапеций и парабол (метод Симпсона). Количество элементарных отрезков принять N=100.

2.  Полученные данные вывести в следующем виде:

Аналитический расчет:  ***

Расчет методом прямоугольников: ***        Погрешность:  ***

Расчет методом трапеций:        ***       Погрешность:  ***

Расчет методом Симпсона:        ***       Погрешность:  ***

3.  Анализируя полученные значения сделать выводы о точности каждого метода.

Краткие теоретические сведения

Задача численного интегрирования состоит в следующем: найти определенный интеграл на заданном отрезке [a; b], если известна подынтегральная функция (обычно функция задается таблично). Формулы приближенного интегрирования называют квадратурными формулами. Простейшими из них являются: метод прямоугольников, метод трапеций, метод парабол (метод Симпсона). Существуют и более сложные методики, обеспечивающие более высокую точность интегрирования (квадратурные формулы Чебышева, Гаусса и т.д.).

Исходными данными для задачи являются:

1.  Подынтегральная функция y = f(x)

2.  Отрезок [a, b]

3.  Количество элементарных участков N (или шаг интегрирования h).

Метод прямоугольников

Суть метода прямоугольников заключается в следующем. Пусть задана некоторая функция f(x) для которой необходимо найти определенный интеграл на участке [a, b]. Разобьем данный участок на n равных промежутков. На каждом участке примем значение функции постоянным и равным ее значению в начале, середине либо в конце промежутка. В зависимости от приближения, методы носят названия левых, средних либо правых прямоугольников.

Нахождение интеграла в данном случае сводится к нахождению площади полученных прямоугольников. Например, для метода левых прямоугольников, получим формулу:

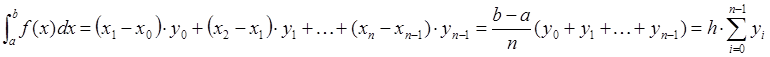
где h – шаг интегрирования.

Алгоритм нахождения интеграла методом прямоугольников:

1.  Присвоить начальные значения: a:= …; b:= …; N:= …;

2.  Рассчитать шаг интегрирования: h:= (b-a)/N

3.  Для I от 0 до N-1 выполнить S:= S + F(a + h*i)

4.  Рассчитать интеграл: S:= S*h т

5.  Вывести результат S

Метод трапеций

Заменим на отрезке [a, b] дугу графика подынтегральной функции f(x) стягивающей ее хордой и вычислим площадь получившейся трапеции. Примем значение определенного интеграла численно равным площади этой трапеции:

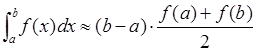
Точность вычислений возрастает, если отрезок [a, b] разделить на несколько частей и применить формулу трапеций для каждого отрезка. Для простоты вычислений удобно делить на равные отрезки. В этом случае численное значение интеграла будет определяться:

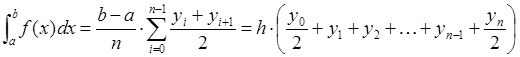
где h = (b-a)/n – шаг интегрирования.

Алгоритм нахождения интеграла методом трапеций:

1.  Присвоить начальные значения: a:= …; b:= …; N:= …;

2.  Рассчитать шаг интегрирования: h:= (b-a)/N

3.  Рассчитать начальное значение S: S:= (f(a) + f(b))/2

4.  Для I от 1 до N-1 выполнить S:= S + F(a + h*i)

5.  Рассчитать интеграл: S:= S*h

6.  Вывести результат S

Метод Симпсона

Данный метод дает заметно более высокую точность по сравнению с методами прямоугольников и трапеций. Кроме того, является довольно простым и удобным для программирования.

Суть метода заключается в том, что подынтегральная функция y = f(x) на отрезке [a; b] заменяется квадратичной функцией. В качестве интерполяционного многочлена используется многочлен Ньютона. Исходя из этого, получим выражение:

.                 

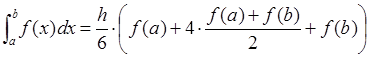Для увеличения точности вычислений отрезок [a; b] разбивают на n пар участков и, заменяя подынтегральную функцию интерполяционным многочленом Ньютона второй степени, получают приближенное значение интеграла на каждом участке длины 2h:

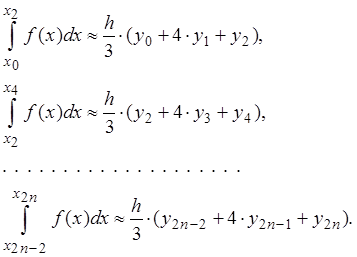
Тогда численное значение определенного интеграла на отрезке [a; b] будет равно сумме интегралов, т.е.

,

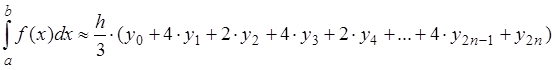где  .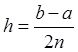

Данное соотношение называется общей формулой Симпсона.

Блок-схема алгоритма нахождения интеграла методом Симпсона:

Методические указания

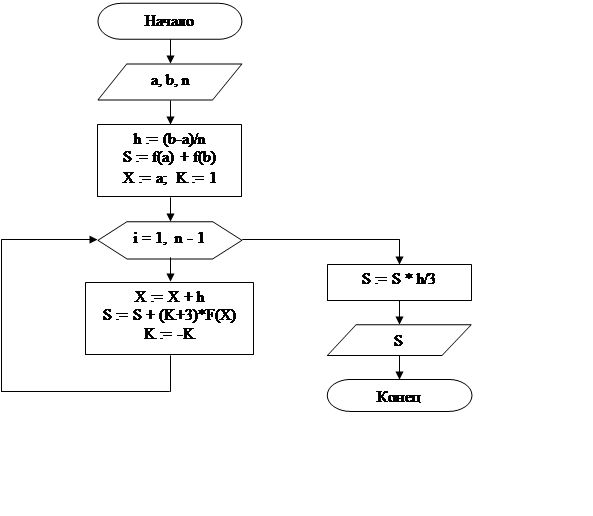
4.  Удобно оформить расчеты с помощью каждого метода в виде отдельной функции. В этом случае заголовок такой функции будет иметь приблизительно такой вид:

Function Integral(a, b: real; N: integer): real;

, где a, b – диапазон интегрирования,

            N – количество отрезков.

5.  Для расчета погрешности каждого метода необходимо заранее произвести аналитический расчет определенного интеграла и задать его значение в программе в виде константы. Погрешность находится следующим образом: E = |Ian - Iras|, где Ian – аналитическое значение интеграла, Iras – расчетное.

Контрольные вопросы

1.  В чем заключается математическая постановка задачи интегрирования функции?

2.  Геометрический смысл различных методов интегрирования.

3.  Преимущества и недостатки каждого метода интегрирования.

4.  От чего зависит точность расчета интеграла?

5.  Как на практике оценивается погрешность каждого из методов?