Численное решение нелинейных уравнений: Методические указания к выполнению лабораторной работы № 9

Лабораторная работа № 9

Численное решение нелинейных уравнений

Цель работы:           1. Практическое исследование методов численного решения нелинейных уравнений.

                                        2. Получения практических навыков работы с системой Turbo Pascal 7.0, закрепление знаний относительно использования функций.

Содержание отчета

1.  Постановка задачи. Исходные данные.

2.  Анализ решения задачи. Алгоритм решения (блок – схема алгоритма).

3.  Текст программы.

4.  Результат выполнения программы.

5.  Выводы по работе.

Постановка задачи

1. Используя исходные данные лабораторной работы №8, а также данные таблицы 9.1, уточнить корень уравнения f(x)=0 на заданном интервале [a; b] с точностью 0.00001.

Таблица 9.1

Вариант	Метод нахождения корня	Вариант	Метод нахождения корня
1 – 3	Половинного деления, метод касательных	16 – 18	Половинного деления, метод хорд
4 – 6	Метод хорд, метод комбинированный метод	19 – 21	Метод хорд, метод касательных
7 – 9	Половинного деления, метод хорд	22 – 24	Половинного деления, метод касательных
10 – 12	Метод хорд, метод касательных	25 – 27	Метод хорд, комбинированный метод
13 – 15	Половинного деления, комбинированный метод	28 – 30	Половинного деления, комбинированный метод

2. Результатом работы программы являются:

1) Значение корня уравнения f(x)=0.

2) Количество произведенных итераций для каждого из указанных методов.

3. По результатам работы сделать выводы о преимуществах и недостатках каждого из используемых методов.

Краткие сведения из теории

Для определения корней алгебраических и трансцендентных уравнений разработаны численные методы,  основанные на уточнении значения корня в предположении,  что на отрезке [A..B] функция Y=F(x) непрерывна и имеет только один корень.  В этом случае значения функции на концах отрезка имеют разные знаки.

Метод половинного деления

Одним из распространенных и простых методов является метод половинного деления  (дихотомии). Он состоит в последовательном делении пополам отрезка, где находится корень. При этом анализируется изменение знака функции на половинах отрезка, и одна из границ отрезка [A..B] переносится в его середину.  Переносится та граница,  со стороны которой функция на половине отрезка знака не меняет. Процесс повторяется до тех пор, пока длина интервала [A..B] не станет меньше заданной погрешности  E  нахождения корня.

Исходными данными для программы являются:

1)  Заданная функция F(X) уравнения F(x) = 0.

2)  Отрезок [A..B] на котором находится единственный корень.

3)  Погрешность нахождения корня E.

Алгоритм программы нахождения корня уравнения методом половинного деления  имеет следующий вид:

1.  Присвоить начальные значения промежутка: a:= …; b:= …

2.  Найти приближенное значение корня: X:= (a + b)/2

3.  Если F(a)*F(X)>0 то a:= x иначе b:= x

4.  Если (b – a) > E то перейти к п.2

5.  Вывести значение X.

Преимуществом данного метода является простота алгоритма и минимальное количество математических расчетов. Наряду с этим, использование метода не всегда целесообразно  в связи с большим количеством итераций (циклов уточнения корня). В этом случае пользуются другими методиками.

Метод хорд

Одним из распространенных методов решения алгебраических и трансцендентных уравнений является метод хорд («метод ложного положения», «метод линейного интерполирования»).

Идея метода заключается в том, что на достаточно малом промежутке [a; b] дуга кривой y=f(x) заменяется стягивающей ее хордой. В качестве приближенного значения корня принимается точка пересечения хорды с осью OX.

Искомое значение x находится по формуле:

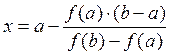
Эта формула носит название формулы метода хорд. Если значение корня x нас не устраивает, то его можно уточнить. Для этого необходимо уменьшить отрезок [a; b] по следующему алгоритму: если знак функции в точке a совпадает со знаком в точке x, т. е. f(a)*f(x)>0, то сдвигаем точку a (a = x), иначе сдвигаем точку b (b=x). Затем применяем метод хорд к новому участку [a; b] и т.д. Процесс необходимо продолжать до тех пор, пока полученное значения корня не будет удовлетворять заданной точности.

Для оценки точности можно использовать формулу ε<=|X_n-X_n-1|, где X_n и X_n-1 приближения корня, полученные на n и n-1 шагах.

Исходные данные для программы те же, что для предыдущей задачи.

Алгоритм программы нахождения корня уравнения методом хорд  имеет следующий вид:

1.  Присвоить начальные значения промежутка: a:= …; b:= …

2.  Принять начальное значение корня: X:= a

3.  Сохранить старое значение корня: Xo:= X

4.  Найти новое приближенное значение корня: X:= a-F(a)*(b-a)/(F(b)-F(a))

5.  Если F(a)*F(X)>0 то a:= x иначе b:= x

6.  Если |X – Xo| > E то перейти к п.3

7.  Вывести значение X.

Преимуществом метода хорд является сравнительно меньшее количество итераций, чем в методе половинного деления.

Метод Ньютона (метод касательных)

Геометрический смысл метода Ньютона состоит в том, что дуга кривой y=f(x) заменяется касательной к этой кривой (отсюда и второе название метода). В этом случае, уточненное значение корня рассчитывается по формуле:

.

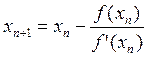При выборе начального приближения необходимо руководствоваться правилом: за исходную точку следует выбирать тот конец отрезка [a, b], в котором знак функции совпадает со знаком второй производной:

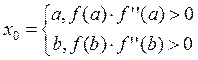
Уточнения проводятся до тех пор, пока не выполнится условие |X_n-X_n-1|<=ε.

Алгоритм программы нахождения корня уравнения методом касательных