Перевірка статичних гіпотез для однієї та двох вибірок при введенні трьох послідовностей з 50, 75, 100 цілих чисел діапазоном 1-30 з різними частотами появи

Виконав: Половинко Сергій КИТ-14б

Лабораторна робота № 2

Тема: Перевірка статичних гіпотез.

Мета: Перевірка статичних гіпотез для однієї та двох вибірок.

Хід виконання:

1.Вводимо три послідовності з 50, 75, 100 цілих чисел діапазоном 1-30 з різними частотами появи:

4

6

10

5

4

3

1

11

12

4

10

14

7

2

9

13

15

4

3

8

Побудував гістограму та графік:

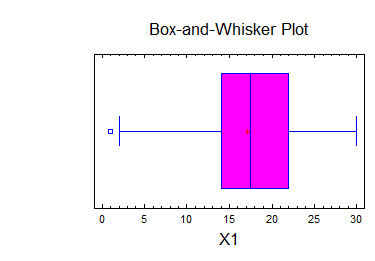
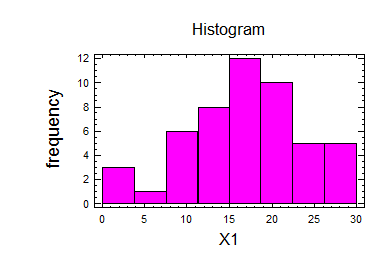
2.Використовуючи опцію “Summary Statistic” визначаємо основні статистичні параметри заданої величини Х:

Математичне очікування = 17,16

Дисперсія  = 47,9739

Аналітично визначимо основні статистичні характеристики і порівняємо їх з розрахунками, що отримали за допомогою пакета Statgraphics:

Розрахунки:

Кількість = 20

Математичне очікування = 7.25

Медіана = 6.5

Мода = 4

Середнє геометричне = 5.8883

Дисперсія = 18.19736

Стандартне відхилення = 4.26584

Стандартна помилка = 0.95387

Мінімум = 1

Максимум = 15

Діапазон = 14

Нижній квартиль = 4

Верхній квартиль = 10.5

Межквартальний діапазон = 6.5

Коефіцієнт асиметрії = 0.3596256

Стандартизований коефіцієнт асиметрії = 0.6565836

Коефіцієнт ексцесу = -1.13521

Стандартизований коефіцієнт ексцесу = -1.0363058

Коефіцієнт варіації = 58.8391%

Сума = 145

3.Будуємо для отриманої послідовності чисел гістограму і полігон частот та кумулятивну криву:

Гістограма частот:                                                              Полігон частот:

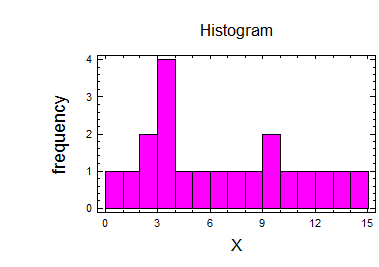
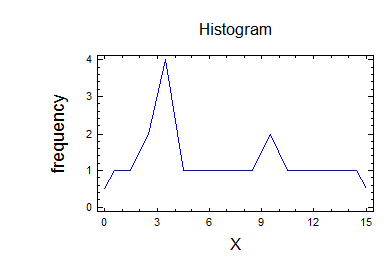
Кумулятивна крива:

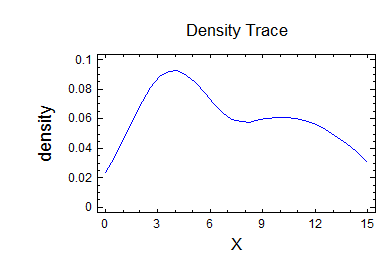
4. Будуємо графіки наступних розподілів згідно індивідуального завдання.

Нормальний розподіл. Для побудови графіків розподілів необхідно обрати у вікні “Probability Distributions” потрібний розподіл та натиснути «ОК». Натиснути праву кнопку у вікні графіка та обрати пункт “Analysis Options”, ввести необхідні параметри.

а) Розподіл ймовірностей неперервної випадкової величини, яке описується диференціальною функцією.

1) Біноміальний розподіл.

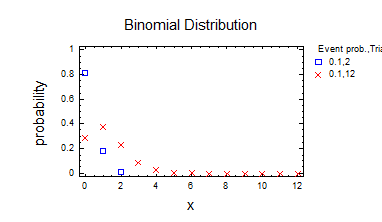
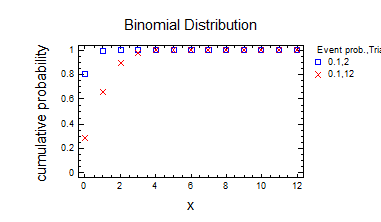
 2) Біноміальний розподіл 2.

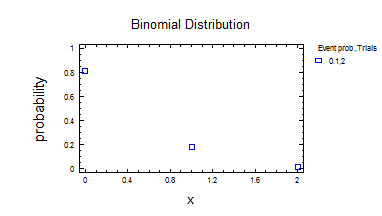
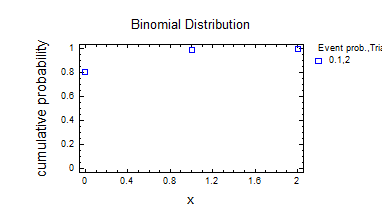
3) Нормальний розподіл.

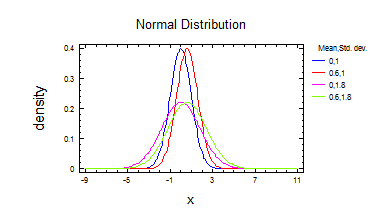
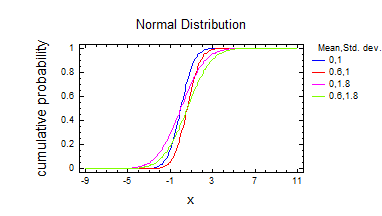
4) Розподілення Хі-квадрат.

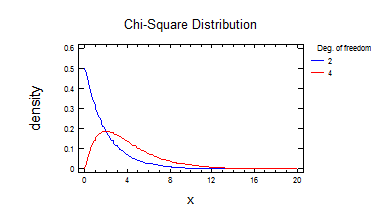
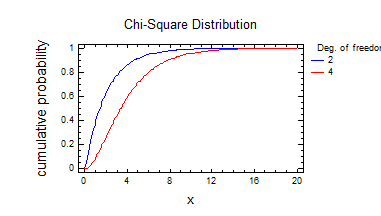
5) Розподілення Хі-квадрат 2.

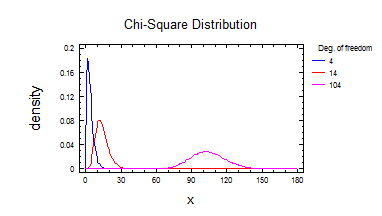
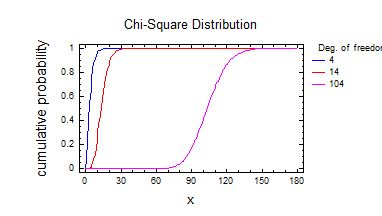
6) Розподілення Хі-квадрат 3.

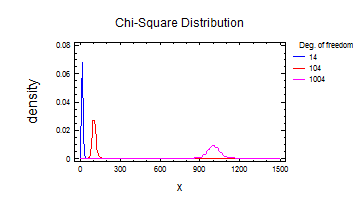
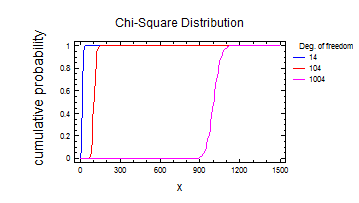
Висновок: зі збільшенням числа степенів свободи розподілення Хі-квадрат наближається до нормального.

7) Розподілення Стьюдента.

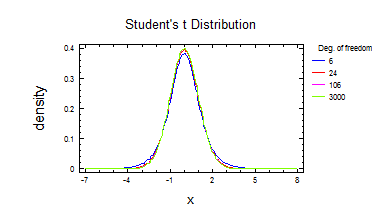
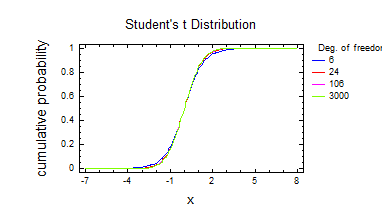
Висновок: зі збільшенням числа степенів свободи графік розподілення Стьюдента наближається до нормального.

8) Розподілення Фішера.

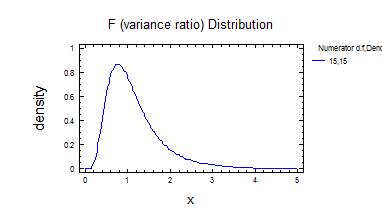
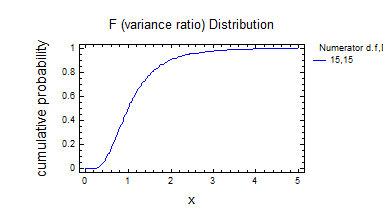
9) Розподілення Фішера 2.

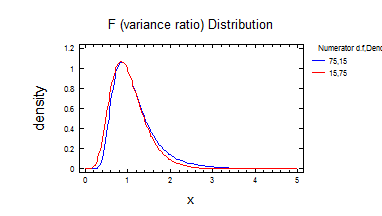
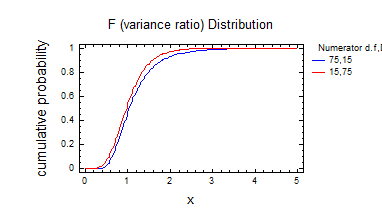
Висновок: при збільшенні степені свободи графік розподілення Фішера наближається до нормального.

Лист розрахунків

	A	B	C	D	E	F	G
1	Xi	(хi-М)^2	(хi-М)^3
2	4	10.563	-34.328		Матиматическое ожидание:	7.250	СУММ(A2:A21)/СЧЁТ(A2:A21)
3	6	1.563	-1.953		Медиана:	6.500	МЕДИАНА(A2:A21)
4	10	7.563	20.797		Мода:	4.000	МОДА(A2:A21)
5	5	5.063	-11.391		Среднее геометрическое:	5.888	СРГЕОМ(A2:A21)
6	4	10.563	-34.328		Дисперсия:	18.197	СУММ(B2:B21)/(СЧЁТ(B2:B21)-1)
7	3	18.063	-76.766		Стандартное отклонение:	4.266	КОРЕНЬ(F6)
8	1	39.063	-244.141		Стандартная ошибка:	0.954	F7/КОРЕНЬ(СЧЁТ(A2:A21))
9	11	14.063	52.734		Минимум:	1.000	МИН(A2:A21)
10	12	22.563	107.172		Максимум:	15.000	МАКС(A2:A21)
11	4	10.563	-34.328		Диапазон:	14.000	F10-F9
12	10	7.563	20.797		Нижний квартиль:	4.000	КВАРТИЛЬ(A3:A21;1)
13	14	45.563	307.547		Верхний квартиль:	10.500	КВАРТИЛЬ(A3:A21;3)
14	7	0.063	-0.016		Межквартильный диапазон:	6.500	F13-F12
15	2	27.563	-144.703		Коэффициент ассиметрии:	0.360	(СЧЁТ(A2:A21)*СУММ(C2:C21))/((СЧЁТ(A2:A21)-1)*(СЧЁТ(A2:A21)-2)*СТЕПЕНЬ(F7;3))
16	9	3.063	5.359		СКА:	0.657	F15/КОРЕНЬ(6/СЧЁТ(A2:A21))
17	13	33.063	190.109		КЭ:	-1.135	ЭКСЦЕСС(A2:A21)
18	15	60.063	465.484		СКЭ:	-1.036	F17/КОРЕНЬ(24/СЧЁТ(A2:A21))
19	4	10.563	-34.328		КВ:	58.839	(F7/F2)*100
20	3	18.063	-76.766		Сумма:	145.000	СУММ(A2:A21)
21	8	0.563	0.422