Информатика и выч. техника \ Планирование эксперимента и обработка экспериментальных данных

Планування повного факторного експерименту

Страницы работы

4 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Лабораторна робота №8-9

Тема: Планування повного факторного експерименту.

Мета: Навчитися виконувати планування повного факторного експерименту з використанням пакету Statgraphics.

Опис ходу виконання:

Для побудови плану експерименту необхідно визначити точки в факторному просторі, в яких треба виконувати виміри. Користуючись таблицею 2 у вказівках до лабораторної роботи та програмою EExp, отримуємо наступний вигляд плану:

Х0	Х1	Х2	Х3	У
1	-1	-1	-1	15,92
1	1	-1	-1	61,67
1	-1	1	-1	-101,89
1	1	1	-1	-312,27
1	-1	-1	1	-34,72
1	1	-1	1	74,38
1	-1	1	1	84,64
1	1	1	1	-151,03
2	-1	-1	-1	15,22
2	1	-1	-1	57,85
2	-1	1	-1	-100,7
2	1	1	-1	-316,17
2	-1	-1	1	-34,14
2	1	-1	1	78,42
2	-1	1	1	88,15
2	1	1	1	-159,25
3	-1	-1	-1	15,82
3	1	-1	-1	56,56
3	-1	1	-1	-103,1
3	1	1	-1	-313,39
3	-1	-1	1	-35,24
3	1	-1	1	74,11
3	-1	1	1	82,97
3	1	1	1	-152,62
4	-1	-1	-1	16,55
4	1	-1	-1	56,35
4	-1	1	-1	-100,08
4	1	1	-1	-311,49
4	-1	-1	1	-34,63
4	1	-1	1	79,45
4	-1	1	1	85,15
4	1	1	1	-152,09
5	-1	-1	-1	15,51
5	1	-1	-1	61,35
5	-1	1	-1	-102,6
5	1	1	-1	-312,6
5	-1	-1	1	-33,52
5	1	-1	1	76,62
5	-1	1	1	86,77
5	1	1	1	-156,26

Далі необхідно перевірити неоднорідність дисперсій (перевірка відтворення експериментів). Виконується лише в тому випадку, коли кількість експериментів в кожній точці плану > 1. Для перевірки неоднорідності дисперсій перевіряється наступна гіпотеза:

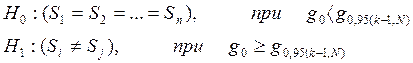
Для перевірки гіпотези використовується критерій Кохрена. Для кожного досліду знаходиться сума квадратів помилок за формулою: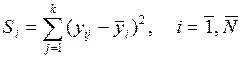

Таблиця 2.

	Х0	Х1	Х2	Х3	Х1Х2	Х2Х3	Х1Х3	Х1Х2Х3	У1	У2	У3	У4	У5	y_c_р	S_i
1	+	-	-	-	+	+	+	-	15,92	15,22	15,82	16,55	15,51	15.8	0.99
2	+	+	-	-	-	+	-	+	61,67	57,85	56,56	56,35	61,35	58.76	26.64
3	+	-	+	-	-	-	+	+	-101,89	-100,7	-103,1	-100,08	-102,6	-101.67	6,4272
4	+	+	+	-	+	-	-	-	-312,27	-316,17	-313,39	-311,49	-312,6	-313.18	13
5	+	-	-	+	+	-	-	+	-34,72	-34,14	-35,24	-34,63	-33,52	-34.45	1,69
6	+	+	-	+	-	-	+	-	74,38	78,42	74,11	79,45	76,62	76.6	22,5
7	+	-	+	+	-	+	-	-	84,64	88,15	82,97	85,15	86,77	86.53	20,82
8	+	+	+	+	+	+	+	+	-151,03	-159,25	-152,62	-152,09	-156,26	-154.25	46,72

Також находиться сума квадратів помилок вимірювань:

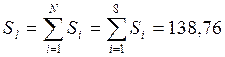
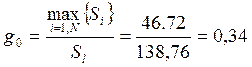
Оскільки 0,34<0,391, то приймається основна гіпотеза і продовжуємо проведення експерименту.

Далі неохідно розрахувати коефіцієнти математичної моделі за методом найменших квадратів:

Скористуємось пакетом Derive:

З отриманих значень видно, що рівняння прийме наступний вигляд:

У=-45,86-37,16*х1-75,03*х2+39,215*х3-75,66*х1х2+47,32*х2х3+4,9*х1х3-12,045*х1х2х3

Перевірка статистичної значимості коефіцієнтів виконується за допомогою наступних гіпотез:

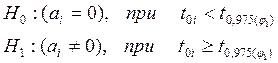
Значення критерію Ст’юдента знаходиться наступним чином:

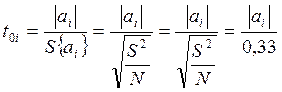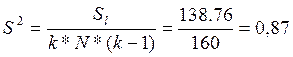
Запишемо дані в таблицю

Коефіцієнти	Критерій Ст’юдента	Значущість
А0	138.97	Значимий
А1	112.6	Значимий
А2	227,4	Значимий
А3	118,8	Значимий
А12	229,27	Значимий
А13	14,85	Значимий
А23	143,39	Значимий
А123	36,5	Значимий