Информатика и выч. техника \ Планирование эксперимента и обработка экспериментальных данных

Встановлення статистичного зв’язку між сукупностями даних. Вивчення та застосування рангових коефіцієнтів кореляції

Страницы работы

Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ.

Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.

Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.

Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.

Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.

Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.

Содержание работы

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НТУ «ХПІ»

Кафедра обчислювальної техніки та програмування

ЗВІТ З ЛАБОРАТОРНОЇ РОБОТИ № 4

З КУРСУ: «ПЛАНУВАННЯ ЕКСПЕРИМЕНТУ ТА ОБРОБКА ЕКСПЕРИМЕНТАЛЬНИХ ДАНИХ»

Виконав студент

гр. КІТ -14в

Марченко В.Ю.

Перевірив:

Черних О.П.

Харків 2006

Кореляційний аналіз.

Мета роботи: отримання практичних навичток по встановленню статистичного зв’язку між сукупностями даних. Вивчення та застосування рангових коефіцієнтів кореляції.

Порядок виконання роботи:

Дослід№1

Вводимо дві послідовності (x,y) з n=10 чисел згідно з варіантом №1.

X={4,5,6,8,3,1,9,10,2,7}

Y={5,6,4,8,2,3,10,9,1,7}

2. У процедурному блоці Decribe- Numeric Data – Multiple Variable Analysis вибираємо 2 змінні у полі Data. У Tabular Options обираємо Corellations та Rank Corellations

Multiple-Variable Analysis

Correlations

X Y

------------------------------------------------

X 0,9152

( 10)

0,0002

Y 0,9152

( 10)

0,0002

------------------------------------------------

Spearman Rank Correlations

X Y

------------------------------------------------

X 0,9152

( 10)

0,0060

Y 0,9152

( 10)

0,0060

Kendall Rank Correlations

X Y

------------------------------------------------

X 0,7778

( 10)

0,0017

Y 0,7778

( 10)

1,0000

------------------------------------------------

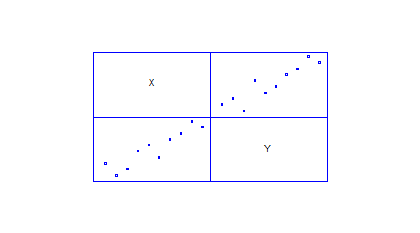
Розрахуємо коефіцієнти кореляції

Коефіцієнт Пірсона:

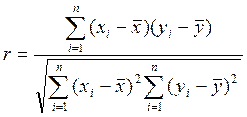= 0.9152

>> x=[4 5 6 8 3 1 9 10 2 7];

>> y=[5 6 4 8 2 3 10 9 1 7];

>> x_=x-(sum(x)/10);

>> y_=y-sum(y)/10;

>> r1=sum(x_.*y_)

r1 = 75.5000

>> r2=sqrt(sum((x_).^2)*sum((y_).^2))

r2 = 82.5000

>> rez=r1/r2

rez = 0.9152

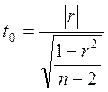= 6.4233

>> t=rez/sqrt((1-rez^2)/(10-2))

t =6.4233

Перевіряємо значущість коефіцієнта:

при

=6.4233

=2.30601

Коефіцієнт Спірмена:

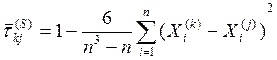= 0.9152

>> x=[4 5 6 8 3 1 9 10 2 7];

>> y=[5 6 4 8 2 3 10 9 1 7];

>> sp=(x-y).^2;

>> spirman=1-((6/(10^3-10))*sum(sp))

spirman =0.9152

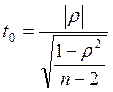= 6.4233

>> t= spirman /sqrt((1- spirman ^2)/(10-2))

t =6.4233

Перевіряємо значущість коефіцієнта:

при

=6.4233

=2.30601

Коефіцієнт Кендела:

Впорядкуємо послідовність:

>> x=[4 5 6 8 3 1 9 10 2 7];

>> y=[5 6 4 8 2 3 10 9 1 7];

1	2	3	4	5	6	7	8	9	10
3	1	2	5	6	4	7	8	10	9

V12=V13=1 V14= V15= V16= V17= V18= V19= V110=0

V21= V22= V23= V24= V25= V26= V27= V28= V29= V210=0

V34= V35= V36= V37= V38= V39= V310=0

V46=1 V45= V47= V48= V49= V410=0

V56=1 V57= V58= V59= V510=0

V67= V68= V69= V610=0

V78= V79= V710=0

V89= V810=0

V910=1

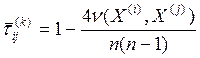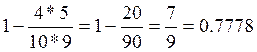
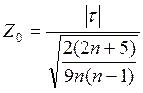=0.0348

>> 0.7778/sqrt(2*(10*2+5)/9*10*(10-1))

ans = 0.0348

Перевіряємо значущість коефіцієнта:

при

=0.0348

=1.95997

Дослід№2

Вводимо дві послідовності (x,y) з n=10 чисел згідно з варіантом №1.

X={3,3,3,4,5,1,5,2,6,7}

Y={3,4,4,3,3,4,2,5,1,2}

Correlations

X Y

------------------------------------------------

X -0,8465

( 10)

0,0020

Y -0,8465

( 10)

0,0020

------------------------------------------------

Spearman Rank Correlations

X Y

------------------------------------------------

X -0,8893

( 10)

0,0076

Y -0,8893

( 10)

0,0076

------------------------------------------------

Kendall Rank Correlations

X Y

------------------------------------------------

X -0,7854

( 10)

0,0056

Y -0,7854

( 10)

1,0000

------------------------------------------------

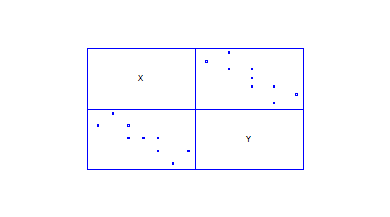
Розрахуємо коефіцієнти кореляції:

Коефіцієнт Пірсона:

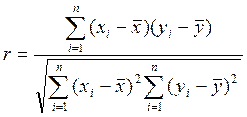= -0,7854

>> x=[3 3 3 4 5 1 5 2 6 7];

>> y=[3 4 4 3 3 4 2 5 1 2];

>> x_=x-(sum(x)/10);

>> y_=y-sum(y)/10;

>> r1=sum(x_.*y_)

r1 =-16.9000

>> r2=sqrt(sum((x_).^2)*sum((y_).^2))

r2 =19.9652

>> rez=r1/r2

rez =-0.8465

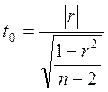= -4,4967

>> t=rez/sqrt((1-rez^2)/(10-2))

t = -4.4967

Перевіряємо значущість коефіцієнта:

при

при - правильна гіпотеза

t₀=-4,4967

t_0,975(т-2)=2,30601

Коефіцієнт Спірмена:

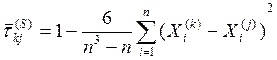=-0,7854

>> x=[3 3 3 4 5 1 5 2 6 7];

>> y=[3 4 4 3 3 4 2 5 1 2];

>> sp=(x-y).^2;

>> spirman=1-((6/10^3-10))*sum(sp))

spirman=-0,7854

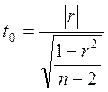=--4,4967

>> t=spirman/sqrt((1-spirman^2)/(10-2))

t= - 4,4967

Перевіряємо значущість коефіцієнта:

при

при - правильна гіпотеза

t₀=- 4,4967

t_0,975(т-2)=2,30601

Коефіцієнт Кендела:

Впорядковуємо послідовність:

>> x=[3 3 3 4 5 1 5 2 6 7];

>> y=[3 4 4 3 3 4 2 5 1 2];

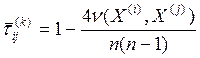=-0,8893

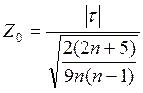= -0.0398

>> -0.8893/sqrt(2*(10*2+5)/9*10*(10-1))

ans = -0.0398

Перевіряємо значущість коефіцієнта:

при --- правильна гіпотеза

при

=-0.0398

=1,95997

Висновок: отримали практичні навички по встановленню статистичного зв’язку між сукупностями даних. Вивчили та застосування рангових коефіцієнтів кореляції