Дослідження залежності даних за допомогою лінійного регресійного аналізу

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НТУ «ХПІ»

Кафедра обчислювальної техніки та програмування

ЗВІТ З ЛАБОРАТОРНОЇ РОБОТИ № 5

З КУРСУ: «ПЛАНУВАННЯ ЕКСПЕРИМЕНТУ ТА ОБРОБКА ЕКСПЕРИМЕНТАЛЬНИХ ДАНИХ»

Виконав студент

гр. КІТ -14в

Марченко В.Ю.

Перевірив:

Черних О.П.

Харків 2006

Лабораторна робота № 3

Тема: Лінійний регресійний  аналіз

Мета: Дослідження залежності даних за допомогою лінійного регресійного аналізу.

ХІД РОБОТИ:

Маємо слідуючи вхідні та вихідні дані:

                      Рис.1. – дані за варіантом

За допомогою процедури Relate пакету дослідження  заданої залежності. Маємо:

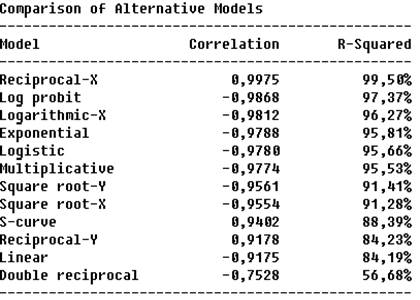
Потрібно вибрати найкращу та другу за найкращою моделі. Це Reciprocal-X та Logarithmic-X.

Маємо графіки цих функцій:

       

  

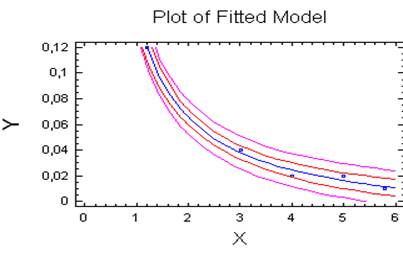
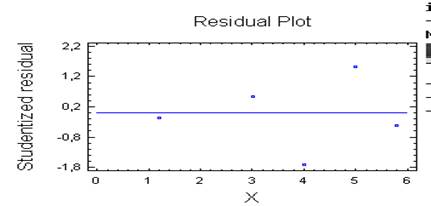
Рис.2. – зрівняння з графіком функції зворотня відносно Х (Reciprocal-X)

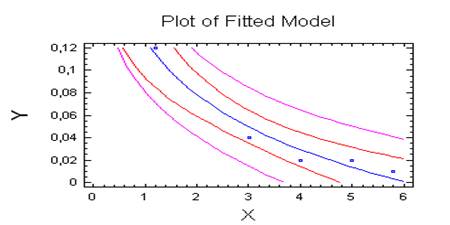
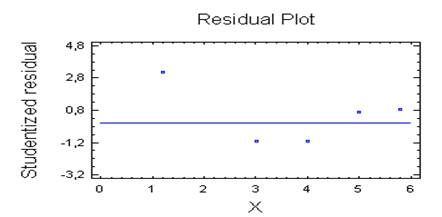
Рис.3. – зрівняння з графіком функції логарифмічна Logarithmic-X.

Розрахуємо для найкращої моделі оцінку параметрів регресії, дисперсію та  кореляційний коефіцієнт:

1.Найкраща модель Reciprocal –X залежність має вигляд:

Тобто якщо лінійне рівняння має вигляд У=А+ВХ, де Х-матриця плана, У-вихідні значення , Ата В – невідомі коефіцієнти, то для нашого випадку

 У=у, А=а, В=b, Х=х.

Вимірювання проводяться у п’яти точках:

х₁=1,2             х₂=3            х₃=4           х₄= 5          х₅=5,8

Значення у приймають значення:

_у1= 0,12              у₂= 0,04                 у₃=0,02                у₄=0,02               у₅=0,01

Виконаємо розрахунок параметрів регресії:

Находим X^TX:                                                          

            1        0,83

                                                                                  1      0,33                   5          1,78

                1        1        1          1         1                     1       0,25         =                                     

X^TX =                                                            .          1      0,2                    1,78      0,93

    0,83  0,33  0,25    0,2     0,17                     1     0,17

 

0,63            - 1,2

(X^TX)^-1=          - 1,2             3,38

0,12

                                                                           0,04

Х^Ту=        1             1            1           1         1              0,02        =   0,21

                                                                      .   0,02          0,12

     0,83     0,33       0,25        0,2      0,17           0,01

Визначаємо  а=(Х^ТХ)^-1Х^Ту

       0,63        -1,2              0,21              - 0,01

а=                             .             =

       -1,2         3,38              0,12               0,15

З цього виходить а₀ = -0,01       а₁=0,15

Модель  має вигляд  у= - 0,01 + 0,15 (1/х), маємо невеливе відхилення  від отримання моделі за допомогою пакета – у= -0,0168097 + 0,164357/х

Визначимо довірчий інтервал для а₀  та а₁. Для цього потрібно знайти оцінку дисперсії. Для цього знайдем:

                 0,12              1     0,83                            0,005

                  .....               1     0,33          -0,01              0

                                -     1    0,25     .           =  - 0,0075

                 ......               1     0,2              0,15            0

                                      1     0,1                             - 0,0059

у-Ха=       .....                      

     0,01

d=0,00013/3=0,00004

∆а₁=t_0.975(4)* √d(X^TX)^-1_n

Так як t_0.975(4)=3.182, то ∆а₀=+3,182√0,00004*0,63= 0,016

Тобто ∆а₀= - 0,01+0,016, а ∆а₁=0,15+0,037

Розраховуємо  коефіцієнт кореляції:

Х=3,8   та Y=0.042

Підставимо у формулу значення та отримаємо  r=-0,296/0,3226=-0,9176

2.Друга після найкращої моделі Regression Analysis – Logarithmic-X model :

Y=a+b*ln(X)(логарифмічна).

Тобто якщо лінійне рівняннямає вигляд  У=А+ВХ, де Х-матриця плана, У-вихідні значення, А та В – невідомі коефіцієнти, то для нашого випадку

У=у       А=а        В=b         Х=ln(X)

Вимірювання проводяться у п’яти точках:

х₁=1,2             х₂=3            х₃=4           х₄= 5          х₅=5,8

Значення у приймають значення:

_у1= 0,12              у₂= 0,04                 у₃=0,02                у₄=0,02               у₅=0,01

Виконаємо розрахунок параметрів регресії:

Знаходим X^TX:

               1             1           1         1              1              1    0,18

                                                                             *      1    1,1               5     6,04

X^TX =    0,18      1,1       1,39      1,61       1,76            1      1,39    =

                                                                         1     1,61            6,04   8,86

                                                                         1     1,76

                1,13        -0,77

(X^TX)^-1= -0,77         0,64                                                 0,12

          1                1           1            1           1                 0,04          0,21

Х^Ту= 0,18         1,1         1,39       1,61      1,76     *      0,02   =    0,14

                                                                            0,02

  0,01

Визначаємо а=(Х^ТХ)^-1Х^Ту

                                       0,21

1,13           -0,77                                 0,13

а=                                     *                    =

-0,77           0,64              0,14             0,07

З цього виходить  а₀=0,13      а₁=-0,07

Модель має вигляд   у=-0,13 -0,07 ln(X), маємо невелике відхилення від отриманої моделі за допомогою пакета    у=0,127246-0,070632*ln(x).

Визначимо довірчий інтервал для  а₀ та а₁. Для цього потрібно знайти оцінку дисперсії d. Для цього  знайдем :

                                                                          0

             0,12        1      0,18                               -0,01

             ......         1       1,1             0,13            -0,01

 .......        1       1,39   *                 =       0

 ......    -    1       1,61         -0,07             0

у-Ха=   .......        1      1,76

 0,01

d=(y-Xa)^T(y-Xa)/5-1-1=0.000363/3=0.000121

∆а₁=t_0.975(4)* √d(X^TX)^-1_n

Так як  t_0.975(4)=3,182, то ∆а₀=+3,182√0,000121*1,13=0,037

∆а₁=+3,182√0,000121*0,64=0,028

Тобто ∆а₀=0,13+0,037, а ∆а₁=-0,07+0,028

Коефіцієнт кореляції було розраховано вище.

Висновок: у ході лабораторної роботи ми дослідили залежності даних за допомогою лінійного регресійного аналізу.