Лабараторна робота 6
Тема: Нелінійний регресійний аналіз.
Мета: Дослідження залежності даних за допомогою нелінійного регресійного аналізу.
Хід роботи:
Вводимо дані згідно індивідуального завдання:
|
Х |
0,1 |
0,8 |
1,4 |
2 |
3 |
|
у |
0,09 |
0,19 |
0,22 |
0,23 |
0,25 |
Далі обираємо пункт “Relate-Polinomial Regression”та вводимо імена залежної та незалежної змінної. Для побудови необхідних графіків натискаємо на кнопку “Graphical Options”, далі “Plot of Fitted Model” та “Residual versus X”.
Виконаємо дослідження заданої залежності.
Для поліномів 2 ступеню:
Polynomial Regression Analysis
-----------------------------------------------------------------------------
Dependent variable: Y
-----------------------------------------------------------------------------
Standard T
Parameter Estimate Error Statistic P-Value
-----------------------------------------------------------------------------
CONSTANT 0,0849028 0,0175827 4,82876 0,0403
X 0,132484 0,0263481 5,02823 0,0374
X^2 -0,0263708 0,00809077 -3,25937 0,0826
-----------------------------------------------------------------------------
Analysis of Variance
-----------------------------------------------------------------------------
Source Sum of Squares Df Mean Square F-Ratio P-Value
-----------------------------------------------------------------------------
Model 0,0153687 2 0,00768433 27,88 0,0346
Residual 0,000551341 2 0,00027567
-----------------------------------------------------------------------------
Total (Corr.) 0,01592 4
R-squared = 96,5368 percent
R-squared (adjusted for d.f.) = 93,0736 percent
Standard Error of Est. = 0,0166033
Mean absolute error = 0,00891015
Durbin-Watson statistic = 2,55202 (P=0,0000)
Lag 1 residual autocorrelation = -0,354937
The StatAdvisor
---------------
The output shows the results of fitting a second order polynomial
model to describe the relationship between Y and X. The equation of
the fitted model is
Y = 0,0849028 + 0,132484*X-0,0263708*X^2
Since the P-value in the ANOVA table is less than 0.05, there is a
statistically significant relationship between Y and X at the 95%
confidence level.
95,0% confidence intervals for coefficient estimates
-----------------------------------------------------------------------------
Standard
Parameter Estimate Error Lower Limit Upper Limit
-----------------------------------------------------------------------------
CONSTANT 0,0849028 0,0175827 0,00925036 0,160555
X 0,132484 0,0263481 0,0191176 0,245851
X^2 -0,0263708 0,00809077 -0,0611826 0,00844094
Unusual Residuals
--------------------------------------------------------------
Predicted Studentized
Row Y Y Residual Residual
--------------------------------------------------------------
1 0,09 0,0978875 -0,00788748 -3,90
5 0,25 0,245018 0,00498207 2,96
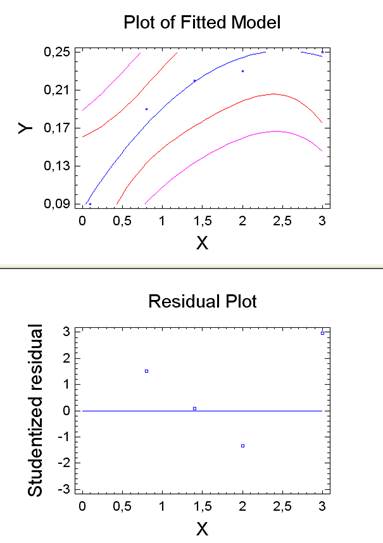
Рисунок 1 Графики для полиномов 2 степени
Для поліномів 3 ступеню виконати дослідження залежності не вдалося.
Для поліномів 4 ступеню:
Polynomial
Regression Analysis
-----------------------------------------------------------------------------
Dependent variable: Y
-----------------------------------------------------------------------------
Standard T
Parameter Estimate Error Statistic P-Value
-----------------------------------------------------------------------------
CONSTANT 0,0667008
X 0,246979
X^2 -0,143525
X^3 0,0369133
X^4 -0,00324168
-----------------------------------------------------------------------------
Analysis of Variance
-----------------------------------------------------------------------------
Source Sum of Squares Df Mean Square F-Ratio P-Value
-----------------------------------------------------------------------------
Model 0,01592 4 0,00398
Residual 0,0 0 0,0
-----------------------------------------------------------------------------
Total (Corr.) 0,01592 4
R-squared = 100,0 percent
R-squared (adjusted for d.f.) = 0,0 percent
Standard Error of Est. = 0,0
Mean absolute error = 0,0
Durbin-Watson statistic = 3,509
Lag 1 residual autocorrelation = -0,765986
Not enough data to compute confidence intervals.
Cannot compute Studentized residuals.
Розрахуємо основні статичні характеристики для поліномів:
Для поліному 2 ступеню:
![]()
![]()
Исходные значения:
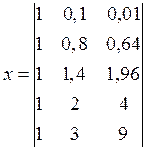
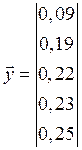
Найдем транспортированную матрицу:
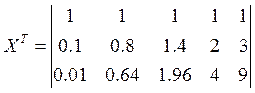
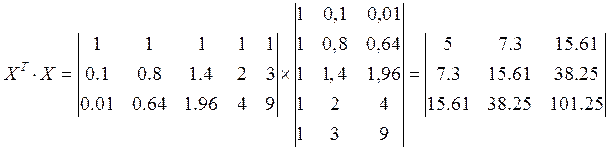
Знаходимо дисперсійну матрицю:
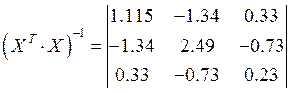
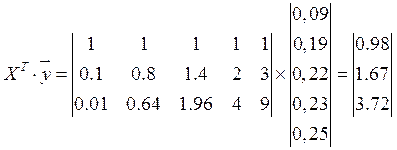
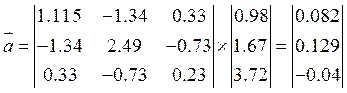
![]()
![]()
![]()
Модель имеет вид:
![]()
Рассчитанная модель немного отличается от полученной в пакете:
Y = 0,0849028 + 0,132484*X-0,0263708*X^2
Знаходимо стандартну помилку для кожної оцінки та кореляційні коефіцієнти, записавши вектор помилок:
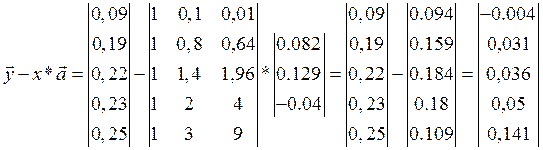
Знаходимо дисперсію:
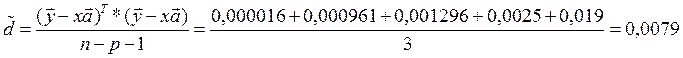
Знаходимо довірюючі інтервали:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Для поліному 3 ступеню:
![]()
![]()
Исходные данные:
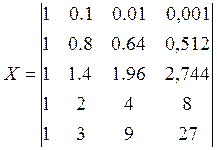
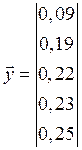
Находим транспонированную матрицу
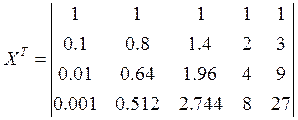
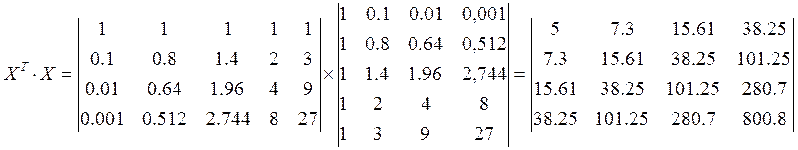
Знаходимо дисперсійну матрицю:
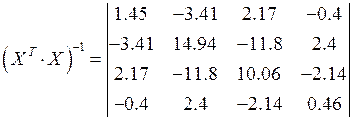
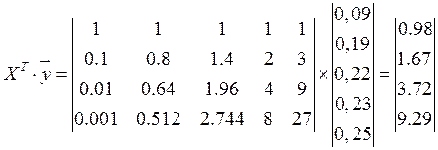
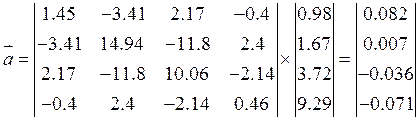
![]()
![]()
![]()
![]()
Модель имеет вид:
![]()
Знаходимо стандартну помилку для кожної оцінки та кореляційні коефіцієнти, записавши вектор помилок:
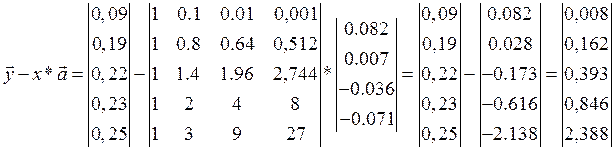
Знаходимо дисперсію:
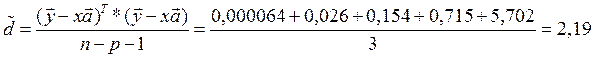
Знаходимо довірюючі інтервали:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.