Дослідження залежностей даних за допомогою лінійного регресійного аналізу

МІНИСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНЕВЕРСИТЕТ

«ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»

Звіт до лабораторної роботи №5

з курсу “Планування експерименту та обробка експериментальних даних”

Виконав:

Студент гр. КІТ-14в

Богачов О. С.

Перевірив:

Черних О. П.

Харків – 2006

Лабораторна робота №5.

Лінійний регресійний аналіз.

Мета:

Дослідження залежностей даних за допомогою лінійного регресійного аналізу.

Хід роботи:

1.  За допомогою процедури “Relate-simple regression” досліджуемо вхідні залежності:

x = { 0,1; 2; 3,5; 4; 6 }, y = {9,5; 21,1; 36,7; 45,7; 99 }

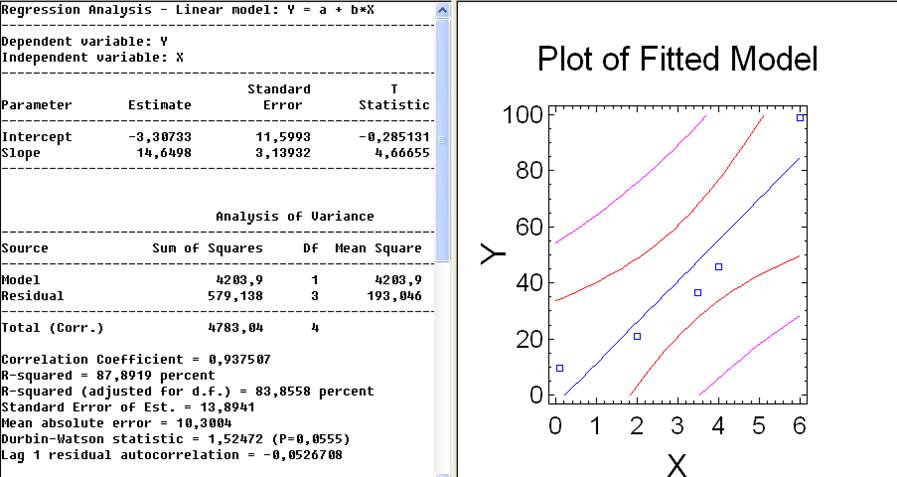
Одержуемо статистичні характеристики:  оцінки параметрів регресії, стандартна помилка, кореляційні коєфіціенти для найкращих 2 моделей.

Regression Analysis - Linear model: Y = a + b*X

Comparison of Alternative Models

--------------------------------------------------

Model                  Correlation       R-Squared

--------------------------------------------------

Exponential                 0,9998          99,95%

Square root-Y               0,9830          96,63%

Double reciprocal           0,9434          89,00%

Linear                      0,9375          87,89%

Multiplicative              0,8996          80,92%

Square root-X               0,8374          70,13%

S-curve                    -0,7904          62,47%

Logarithmic-X               0,7003          49,04%

Reciprocal-X               -0,5515          30,41%

Reciprocal-Y                       <no fit>

Logistic                           <no fit>

Log probit                         <no fit>

--------------------------------------------------

Розрахуємо для найкращої моделі(експонентна)оцінки параметрів регресії, стандартну помилку, кореляційні коефіцієнти.

Проведемо розрахунки для Exponential (Y = exp(a + b*X))

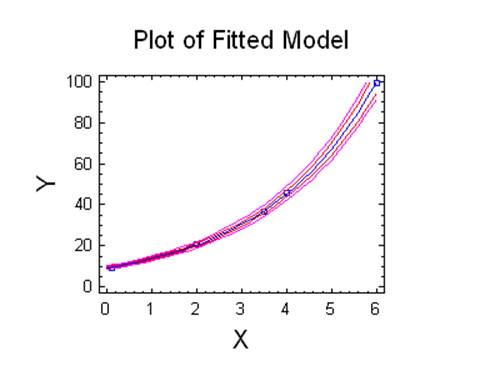
Regression Analysis - Exponential model: Y = exp(a + b*X)

-----------------------------------------------------------------------------

Dependent variable: Y

Independent variable: X

-----------------------------------------------------------------------------

                               Standard          T

Parameter       Estimate         Error       Statistic        P-Value

-----------------------------------------------------------------------------

Intercept        2,22931      0,0182069        122,443         0,0000

Slope           0,395771     0,00492763        80,3166         0,0000

-----------------------------------------------------------------------------

                           Analysis of Variance

-----------------------------------------------------------------------------

Source             Sum of Squares     Df  Mean Square    F-Ratio      P-Value

-----------------------------------------------------------------------------

Model                     3,06816      1      3,06816    6450,76       0,0000

Residual               0,00142688      3  0,000475627

-----------------------------------------------------------------------------

Total (Corr.)             3,06959      4

Correlation Coefficient = 0,999768

R-squared = 99,9535 percent

R-squared (adjusted for d.f.) = 99,938 percent

Standard Error of Est. = 0,0218089

Mean absolute error = 0,015253

Durbin-Watson statistic = 3,17634 (P=0,0018)

Lag 1 residual autocorrelation = -0,723828

Exponential model: Y = exp(a + b*X)

Модель зворотня відносно Y – це нелінійна модель, тому її треба привести до лінійного вигляду за рахунок математичних перетворень.

Y=ln y;

X	X	0,1	2	3.5	4	8
Y	ln y	2.25	3.05	3.6	3.82	4.6

Розрахуємо задані характеристики. Для цього побудуємо матрицю плану:

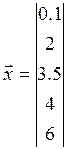
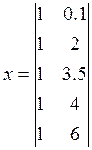              Побудуємо вектор вихідних значень: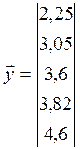

Знаходимо вектор коефіцієнтів, користуючись методом найменших квадратів (середньоквадратичне відхилення повинно прямувати до мінімуму):

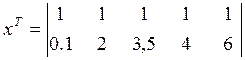
Знаходимо інформаційну матрицю:

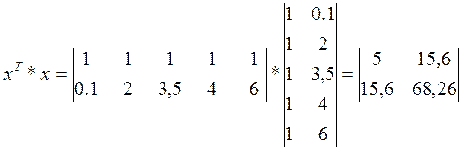
Знаходимо дисперсійну матрицю:

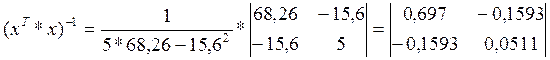
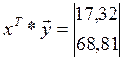
Знаходимо вектор коефіцієнтів:

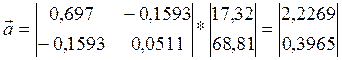
Знаходимо стандартну помилку для кожної оцінки та кореляційні коефіцієнти, записавши вектор помилок:

 

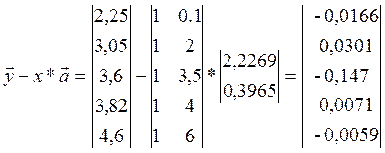
Знаходимо дисперсію:

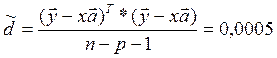
Знаходимо довірюючі інтервали:

                                                                  

;                                                                

Знайдемо коефіціент кореляціі для експоненціальної моделі відносно У

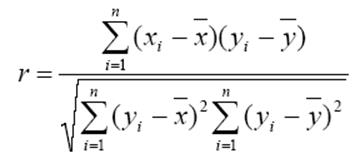
r=0,9998           

Висновки: в результаті дослідження послідовності було визначено тип залежності.