





МІНИСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНЕВЕРСИТЕТ
«ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»
Звіт до лабораторної роботи №4
з курсу “Планування експерименту та обробка експериментальних даних”
Виконав:
Студент гр. КІТ-14в
Богачов О. С.
Перевірив:
Черних О. П.
Харків – 2006
Кореляційний аналіз.
Мета:
Хід роботи:
У роботі треба визначити наявність статистичного зв’язку між ординальними (порядковими) змінними.
|
X |
5 |
7 |
4 |
6 |
10 |
8 |
2 |
3 |
9 |
1 |
|
Y |
4 |
3 |
5 |
10 |
8 |
2 |
9 |
7 |
6 |
1 |
Перейдемо до Describe > Numeric Data > Multiple-Variable Analysis та виберемо 2 змінні.
У Tabular Options оберемо пункти Corellations та Rank Correlations.
|
|
|
Коефіцієнт Пірсона:
|
|
= 0,10303 |
Перевіримо значущість коефіцієнта.
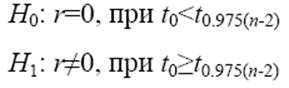
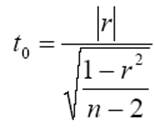
t0 = 0.29297
t0,975(n-2)= 2,30601
Коефіцієнт Спірмена:
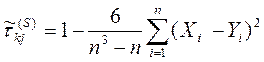 =
=![]()
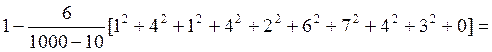
= 0,10303
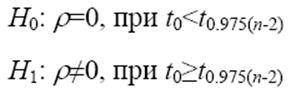
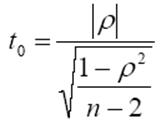
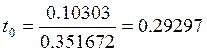
t0=0.29297
t0,975(n-2)= 2,30601
КоефіцієнтКендела:
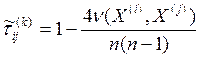
Спочатку підрахуємо кількість обмінів.
Впорядкуємо послідовність:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
9 |
7 |
5 |
4 |
10 |
3 |
2 |
6 |
8 |
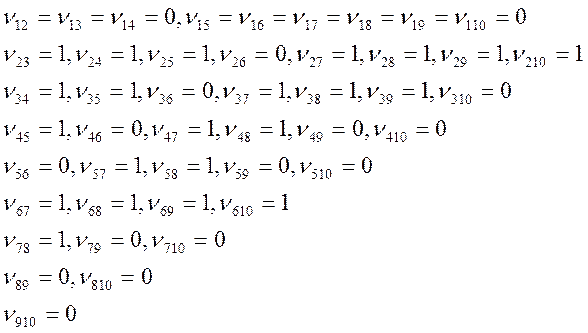
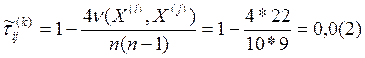

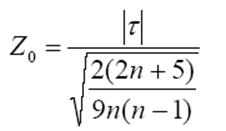
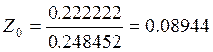
Z0=0,08944
Z0,975= 1,95997 (нормальне розподілення)
Перевіримо коефіцієнти кореляції для послідовності з повторюваними значеннями.
|
X |
3 |
3 |
3 |
4 |
5 |
1 |
5 |
2 |
6 |
7 |
|
Y |
3 |
4 |
1 |
1 |
2 |
4 |
2 |
3 |
4 |
5 |



Коефіцієнт кореляції Пірсона:
![]() ,
, ![]()
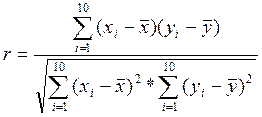 =
=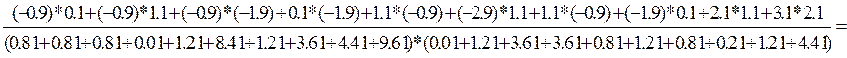
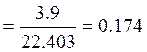
Перевірка значущості коефіцієнта Пірсона:
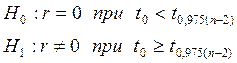
![]()
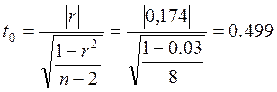
Коефіцієнт кореляції Спірмена:
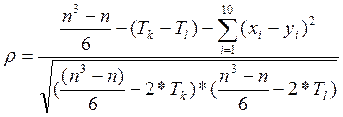 ,
, 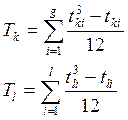
Де 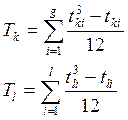 ,
, ![]() — кількість значень в
кожній з q груп однакових значень послідовності k та l однакових значень
послідовності p.
— кількість значень в
кожній з q груп однакових значень послідовності k та l однакових значень
послідовності p.
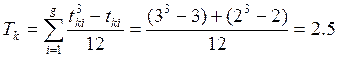
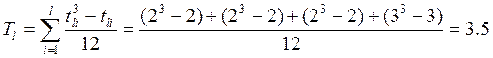
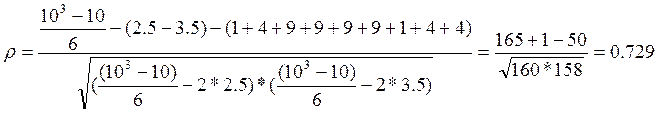
Перевірка значущості коефіцієнту кореляції Спірмена:
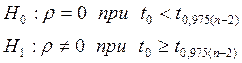
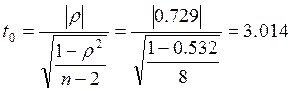
Коефіцієнт кореляції Кендала:
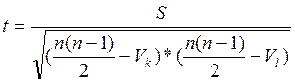
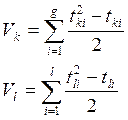
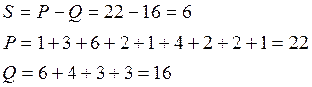
|
1 |
2 |
3 |
3 |
3 |
4 |
5 |
5 |
6 |
7 |
|
1 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
4 |
5 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
2 |
4 |
4 |
4 |
7 |
7 |
7 |
9,5 |
9,5 |
|
1.5 |
1.5 |
3 |
2 |
5.5 |
5.5 |
5 |
8.5 |
8.5 |
6 |
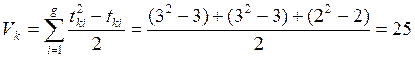
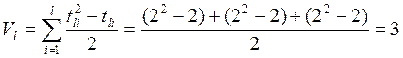
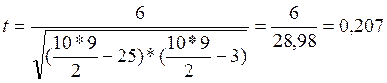
Перевірка значущості коефіцієнта кореляції:
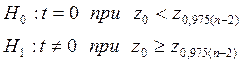 ,
,
z0,975=1,96
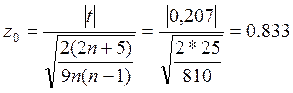
Висновок: Виконавши лабораторну роботу, отримали практичні навички по встановленню статистичного зв’язку між сукупностями даних за допомогою коефіцієнтів кореляції Спірмена, Кендала, Пірсона.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.