




МІНИСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНЕВЕРСИТЕТ
«ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»
Звіт до лабораторної роботи №1
з курсу “Планування експерименту а обробка експериментальних даних”
Виконав:
Студент гр. КІТ-14в
Богачов О. С.
Перевірив:
Черних О. П.
Харків – 2006
Лабораторна робота №1
Тема: Визначення статичних характеристик даних
Мета: Ознайомитися з пакетом Statgraphics 5, розрахувати статичні характеристики вибірки, ознайомитися з основними видами розподілу даних.
Хід виконання роботи:
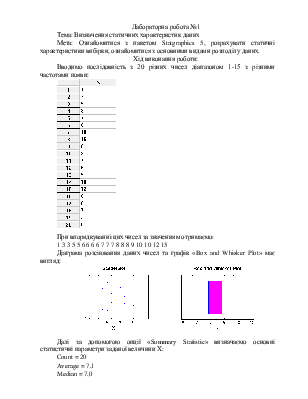
Вводимо послідовність з 20 різних чисел діапазоном 1-15 з різними частотами появи:
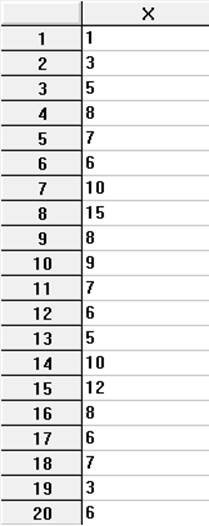
При впорядкуваннi цих чисел за значенням отримаємо:
1 3 3 5 5 6 6 6 6 7 7 7 8 8 8 9 10 10 12 15
Діаграма розсіювання даних чисел та графік «Box and Whisker Plot» має вигляд:
|
|
|
Далі за допомогою опції «Summary Statistic» визначаємо основні статистичні параметри заданої величини Х:
Count = 20
Average = 7,1
Median = 7,0
Mode = 6,0
Geometric mean = 6,25091
Variance = 10,2
Standard deviation = 3,19374
Standard error = 0,714143
Minimum = 1,0
Maximum = 15,0
Range = 14,0
Lower quartile = 5,5
Upper quartile = 8,5
Interquartile range = 3,0
Skewness = 0,502358
Stnd. skewness = 0,917176
Kurtosis = 1,05902
Stnd. kurtosis = 0,966752
Coeff. of variation = 44,9823%
Sum = 142,0
Mediana — медіана являє собою середнє значення впорядкованого у порядку зростання ряду чисел.
Mode — мода це значення, яке найчастіше зустрічається.
Визначимо основні аналітичні розрахунки заданих статичних характеристик і порівняємо їх з розрахунками, що отримані за допомогою пакету Statgraphics 5.
Розрахунки:
Кількість: С=20
Математичне очікування:
M= 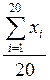 =
=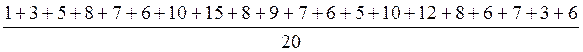 =7,1;
=7,1;
Медіана: МН=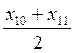 =7
=7
Мода:МД=6
Середнє геометричне:
СГ=![]() = 6,25091
= 6,25091
Дисперсія:
D=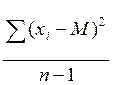 =
=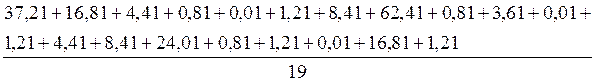 =10,2
=10,2
Стандартне відхилення:
δ=![]() =
=![]() =3,19374
=3,19374
Стандартна помилка:
СП=![]() =
=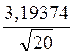 =0,714143
=0,714143
Мінімум:
min=1
Максимум:
max=15
Діапазон:
D=15-1=14
Нижній квартиль:
i=ceil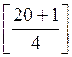 =6
j=ceil
=6
j=ceil![]() =5
=5
LQ=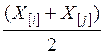 =
=![]() =5,5
=5,5
Верхній квартиль:
i=ceil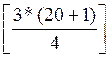 =16
j=ceil
=16
j=ceil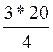 =15
=15
UQ=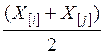 =
=![]() =8,5
=8,5
Межквартильний діапазон:
MD=UQ-LQ=8,5-5,5=3;
Коефіцієнт асиметрії:
КА=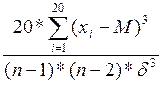 =
=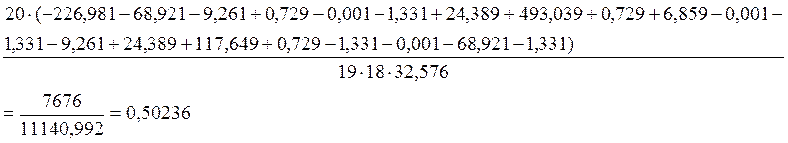
Стандартизований коефіцієнт асиметрії:
СКА=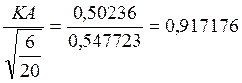
Коефіцієнт ексцесу:
КЕ=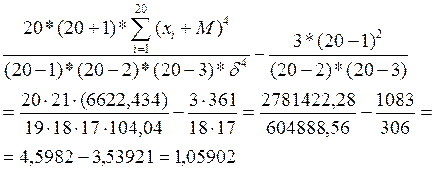
Стандартизований коефіцієнт ексцесу:
СКЕ=![]() =
=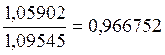
Коефіцієнт варіації:
КВ=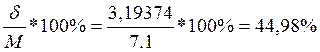
Сума:
SM= ![]() = 142
= 142
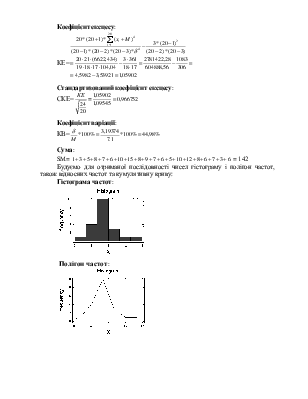
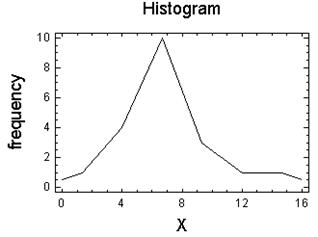
Будуємо для отриманої послідовності чисел гістограму і полігон частот, також відносних частот та кумулятивну криву:
Гiстограма частот:
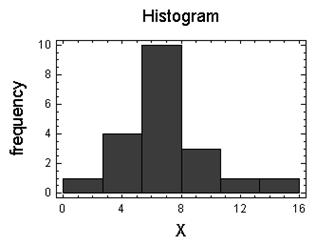
Полiгон частот:
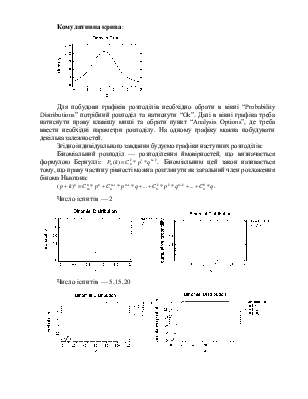
Комулятивна крива:
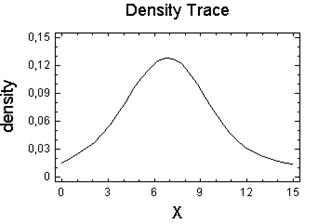
Для побудови графіків розподілів необхідно обрати в вікні “Probability Distributions” потрібний розподіл та натиснути “Ok”. Далі в вікні графіка треба натиснути праву клавішу миші та обрати пункт “Analysis Options”, де треба ввести необхідні параметри розподілу. На одному графіку можна побудувати декілька залежностей.
Згідно індивідуального завдання будуємо графіки наступних розподілів:
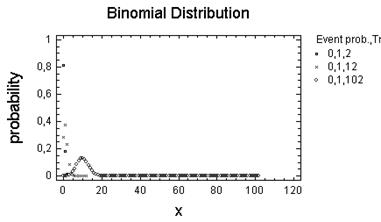
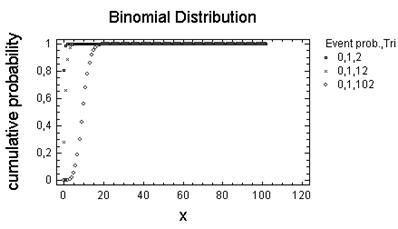
Біноміальний розподіл — розподілення ймовірностей, що визначається
формулою Бернуллі: ![]() . Біноміальним цей закон називається тому, що
праву частину рівності можна розглянути як загальний член розложення бінома
Ньютона:
. Біноміальним цей закон називається тому, що
праву частину рівності можна розглянути як загальний член розложення бінома
Ньютона:
![]() .
.
Число іспитів — 2
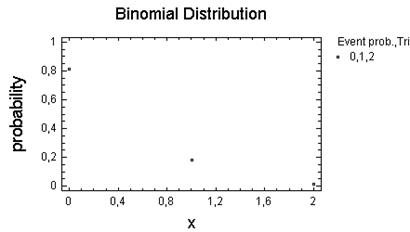
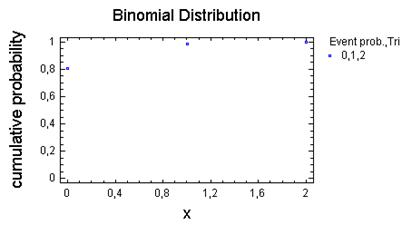
Число іспитів — 5,15,20
Нормальний розподіл — розподіл ймовірностей неперервної випадкової величини, яке описується диференціальною функцією.
ƒ(x)=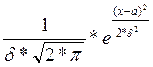
Параметри: (мат.очікування, середньоквадратичне відхилення)
(0,1),(0.6,1),(0,1.8),(0.6,1.8)
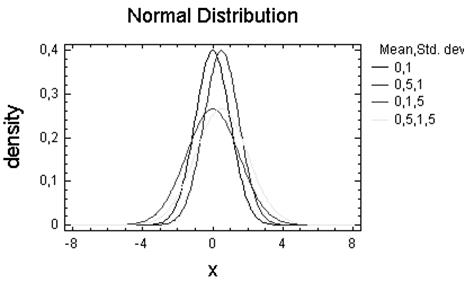
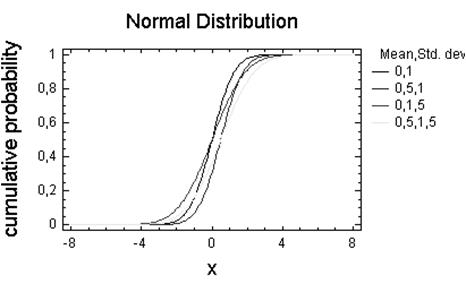
Висновок: Змінення величини математичного очікування не змінює форми нормальної кривої, а приводить лише до її зсуву вздовж осі Х (вправо, якщо математичне очікування збільшується і вліво-, якщо зменшується).
ХI-Квадрат
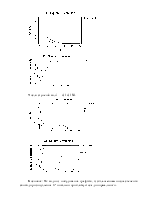
Число ступенiв волi — 2, 4.
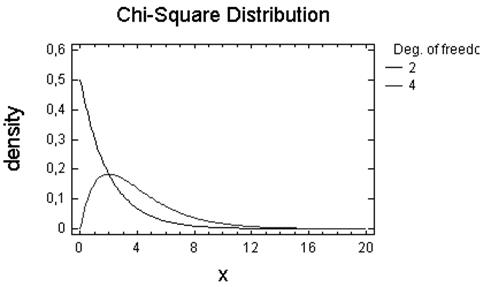
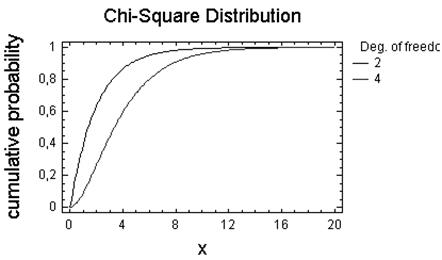
Число ступенiв волi — 4, 14, 104.
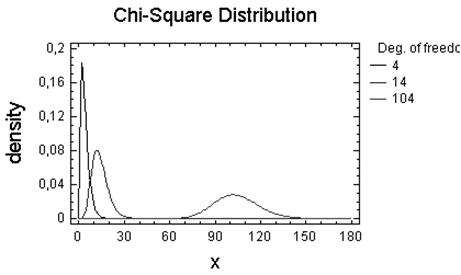
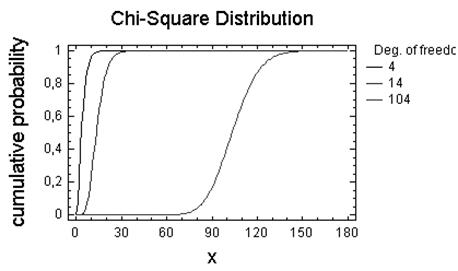
Висновок: Як видно з побудованих графіків, із збільшенням числа степенів
свободи розподілення ![]() повільно приближується до
нормального.
повільно приближується до
нормального.
Розподілення Стьюдента:
Нехай Z-нормальна випадкова величина, при чому M(Z)=0,
![]() , а V- незалежна від Z
велечина, яка розподілена по
закону
, а V- незалежна від Z
велечина, яка розподілена по
закону ![]() з k степенями свободи. Тоді величина T=
з k степенями свободи. Тоді величина T=![]() має
розподілення, яке називають t-розподілення, або розподіленням Стьюдента з k
степенями свободи.
має
розподілення, яке називають t-розподілення, або розподіленням Стьюдента з k
степенями свободи.
Параметри: 6, 24, 106,3000.
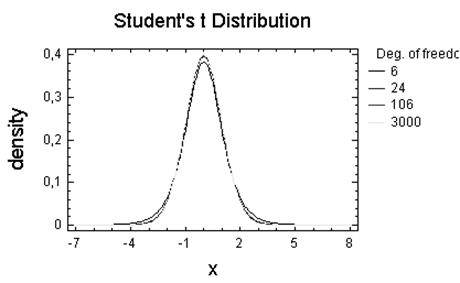
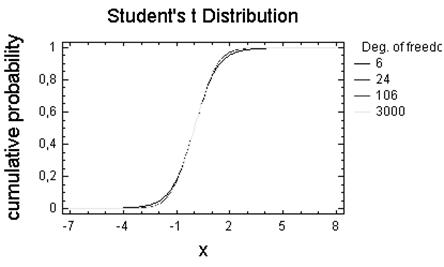
Висновок: Як видно з побудованих графіків, зі збільшенням числа степенів свободи розподілення Стьюдента швидко приближується до нормального.
Розподілення Фішера:
Якщо U і V — незалежні випадкові величини, що розподілені по
закону ![]() зі степенями свободи
зі степенями свободи ![]() та
та ![]() , то величина
, то величина 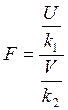 має розподілення,
яке називають розподіленням F Фішера зі степенями свободи k1 i k2.
має розподілення,
яке називають розподіленням F Фішера зі степенями свободи k1 i k2.
Параметри: 75; 15.
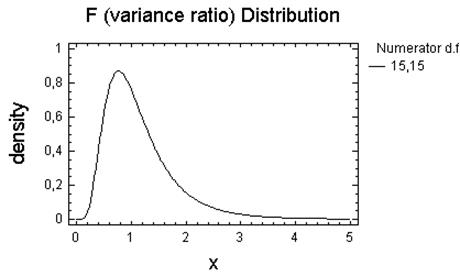
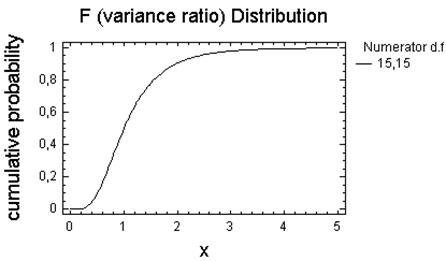
Параметри: (75, 15), (15,75).
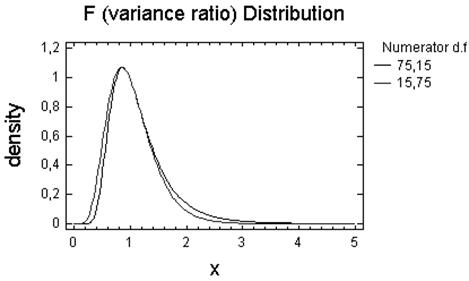
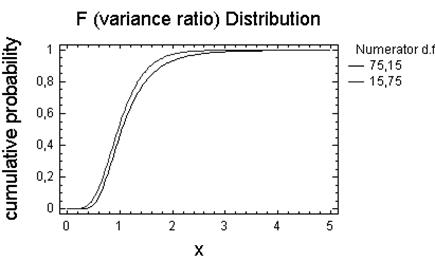
Висновок: З побудованих графiкiв видно, що при збiльшеннi степенi свободи k2 розподiлення Фiшера повыльно наближується донормального розподiлення.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.