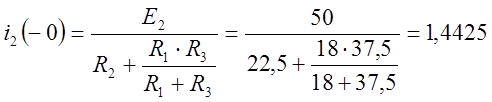 (А).
(А).
На основании законов коммутации имеем:
![]() . (1)
. (1)
1.2. После первой коммутации (ключ К33 разомкнулся) электрическая цепь принимает вид, показанный на рисунке 7.
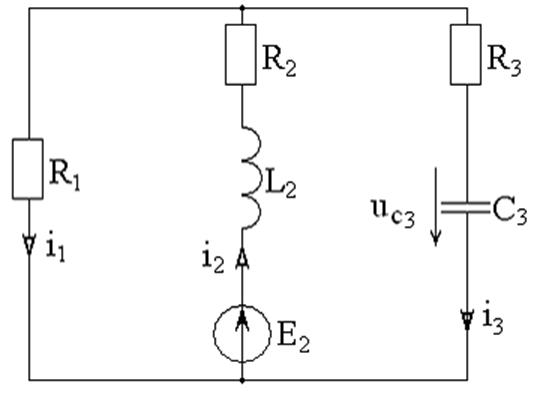
Рисунок 7 – Схема цепи после первой коммутации
Режим работы цепи после первой коммутации опишется уравнениями по законам Кирхгофа:
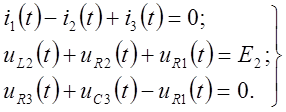 (2)
(2)
Или с учётом компонентных соотношений для элементов:
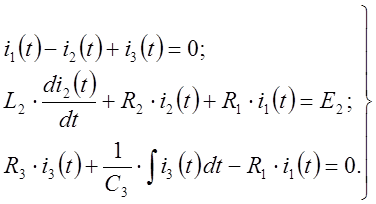 (2/ )
(2/ )
1.3. Для цепи после коммутации (рисунок 7) получим характеристическое уравнение. Для этого составим входное операторное сопротивление цепи относительно любой ветви (например, для второй ветви) и приравняем его нулю:
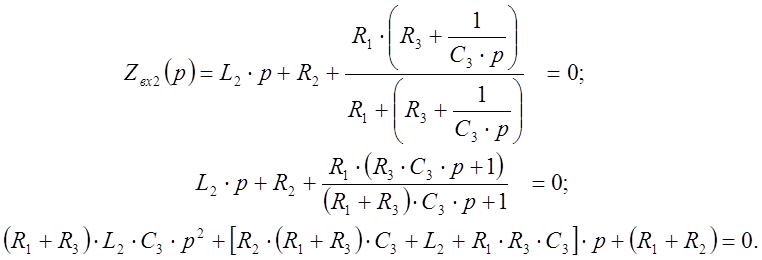
После подстановки числовых значений параметров элементов цепи получаем характеристическое уравнение цепи:
![]() ;
;
или
![]() .
.
1.4. Находим корни характеристического уравнения.
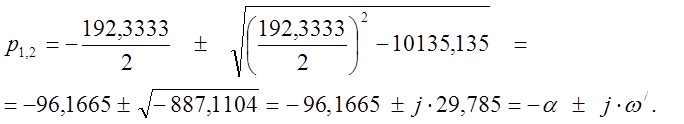 (3)
(3)
Корни
комплексные сопряжённыё, т.е. переходный процесс после первой коммутации
периодический. Здесь: ![]() – коэффициент затухания,
– коэффициент затухания, 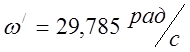 – частота затухающих колебаний.
– частота затухающих колебаний.
1.5. Рассматриваем установившийся режим после коммутации и находим принуждённые (установившиеся) составляющие токов ветвей и напряжения ёмкости. Так как в этом режиме токи и напряжения постоянные, то напряжение индуктивности и ток ветви с ёмкостью равны нулю (рисунок 8).
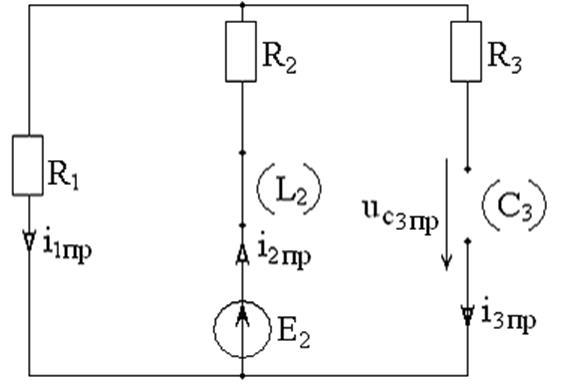
Рисунок 8 – Установившийся режим цепи после первой коммутации
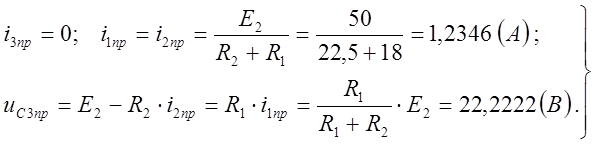 (4)
(4)
1.6. Находим зависимые начальные условия (граничные условия в момент коммутации). Для этого запишем уравнения для цепи после коммутации (2, 2/) для момента коммутации t = 0:
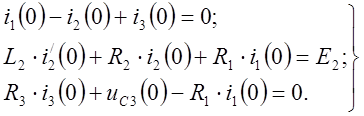
Решив полученную систему уравнений с учётом известных независимых начальных условий (1), найдём зависимые начальные условия:
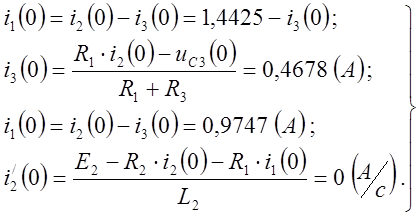 (5)
(5)
Для нахождения начальных значений производных токов продифференцируем систему уравнений для цепи (2/) и запишем полученные уравнения для момента коммутации (t = 0):
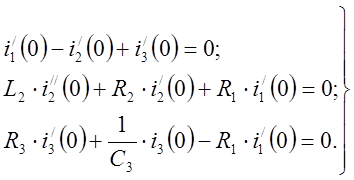
Решив полученную систему уравнений с учётом известных начальных условий (1, 5), найдём начальные значения первых производных токов:
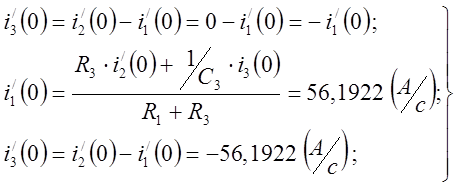 (6)
(6)
1.7. Определим закон изменения искомого тока после первой коммутации.
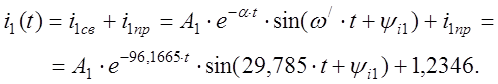
Для определения постоянных интегрирования имеем систему уравнений (с учётом найденных начальных значений):
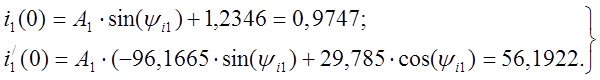
Решение системы уравнений:
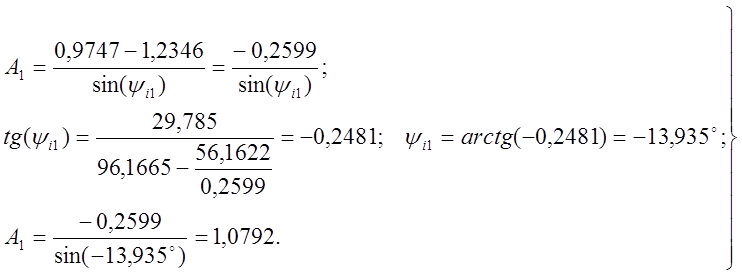
Закон изменения искомого тока после первой коммутации:
![]() . (7)
. (7)
1.8. Определим закон изменения тока в ветви с индуктивностью после первой коммутации.
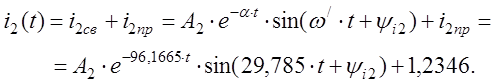
Для определения постоянных интегрирования имеем систему уравнений:
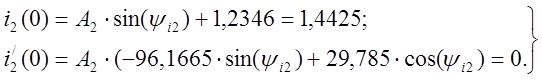
Решение системы уравнений:
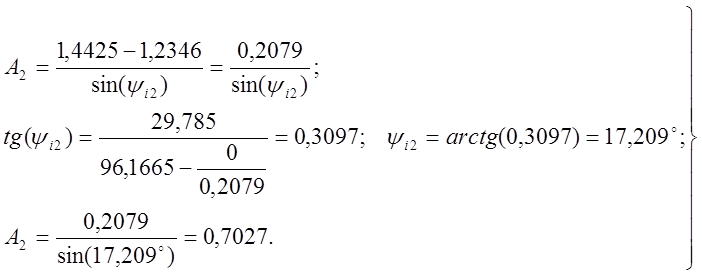
Закон изменения тока в индуктивности после первой коммутации:
![]() . (8)
. (8)
1.9. Определим закон изменения напряжения ёмкости после первой коммутации.
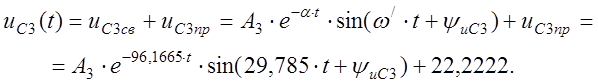
Для определения постоянных интегрирования имеем систему уравнений (с учётом найденных начальных значений):
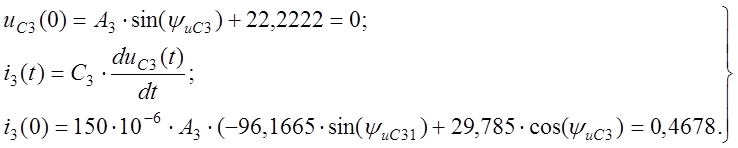
Решение системы уравнений:
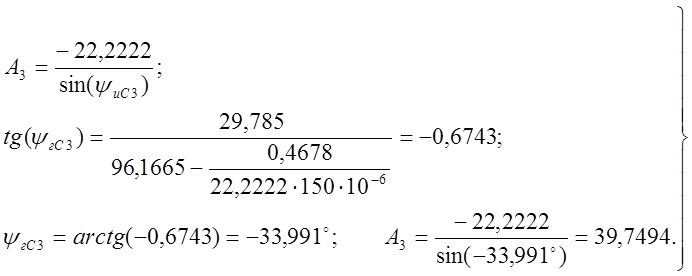
Закон изменения напряжения ёмкости после первой коммутации:
![]() . (9)
. (9)
2. РАСЧЁТ ВТОРОЙ КОММУТАЦИИ (ключ К21 замыкается).
2.1. Вторая
коммутация происходит, когда после первой коммутации процесс ещё не
установился. Независимыми начальными условиями для второй коммутации будут: ток
ветви с индуктивностью и напряжение ёмкости к моменту второй коммутации.
Срабатывание второго ключа происходит при ![]() . Так
как после первой коммутации переходный процесс – периодический
(колебательный), то момент второй коммутации определится:
. Так
как после первой коммутации переходный процесс – периодический
(колебательный), то момент второй коммутации определится:
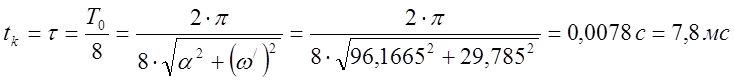 .
.
Ток ветви с индуктивностью и напряжение ёмкости к моменту второй коммутации будут равны:
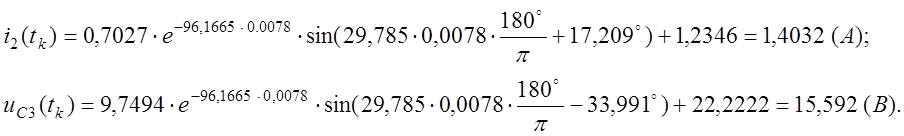
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.