







Федеральное агентство по образованию
Государственное образовательное
учреждение
высшего профессионального образования
“Сибирский государственный индустриальный университет”
Кафедра АЭП и ПЭ
Отчет по лабораторной работе № 4
Основные способы коррекции линейных непрерывных САУ
Вариант 1
Выполнил: студент гр.АЭП-042
Афанасьев Н.Ю.
Ручкин А.С.
Принял: к.т.н, доцент
Богдановская Т.В.
Новокузнецк, 2007 г.
Цель: изучить и освоить основные способы определения количественных характеристик устройств, обеспечивающих коррекцию динамических свойств проектируемых систем управления в рамках наиболее часто используемых в практике структур САУ.
1.) Синтез последовательного КУ из условия настройки на модульный оптиум.
По данным варианта записываем передаточные функции объекта управления и устройства обратной связи:
>> Woy=tf(7,[0.007 0.37 1])
Transfer function:
7
----------------------
0.007 s^2 + 0.37 s + 1
>> Woc=tf(1,[0.015 1])
Transfer function:
1
-----------
0.015 s + 1
Передаточная функция неизменяемой части и желаемая передаточная функция разомкнутой системы запишутся:
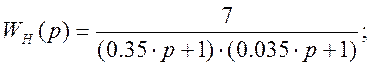
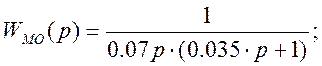
![]() -
суммарная постоянная времени системы;
-
суммарная постоянная времени системы;
Определяем ПФ регулятора:
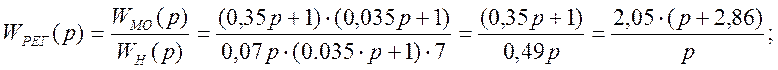
Корректирующее устройство представляет собой ПИ – регулятор с коэффициентом k =2,05 и постоянной времени Tрег = 1с.
Передаточная функция оптимизированного контура имеет вид:
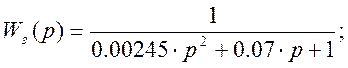
Построение ЛАЧХ для Wн(p), Wмо(p), Wрег(p), Wз(p):
>> Wn=tf(7,[0.01225 0.385 1])
Transfer function:
7
-------------------------
0.01225 s^2 + 0.385 s + 1
>> Wmo=tf(1,[0.00245 0.07 0])
Transfer function:
1
--------------------
0.00245 s^2 + 0.07 s
>> Wreg=zpk(-2.86,[0],2.05)
Zero/pole/gain:
2.05 (s+2.86)
-------------
S
>> Wz=tf(1,[0.00245 0.07 1])
Transfer function:
1
------------------------
0.00245 s^2 + 0.07 s + 1
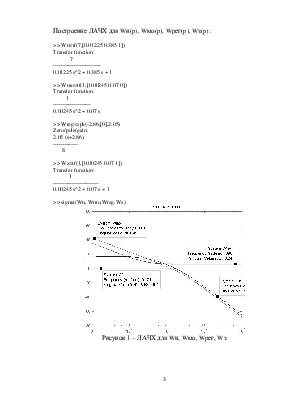
>> sigma(Wn, Wmo,Wreg,Wz)
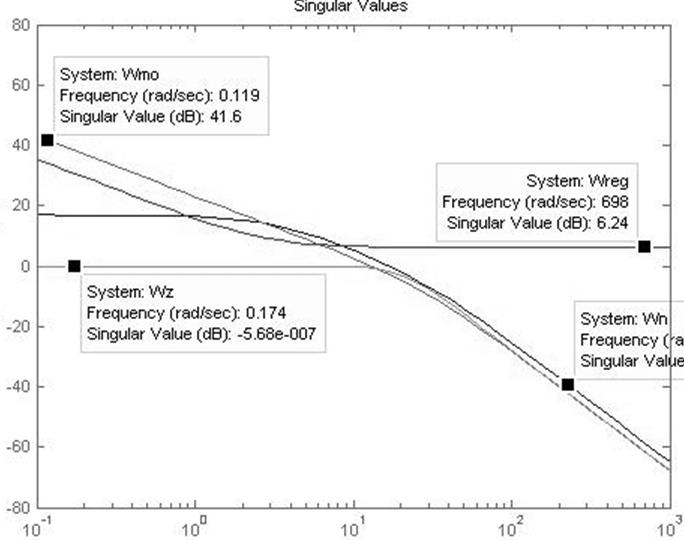
Рисунок 1 – ЛАЧХ для Wн, Wмо, Wрег, Wз
Запишем действительную ПФ замкнутой с-мы:
>> Wdd=tf([2050 136673.5],[1 116.67 3333.877 136709.84])
Transfer function:
2050 s + 1.367e005
------------------------------------
s^3 + 116.7 s^2 + 3334 s + 1.367e005
Построение переходной характеристики по передаточной функции Wз(p):
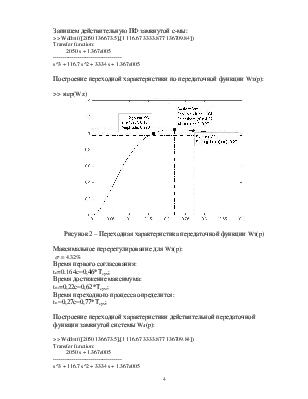
>> step(Wz)
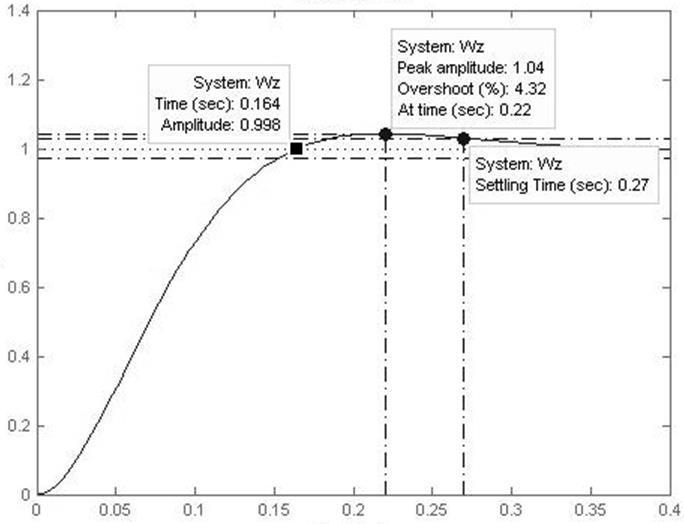
Рисунок 2 – Переходная характеристика передаточной функции Wз(p)
Максимальное перерегулирование для Wз(p):
![]()
Время первого согласования:
tc=0.164c=0,46*Тсум;
Время достижение максимума:
tm=0,22с=0,62*Тсум;
Время переходного процесса определится:
tп=0,27с=0,77*Тсум;
Построение переходной характеристики действительной передаточной функции замкнутой системы Wd(p):
>> Wdd=tf([2050 136673.5],[1 116.67 3333.877 136709.84])
Transfer function:
2050 s + 1.367e005
------------------------------------
s^3 + 116.7 s^2 + 3334 s + 1.367e005
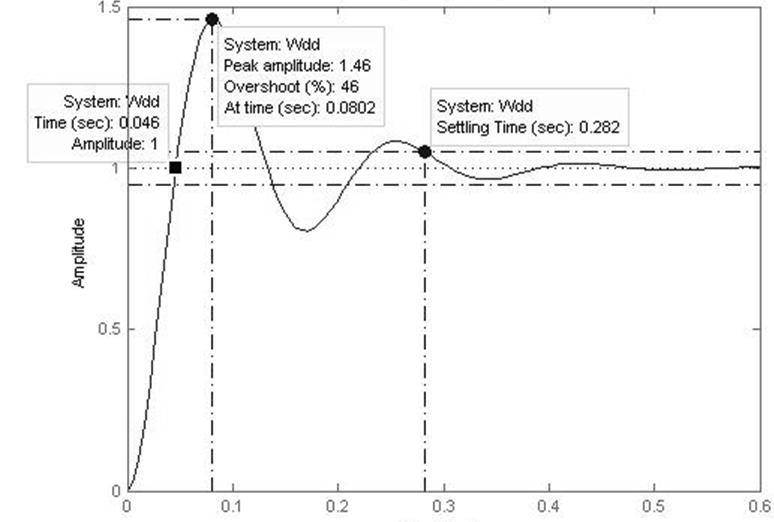
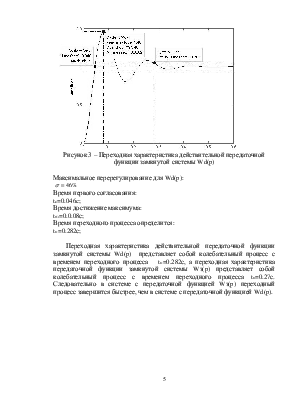
Рисунок 3 – Переходная характеристика действительной передаточной функции замкнутой системы Wd(p)
Максимальное перерегулирование для Wd(p):
![]()
Время первого согласования:
tc=0.046c;
Время достижение максимума:
tm=0.0.08с;
Время переходного процесса определится:
tп=0.282с;
Переходная характеристика действительной передаточной функции замкнутой системы Wd(p) представляет собой колебательный процесс с временем переходного процесса tп=0.282с, а переходная характеристика передаточной функции замкнутой системы Wз(p) представляет собой колебательный процесс с временем переходного процесса tп=0.27с. Следовательно в системе с передаточной функцией Wз(p) переходный процесс завершится быстрее, чем в системе с передаточной функцией Wd(p).
2.) Синтез последовательного КУ из условия на симметричный оптимум.
Передаточные функции объекта управления и устройства обратной связи:
>> Woy=tf(7,[0.02 1 0])
Transfer function:
7
------------
0.02 s^2 + s
>> Woc=tf(1,[0.015 1])
Transfer function:
1
-----------
0.015 s + 1
ПФ неизменяемой части:
>> Wn=tf(7,[0.035 1 0])
Transfer function:
7
-------------
0.035 s^2 + s
Желаемая ПФ разомкнутой системы:
>> Wсо=tf([0.14 1],[0.000343 0.0098 0 0])
Transfer function:
0.14 s + 1
-------------------------
0.000343 s^3 + 0.0098 s^2
Определяем ПФ регулятора:
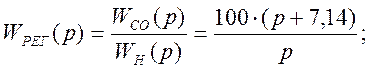
Корректирующее устройство представляет собой ПИ – регулятор с коэффициентом k =100 и постоянной времени Tрег = 1с.
Передаточная функция оптимизированного контура имеет вид:
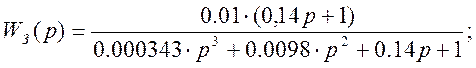
>> sigma(Wn, Wco,Wreg,Wz)
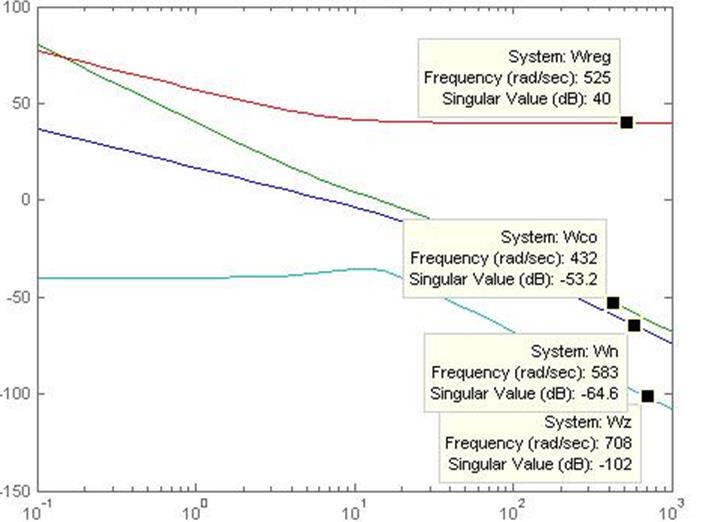
Рисунок 4 – ЛАЧХ для Wн(p), Wсо(p), Wрег(p), Wз(p)
Построение переходной характеристики по передаточной функции Wз(p):
>> step(Wz)
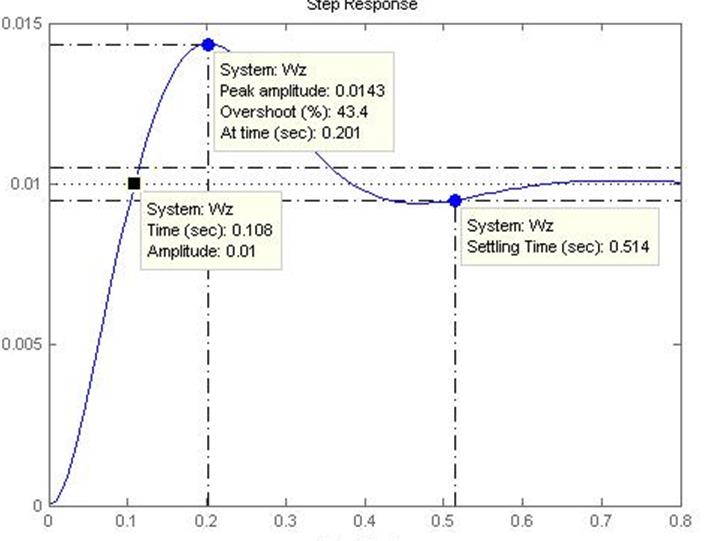
Рисунок 5 – Переходная характеристика передаточной функции Wз(p)
Максимальное перерегулирование для Wз(p):
![]()
Время первого согласования:
tc=0.01c;
Время достижение максимума:
tm=0.201с;
Время переходного процесса определится:
tп=0.514c;
Построение переходной характеристики действительной передаточной функции замкнутой системы Wd(p):
>> Wd=tf([0.0049 0.14 0.035 1],[0.00000294 0.000343 0.0098 0.14 1])
Transfer function:
0.0049 s^3 + 0.14 s^2 + 0.035 s + 1
------------------------------------------------------
2.94e-006 s^4 + 0.000343 s^3 + 0.0098 s^2 + 0.14 s + 1
>> step(Wd)
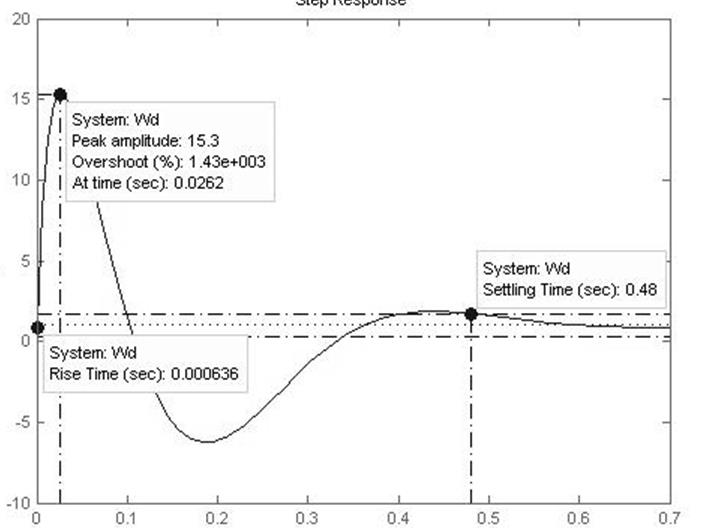
Рисунок 6 – Переходная характеристика для передаточной функции Wd(p)
Максимальное перерегулирование для Wd(p):
![]()
Время первого согласования:
tc=0.000636c;
Время достижение максимума:
tm=0.0262с;
Время переходного процесса определится:
tп=0,48с
Переходная характеристика действительной передаточной функции замкнутой системы Wd(p) представляет собой колебательный процесс с временем переходного процесса tп=0,48с, а переходная характеристика передаточной функции замкнутой системы Wз(p) представляет собой колебательный процесс с временем переходного процесса tп=0,514с. Следовательно в системе с передаточной функцией Wd(p) переходный процесс завершится быстрее, чем в системе с передаточной функцией Wз(p).
3.) Синтез параллельного КУ (внутренней ОС).
Передаточная функция неизменяемой части определится:
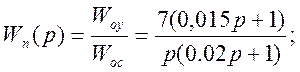
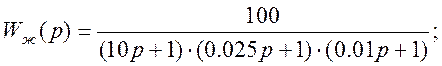
Передаточная функция корректирующего устройства:
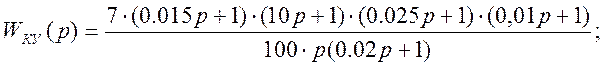
ПФ охваченных звеньев:
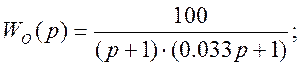
Передаточная функция разомкнутого внутреннего контура и проверка контура на устойчивость:
![]()
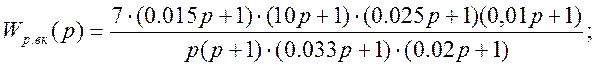
Проверка контура на устойчивость:
>> W=zpk([-66.6 -0.1 -40 -100],[-1 -30.3 -50 0],0.4)
Zero/pole/gain:
0.4 (s+66.6) (s+100) (s+40) (s+0.1)
-----------------------------------
s (s+1) (s+30.3) (s+50)
Для проверки контура на устойчивость строим корневой годограф и находим критические коэффициенты k
>> rlocus(W)
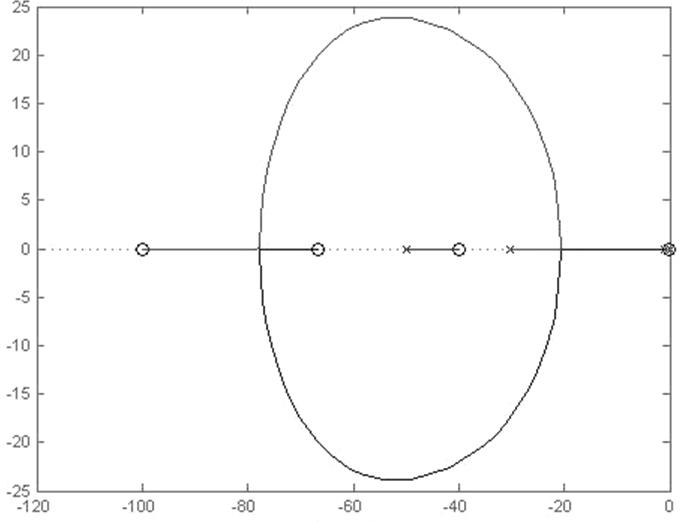
Рисунок 7 – Корневой годограф
При любых k
Передаточная функция замкнутого внутреннего контура Wвк(p):
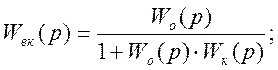
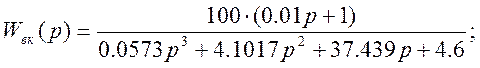
С учётом поправки желаемая передаточная функция системы имеет вид:
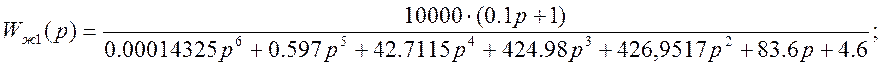
Построение ЛАЧХ для Wж(p), W(p),Wн(p), Wвк(p):
>> Wg=tf(100,[0.0025 10.25025 10.035 1])
Transfer function:
100
------------------------------------
0.0025 s^3 + 10.25 s^2 + 10.04 s + 1
>> Wg1=tf([1000 10000],[0.00014325 0.597 42.7115 424.98 426.9517 83.6 4.6])
Transfer function:
1000 s + 10000
------------------------------------------------------------------------
0.0001433 s^6 + 0.597 s^5 + 42.71 s^4 + 425 s^3 + 427 s^2 + 83.6 s + 4.6
>> Wn=tf([0.216 3.6],[0.001 0.11 1])
Transfer function:
0.216 s + 3.6
----------------------
0.001 s^2 + 0.11 s + 1
>> Wbk=tf([10 100],[0.0573 4.1017 37.439 4.6])
Transfer function:
10 s + 100
--------------------------------------
0.0573 s^3 + 4.102 s^2 + 37.44 s + 4.6
>> sigma(Wg,Wg1,Wn,Wbk)
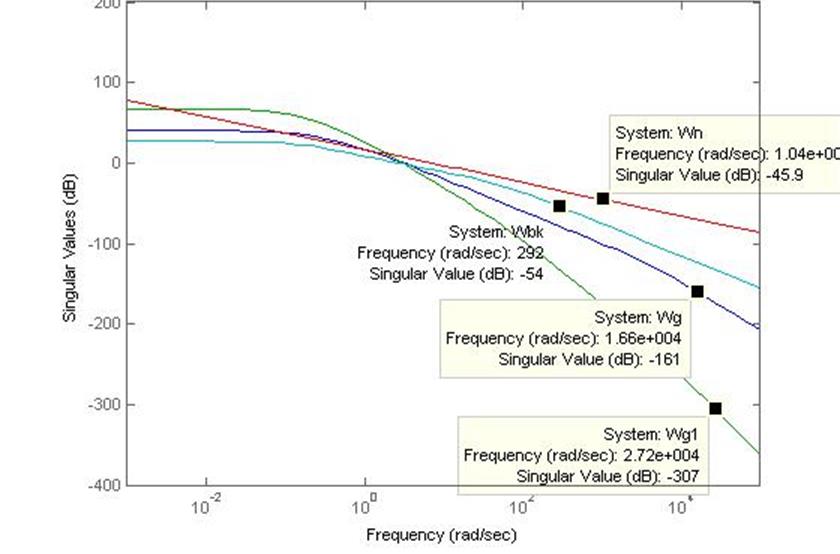
Рисунок 8 – ЛАЧХ передаточных функций: Wж(p), Wж1(p), Wн(p), Wвк(p)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.