Освоение методов анализа и синтеза систем автоматического управления, страница 4

Рисунок 2.6. Структурная схема САР с возмущением приведенным ко входу.

В качестве  и  возьмем соответственно их дискретные формы – уравнения (2.20) и (2.22). Графическое представление перходного процесса представлено на рис. 2.7.

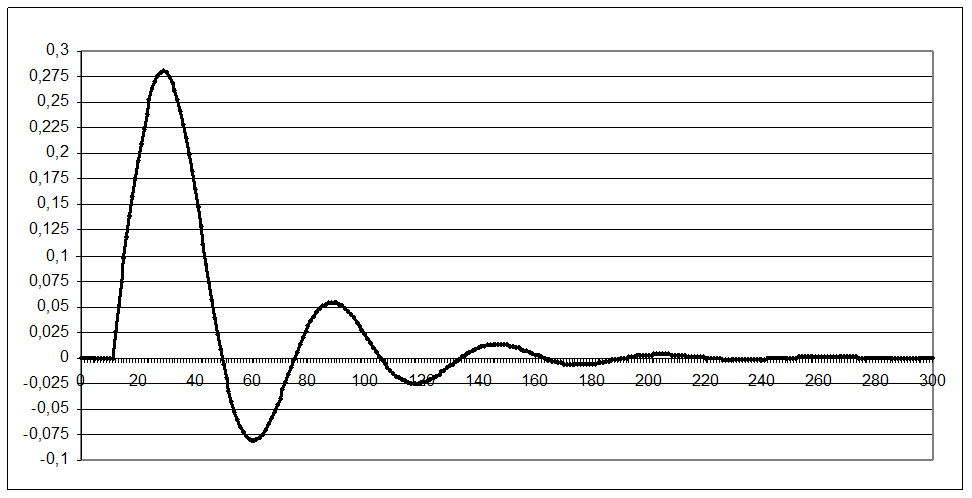Рисунок 2.7. Переходный процесс САР по возмущению.

Оценим качество переходного процесса. Для этого применим критерии рассмотренные выше.

1)  Максимальное динамическое отклонение.

2)  Динамический коэффициент регулирования.

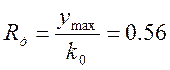
3)  Время регулирования.

4)  Показатель перерегулирования.

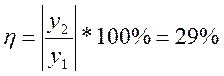
5)  Интегральный квадратичный критерий.

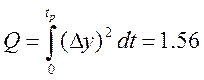
2.4 Анализ влияния вариации коэффициентов модели объекта на показатели качества регулирования.

Проанализируем влияние вариации коэффициентов модели ОУ на показатели качества переходного процесса, при этом настроим регулятор в соответствии с рекомендациями данными в [4, 40].

Для анализа возьмем 2 показателя качества регулирования: интегральный квадратичный критерий  и время регулирования . Результаты численных исследований для САР с типовым законом регулирования при раздельном изменении параметров представлены на рис. 2.8-2.10. Система управления с ПИ – регулятором относительно нечувствительна к изменениям постоянной времени  и достаточно сильно чувствует вариации времени запаздывания и коэффициента передачи  объекта.

 

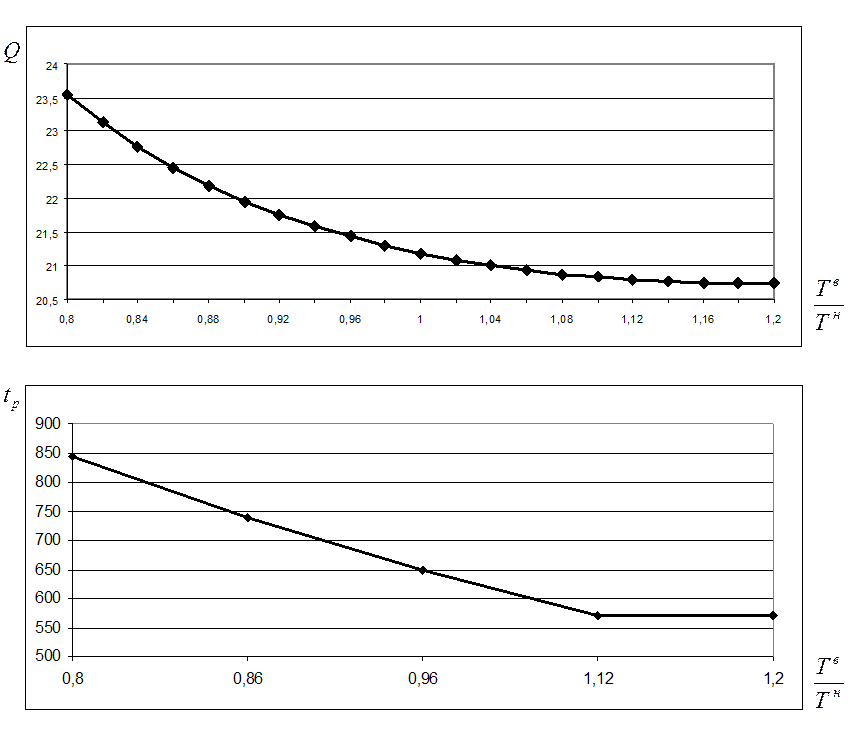
Рисунок 2.8. Влияние изменений постоянной времени  модели ОУ на показатели качества регулирования.

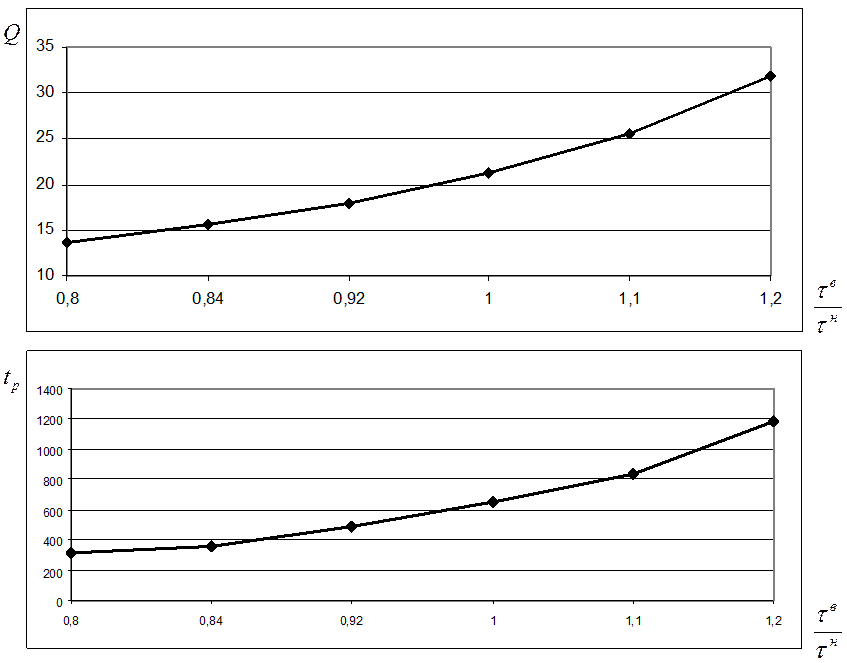
Рисунок 2.9. Влияние изменений времени запаздывания модели ОУ на показатели качества регулирования.

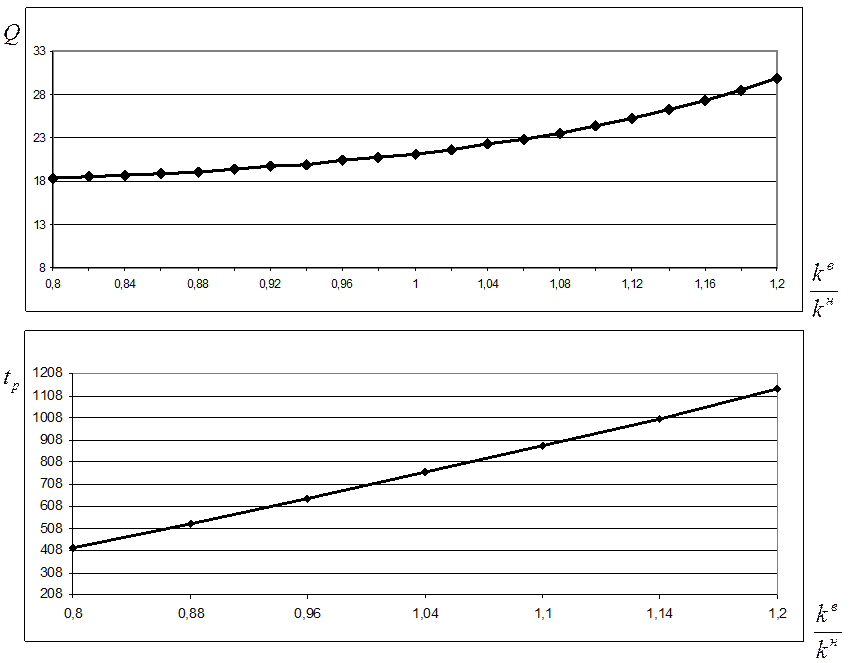
Рисунок 2.10. Влияние изменений коэффициента передачи модели ОУ на показатели качества регулирования.

3. Синтез и анализ прогнозирующей САР.

Дано:

a)  Модель ОУ (операторное выражение 1.3).

b)  Тип объекта (инерционный, с запаздыванием).

c)  Виды прогнозирующих САР (САР Смита, САР Ресвика и их модификации).

d)  Показатели качества регулирования.

Требуется:

1)  Выбрать прогнозирующий закон регулирования.

2)  Определить настроечные коэффициенты прогнозирующей САР.

3)  Построить переходные процессы.

4)  Оценить показатели качества регулирования.

5)  Проанализировать влияние вариации коэффициентов модели ОУ на показатели качества.

6)  Сделать сравнительный анализ прогнозирующей САР и САР с типовым законом регулирования.

3.1 Синтез прогнозирующей САР.

В качестве прогнозирующей САР используем систему управления предложенную Дж.М.Смитом, которая известна как САР Смита. Представим САР Смита в варианте [6,214-216].

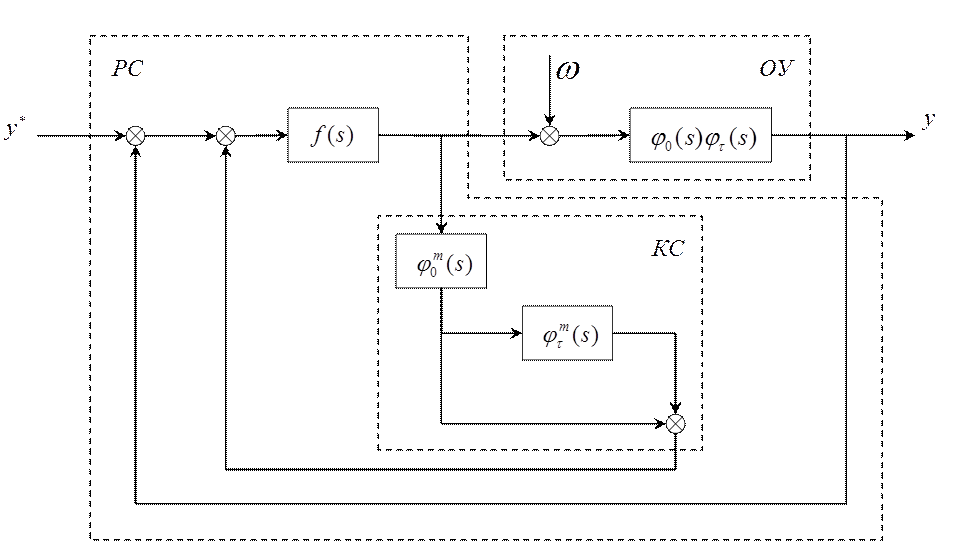
Рисунок 3.1. САР Смита.

где ОУ – объект управления; КС – компенсатор (прогнозатор) Смита; РС – регулятор Смита;  - оператор закона регулирования;  - рациональная часть оператора ОУ;  - оператор запаздывания ОУ; и  - модельная реализация соответствующих операторов.

С помощью эквивалентных структурных преобразований при условии адекватности модели, т.е. и , от схемы рис. 3.1 несложно перейти к схеме рис. 3.2.

Из структурной схемы САР Смита (рис. 3.2) следует:

                                                                                                 (3.1)

                                                                                                    (3.2)

                                                                                         (3.3)

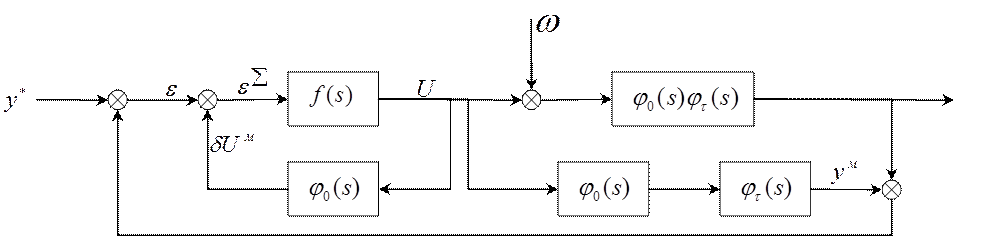
Рисунок 3.2. Модифицированная структура САР Смита.

Формула (3.3) показывает, что  есть запаздывающая на интервал времени  оценка , преобразованная в масштабе одного выходного воздействия, т.е. это оценка неконтролируемого возмущения.

 - прогнозируемые на интервал времени  эффекты управляющих воздействий, а регулирующий блок  направляется суммой сигналов ()  о оценки возмущения , о задающем воздействии и эффектов уже реализованных воздействий. На основе этой суммы и вырабатывается управляющие воздействие.

Одним из недостатков САР Смита является то, что удолетворительная точность управления достигается в том случае, если на интервале запаздывания  приведенное возмущение  изменится незначительно. Для уменьшения этого недостатка необходимо экстраполировать  на интервал времени , т.е. ввести оператор  (рис. 3.3).

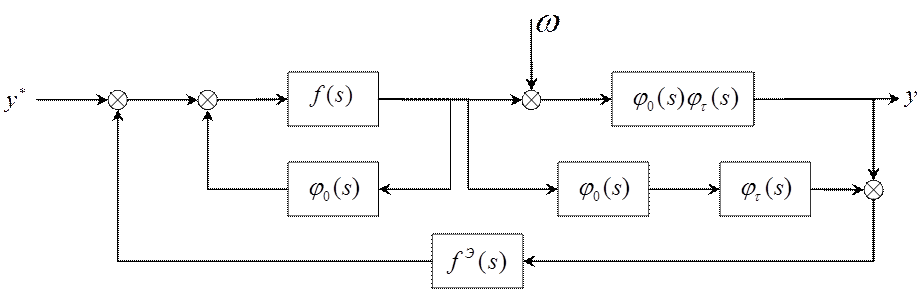
Рисунок 3.2. САР Смита с экстраполятором.