1)
 Этот метод рассматривается для систем, имеющих следующею
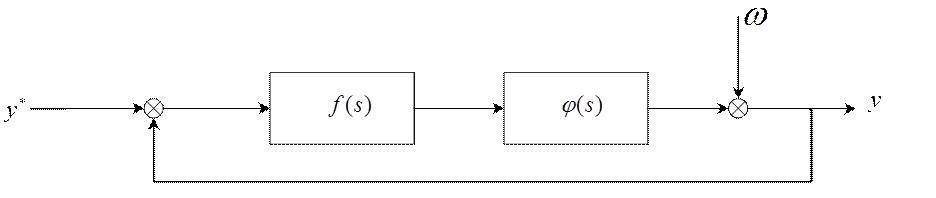
структурную схему (рис. 2.1).
Этот метод рассматривается для систем, имеющих следующею
структурную схему (рис. 2.1).
Рисунок 2.1. Структура САР с возмущением, проведенным к выходу.
Где ![]() -
вектор задающих воздействий,
-
вектор задающих воздействий, ![]() - оператор регулятора,
- оператор регулятора, ![]()
![]() - оператор ОУ,
- оператор ОУ, ![]() - приведенное возмущение.
- приведенное возмущение.
2)
Для систем (рис.
2.1) частотная характеристика замкнутого контура должна быть приблизительно
равна 1 по задающему входу, что необходимо для выполнения равенства ![]() (2.1).
(2.1).
3) Высокую динамическую точность можно получить, если время чистого запаздывания (транспортного запаздывания) относительно очень мало. Оценить значение времени чистого запаздывания можно по спаду автокорреляционной функции приведенного возмущения, который должен быть не ниже 0.7.
С учетом этих предпосылок для получения оптимального закона регулирования можно использовать формулу (2.2).
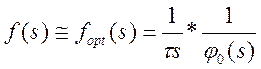 (2.2)
(2.2)
где ![]() – оператор аппроксимирующий ОУ без учета
запаздывания.
– оператор аппроксимирующий ОУ без учета
запаздывания.
Получим оптимальный закон регулирования для данного ОУ:
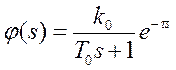 (2.3)
(2.3)
Следовательно
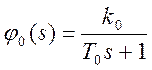 (2.4)
(2.4)
Решим совместно уравнения (2.3) и (2.4)
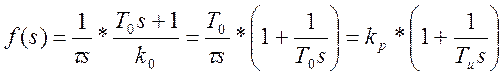 (2.5)
(2.5)
где 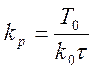 (2.6) -
коэффициент передачи регулятора;
(2.6) -
коэффициент передачи регулятора; ![]() (2.7) - постоянная
интегрирования (время изодрома) регулятора.
(2.7) - постоянная
интегрирования (время изодрома) регулятора.
Исходя из полученного оператора (2.5), можно сделать вывод, что в данной САР будет реализоваться ПИ – алгоритм регулирования. Регулятор с таким алгоритмом осуществляет перемещение регулирующего органа пропорционально отклонению регулируемой величины и интегралу от отклонения.
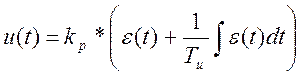 (2.8)
(2.8)
где ![]() - ошибка или рассогласование
системы.
- ошибка или рассогласование
системы.
Оценим значение настроечных коэффициентов закона регулирования, исходя уравнений (2.6), (2.7) и системы (1.2).
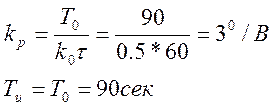
Следовательно
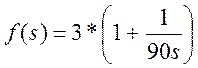 (2.9)
(2.9)
Таким образом получили САР с типовым законом регулирования со структурной схемой рис. 2.2.
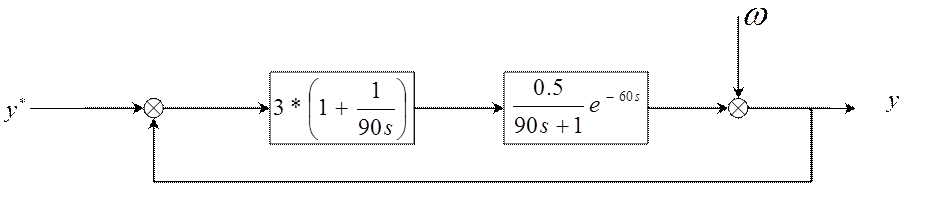 |
Рисунок 2.2 Структурная схема САР с типовым законом регулирования для объекта (2.3).
2.2 Исследование устойчивости САР.
Так как в данной САР объект управления включает в себя звено запаздывания, то для оценки устойчивости применим критерий Найквиста. Существует 2 формулировки этого критерия.
1) Замкнутая система будет устойчива при устойчивой разомкнутой системе в том случае, когда годограф разомкнутой системы не охватывает точку с координатой (-1;j0).
Оператор разомкнутого контура для нашего случая имеет вид
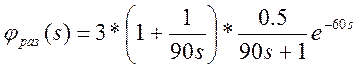 (2.10)
(2.10)
Из выражения (2.10) видно, что характеристическое уравнение имеет один нулевой корень и следовательно разомкнутая система находится на границе устойчивости, поэтому невозможно применить 1 формулировку критерия Найквиста. Рассмотрим 2 определение критерия.
2)
При неустойчивой
разомкнутой системе замкнутая система будет устойчива, если годограф
разомкнутой системы охватывает точку с координатой (-1;j0) ![]() раз, где
раз, где ![]() -
число правых корней в характеристическом уравнении разомкнутого контура.
-
число правых корней в характеристическом уравнении разомкнутого контура.
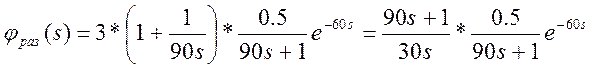 (2.11)
(2.11)
![]() (2.12)
(2.12)
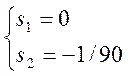 (2.13)
(2.13)
Как видно из решения
характеристического уравнения (2.13) ![]() , а годограф
разомкнутого контура (рис. 2.3) охватывает точку (-1;j0) 0 раз, следовательно можно сделать вывод, что данная САР
устойчива.
, а годограф
разомкнутого контура (рис. 2.3) охватывает точку (-1;j0) 0 раз, следовательно можно сделать вывод, что данная САР
устойчива.
Определим запас
устойчивости по модулю m и по фазе ![]() .
.
1. Запас устойчивости по модулю.
Запас устойчивости по модулю позволяет вычислить дополнительное усилие разомкнутой системы оставляющие замкнутую систему в границах устойчивости.
![]() (2.14)
(2.14)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.