Дифференциальные уравнения и передаточные функции звеньев САУ. Линеаризация нелинейных статических характеристик и нелинейных уравнений. Типовые динамические звенья САУ. Анализ процессов линейных систем

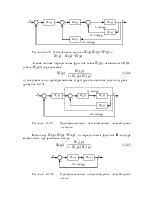
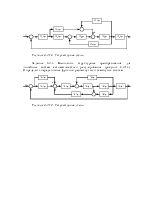
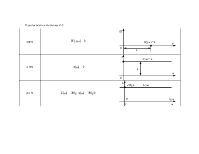
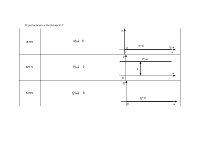
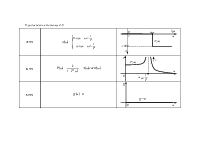
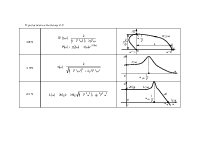
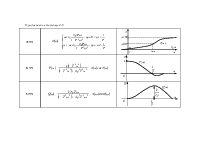
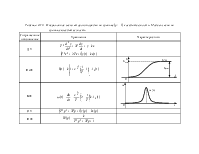
Если система содержит m идеальных дифференцирующих звеньев, то низкочастотная асимптота пересекает ось частот при чистоте:

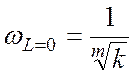.                                           (5.1.4)

3. Провести низкочастотную асимптоту с наклоном -20 или с наклоном +20m. Через точки соответственно по  или .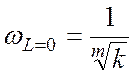

Если система статичная (m==0), то наклон низкочастотной асимптоты равен нулю и она отстоит от оси частот на величину 20lgk.

4. При частотах сопряжения  производить излом ЛАХ, изменяя наклон L() в зависимости от типа звена:

а) для периодических звеньев излом производится на -20дБ/дек;

б) для формирующих звеньев первого порядка излом производится на +20дБ/дек;

в) для колебательных звеньев излом производится на -40дБ/дек;

г) для формирующих звеньев второго порядка излом производится на +20дБ/дек.

5. Пользуясь кривыми поправок (номограммы отклонения)(5.1.1 и 5.1.2), уточнить полученную асимптотическую ЛАХ. Поправки для звеньев, частоты сопряжение которых отличается друг от друга не более чем 2-3 октавы, сила бывает алгебраически

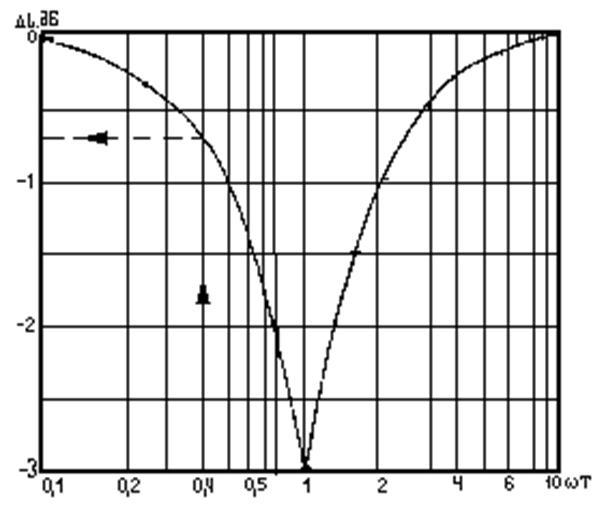Рисунок 5.1.1 - Номограммы для уточнения отклонение точной ЛАХ апериодического звена от асимптотической

Фазовая частота характеристика разомкнутой одноконтурной системы определяется как сумма систем ФЧХ каждого типового звена на фиксированных частотах

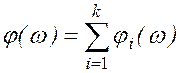.                                         (5.1.5)

Пример 5.1.1. Построить ЛАХ и ЛФХ системы автоматического управления, если передаточная функция разомкнутой системы имеет вид

,                    (5.1.6)

где k=100 c^-1; =1,8 с; Т₁=0,6 с; =0,35; Т₂=0,1 с; =0.05 с.

Решение.

Частоты сопряжения

;

;

.

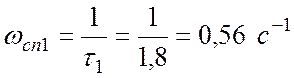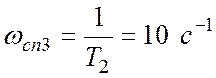Частота при которой низкочастотного асимптоты пересекает ось частот

-20=-20

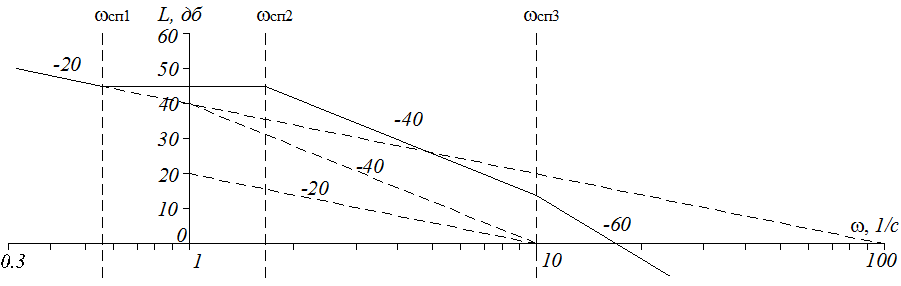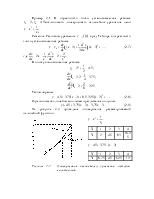
Рисунок 5.1.3 - ЛАХ системы

Максимальное отношение точной ЛАХ от асимптотической для колебательного звена имеет место при =1,66 и равно

.              (5.1.7)

()

()

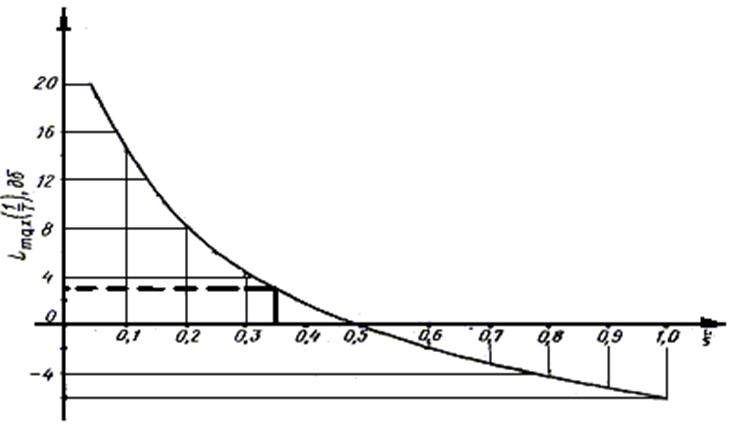Рисунок 5.1.4 - Номограмма для определения резонансного типа ЛАХ колебательного звена.

Пример 5.1.2. Для апериодического звена 1-вого порядка с передаточной функцией

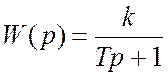.                                          (5.1.8)

Показать, что

1)  точки ЛАХ 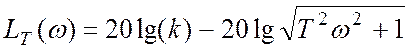 имеет две асимптоты;

2)  частоты сопряжения асимптотической ЛАХ L_a()=;

3)  наклон одной асимптоты 0 дБ/дек имеют второй –{-20дБ/дек}

4)  наибольшее отклонение асимптотической ЛАХ L_a() от точной L_Т() не превышает 3дБ.

Решение.

АЧХ звено 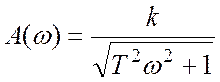,следовательно выражение для такой ЛАХ имеет вид:

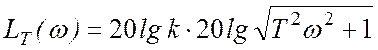.                          (5.1.9)

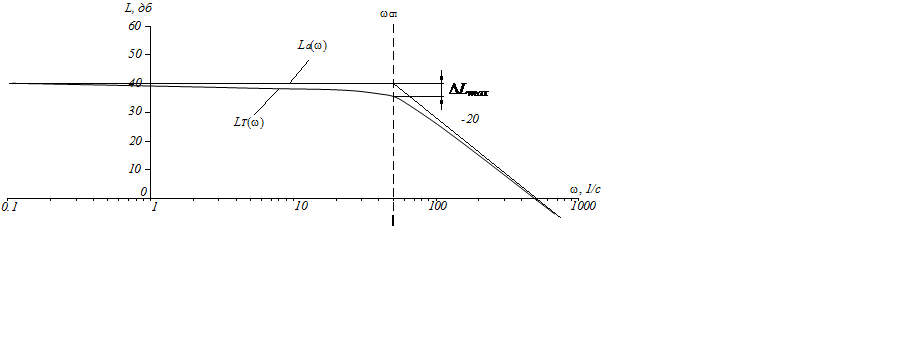Рисунок 5.1.5 - Логарифмические характеристики апериодического звена первого порядка

Если <<1, то произведениям  можно пренебречь и в этом случае получим:

L₁()20lgk,                                          (5.1.10)

поскольку lg1=0.

При <<1, единицей можно пренебречь, тогда подкоренное выражение равно и ЛАХ имеет вид:

L₂()=20lgk - 20lg().                               (5.1.11)

Так как при <<1, точная ЛАХ L_T() стремится к значению L₁()=20lgk, а при >>L_T() приближается к прямой L₂()=20lgk-20lg(), поэтому прямые L₁()=20lgk и L₂()=20lgk-20lg() можно рассматривать как низкочастотную и высокочастотную асимптоты для точной ЛАХ .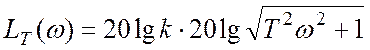

Наклон низкочастотной асимптоты L₁()=20lgk составляет 0 дБ/дек очевиден. Для определения наклона асимптоты L₂()=20lgk-20lg() следует найти разность ординат при изменении частоты на одну декаду, т.е.

L= L₂()-L₂(),                                  (5.1.12)

причем .

Подставив значение частоты, получим:

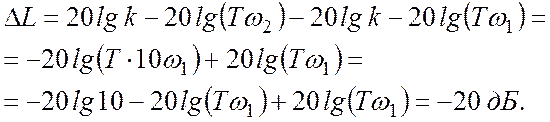          (5.1.13)

Таким образом при изменении частоты на одну декаду изменение ординаты составляет -20дБ, следовательно наклон асимптоты L₂()=20lgk-20lg() составляет -20дБ.

Асимптоты L₁() и L₂() пересекаются в точке, для которой

L₁()= L₂() или 20lgk =20lgk - 20lg(T).               (5.1.14)

Таким образом для точки пересечения асимптот справедливы равенства:

20lg()=0, т.е. =1.                               (5.1.15)

Таким образом, частота сопряжения .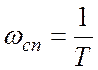

Наибольшее отклонение точной ЛАХ L_T() от асимптотической L_а() имеет место, когда неравенства <<1 и >>1 обращаются в равенство, т.е. при частоте сопряжения.

=1.                                             (5.1.16)

Значение асимптотической ЛАХ при частоте сопряжения

L_а()= L₁()= 20lgk.                           (5.1.17)

Значение точной ЛАХ при :

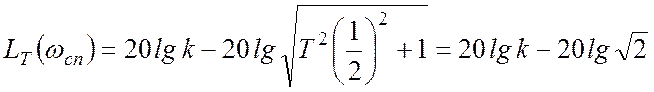.  (5.1.18)

Следовательно

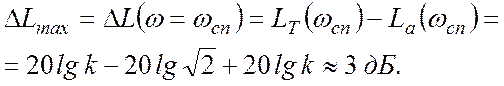            (5.1.19)

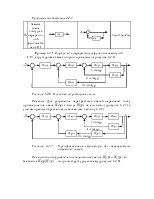
5.2 Логарифмические характеристики замкнутых и многоконтурных систем

Построение логарифмических частотных характеристик замкнутых систем при единичной отрицательной обратной связи, целесообразно производить с помощью номограммы замыкания.

В прямоугольной системе координат номограммы замыкания откладываются значения ЛАХ L() и ЛФХ  разомкнутой системы, соответствующие значения ЛАХ L₃() и ЛФХ  замкнутой единичной отрицательной обратной связью снимается в криволинейных координатах.

Для построения ЛАХ и ЛФХ замкнутой системы с помощью номограммы замыкания следует:

1)  построить ЛАХ и ЛФХ разомкнутой САУ;

2)  в требуемом диапазоне частот снять значения логарифмических частотных характеристик разомкнутой системы L() и ;

3)  для каждого фиксированного значения частоты  в прямоугольной системе координат номограммы замыкания, нанести точку с координатами L() и ;

4)  снять в прямолинейной системе координат значения ЛАХ L() и ЛФХ  замкнутой системы.

5)  если ЛФХ  разомкнутой системы меняется в пределах , то значения  откладывается непосредственно по оси абсцисс номограммы замыкания, а при определенных ЛФХ замкнутой системы следует учитывать, что значения  и  совпадают.

6)  если  меняется в пределах  то по оси абсцисс номограммы замыкания следует откладывать значения