Модернизация котельного агрегата “Тампелла” (СРК-11,12), страница 7

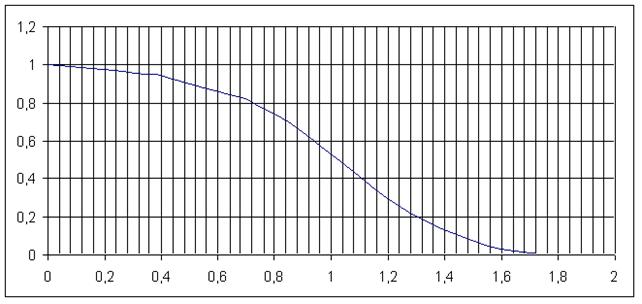
заполняем таблицу 2:

Подсчитываем сумму столбца 4 . затем столбца 6

определяем интегральные площади F2 и F3

 

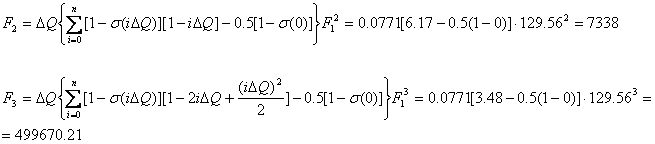
Определяем ошибку аппроксимации ∆ .

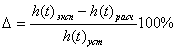
Вывод: данный метод аппроксимации позволяет определить передаточную функцию объекта с погрешностью ∆ <1%

2.3. Определение передаточной функции объекта методом последовательного логарифмирования.

Так как переходная характеристика объекта является монотонно возрастающей то ее можно представить в виде:

1. Переносим начало координат в точку 0^’ .

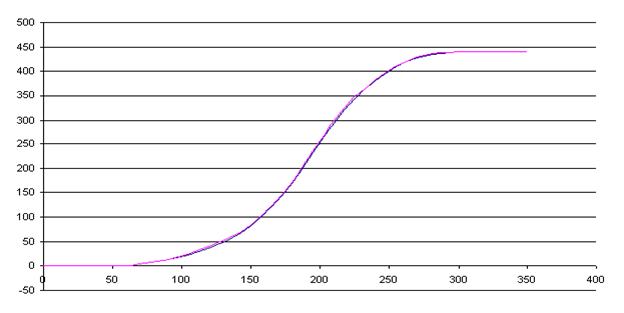
Переходная характеристика.

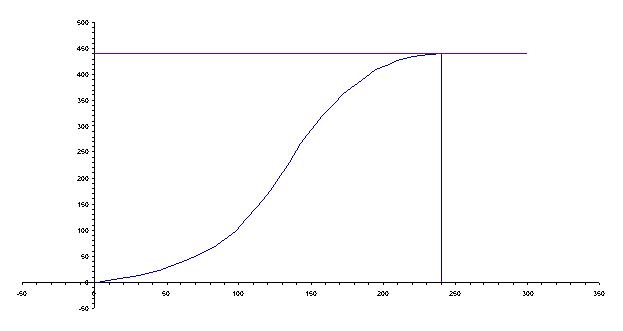
τ_тр=60 мин.

С₀=h(∞)=440.

Производим разбиение кривой прямыми линиями параллельными оси абсцисс на участки ∆h_i(t)

так чтобы h_i(t)/h_i+1(t)=0,9.

2. Определяем  разницу h(∞)-h_i(t) и строим кривую разгона в логарифмическом масштабе.

Таблица 1. 

h(t)*0,9	0,000	11,014	12,238	13,597	15,108	16,787	18,652	20,725	23,027	25,586	28,429	31,588	35,097
F1	440	428,986	427,762	426,403	424,892	423,213	421,348	419,275	416,973	414,414	411,571	408,412	404,903
lg[F1]	2,643	2,632	2,631	2,630	2,628	2,627	2,625	2,622	2,620	2,617	2,614	2,611	2,607
t, мин.	0	29,5	32,0375	34,575	37,1125	39,65	42,1875	44,725	47,2625	49,8	51,4	54,8	57,2