Параметрический синтез системы автоматического регулирования, страница 4

В момент времени t_i амплитуда колебаний      ,

а в момент времени t_i+2:         

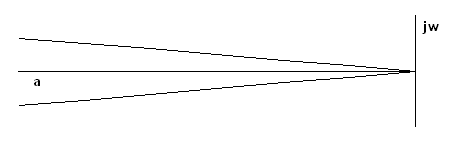Величину 2πm называют логарифмический декремент затухания колебаний.

     tg g = m , т.е. получаем, что  g = arctg m.

Степень затухания рассматриваемой составляющей процесса будет определяться значением тангенса этого угла. Если корень характеристического уравнения этой системы будет лежать в плоскости комплексного переменного на линии АОВ , то степень затухания Y будет постоянной.

Выражение передаточной функции W(P) звеньев, для которых р_к находится на линии АОВ, называется расширенной АФЧХ:

W (m, jw) = A (m, jw) * e^ -j( j (m, jw))

Если m = 0, то РАФЧХ совпадает с линией АОВ и совмещается с мнимой осью, следовательно, АОВ – мнимая ось, а система находится на границе устойчивости.

При расчете устойчивости системы используется соотношение:

W (m, jw)_об * W (m, jw)_р = 1

Для ПИ-регулятора это соотношение будет иметь вид:

W (m, jw) = ( m * C₀ / [ w * (m² + 1)] – C₁ + j * C₀ / [ w * (m² + 1)]

Построив в плоскости настроечных параметров регулятора линию, равную степени колебательности, выбираем на ней различные точки с конкретными значениями параметров регулятора, обеспечивающими оптимальный процесс регулирования.

Для системы регулирования, рассматриваемой в дипломном проекте, ранее были получены следующие данные:

a)  передаточная функция объекта   W(p)_об=110е^-0,7р/(3,5p +1)

b)  передаточная функция регулятора

W_р(p)=-(0,0179+0,0413р)/p

  Произведя в формулах замену p=w*(j–m), получаем расширенные АФЧХ:

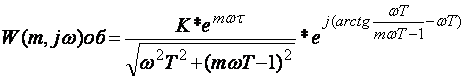
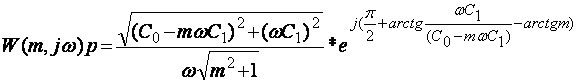
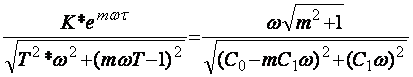
    Решаем систему относительно С₀ и С₁:

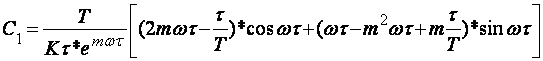
Подставляя различные частоты от 0 до значения, при котором С₀ становится отрицательным, строим зависимость С₀=f(C₁): для этого заполняем таблицу  и в EXCEL строим график.

Таблица 5.2

ω	m	C0	C1	Ти
0,000	0,221	0,000	-0,009	0,000
0,100	0,221	0,000	-0,007	-18,542
0,200	0,221	0,001	-0,005	-3,292
0,300	0,221	0,003	-0,002	-0,723
0,400	0,221	0,006	0,001	0,097
0,500	0,221	0,008	0,004	0,446
0,600	0,221	0,011	0,007	0,624
Продолжение табл. 5.2
ω	m	C0	C1	Ти
0,700	0,221	0,014	0,010	0,730
0,800	0,221	0,017	0,014	0,802
0,900	0,221	0,020	0,017	0,860
1,000	0,221	0,023	0,021	0,914
1,100	0,221	0,025	0,025	0,969
1,200	0,221	0,027	0,028	1,032
1,300	0,221	0,028	0,031	1,108
1,400	0,221	0,029	0,034	1,204
1,500	0,221	0,028	0,037	1,331
1,600	0,221	0,027	0,040	1,509
1,700	0,221	0,024	0,042	1,773
1,800	0,221	0,020	0,044	2,204
1,900	0,221	0,015	0,046	3,029
2,000	0,221	0,009	0,048	5,227
2,100	0,221	0,002	0,049	28,378
2,200	0,221	-0,007	0,049	-7,109