Выбор типа регулятора и расчет его настроечных параметров, страница 4

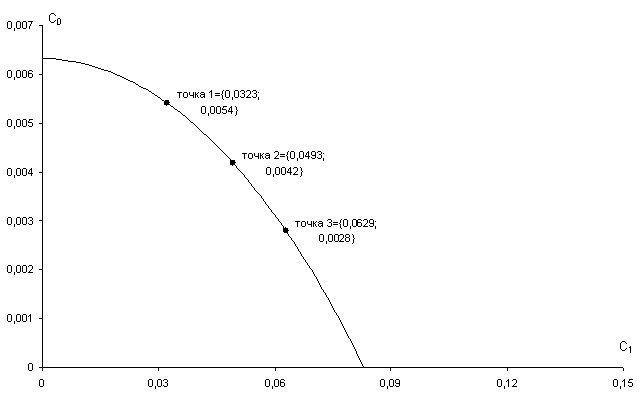
         Рисунок 2.3.6 – Зависимость С₀=f(C₁), при m=0,7

1.  При С₀ = 0,0054; С₁ =0,0323:

.

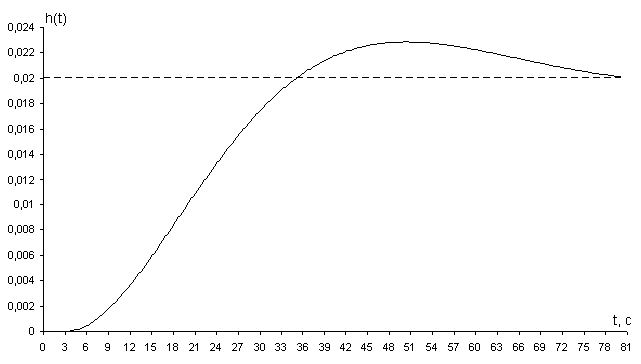
Рисунок 2.3.7 – Переходной процесс замкнутой САР с настройками             регулятора

2.  При С₀ = 0,0042; С₁ =0,0493:

.

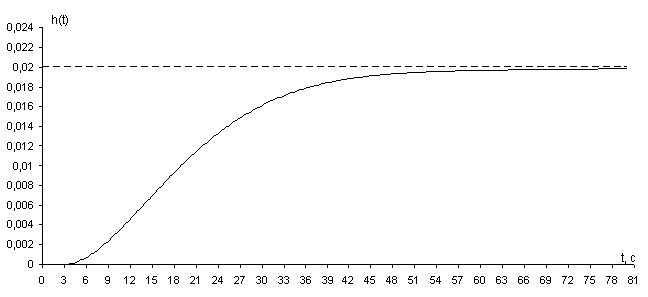
Рисунок 2.3.8 – Переходной процесс замкнутой САР с настройками регулятора

3.  При С₀ = 0,0028; С₁ =0,0629:

.

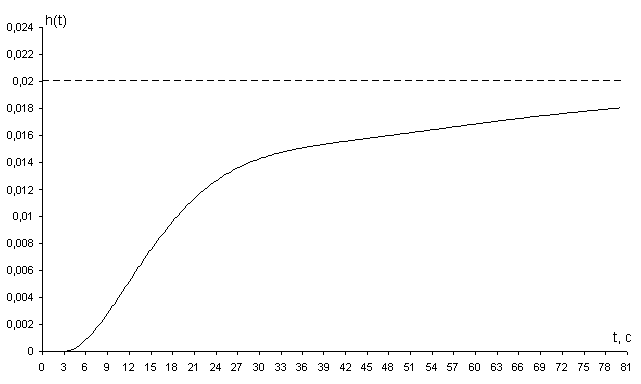
Рисунок 2.3.9 – Переходной процесс замкнутой САР с настройками регулятора

 

Из трех представленных переходных процессов для замкнутой САР, наиболее близким к оптимальному является процесс на рис. 2.3.8, Он удовлетворяет требованиям регулирования, которые были сформулированы, то есть процесс является апериодическим, отклонения температуры происходит в допустимых пределах, время регулирования совпадает с заданным.

Для построения оптимального переходного процесса, и соответственно нахождения оптимальных параметров регулятора построим линию интегрального качества.

2.3.2. Линия интегрального качества

Для построения линии интегрального качества воспользуемся формулой квадратичной интегральной оценки:

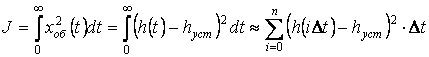
Для построения графика эту оценку необходимо определить при различных значениях частоты ω, а следовательно и различных значениях С₁. На первом этапе выделим на линии равной степени затухания (m = 0,7) точку, которая будет иметь параметры, близкие к оптимальным. Это точка 2={0,0493; 0,0042}. Ей соответствует процесс, представленный на рис. 2.3.8. Возьмем четыре точки до нее и четыре – после нее, и на основании данных параметров определим, используя программный пакет АСОТАР, значения критерия интегрального качества. В результате имеем следующую таблицу значений:

 

Таблица 2.15