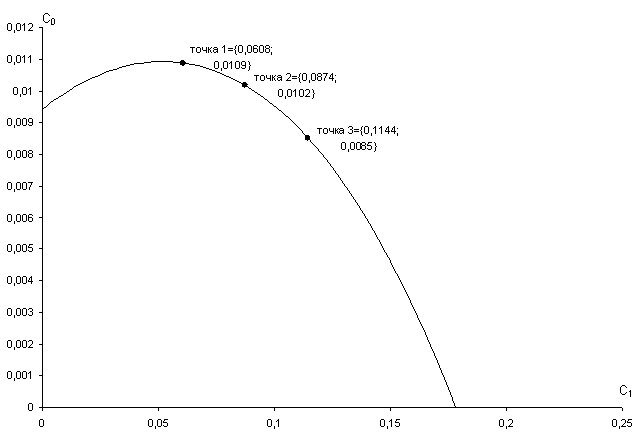
Другие предметы \ Основы автоматики и системы автоматического управления

Выбор типа регулятора и расчет его настроечных параметров, страница 3

Рисунок 2.3.2 – Зависимость Со=f(С1), при m=0,366

С помощью графика на рис. 2.3.2. выбираем конкретные значения С0 и С1, для которых определяем коэффициент регулирования kр и время интегрирования Tи (время дифференцирования Tд = 0, так как ПИ-закон регулирования) и строим переходные процессы для полученных настроечных параметров.

1.  При С0 = 0,0109; С1 =0,0608:

.

  

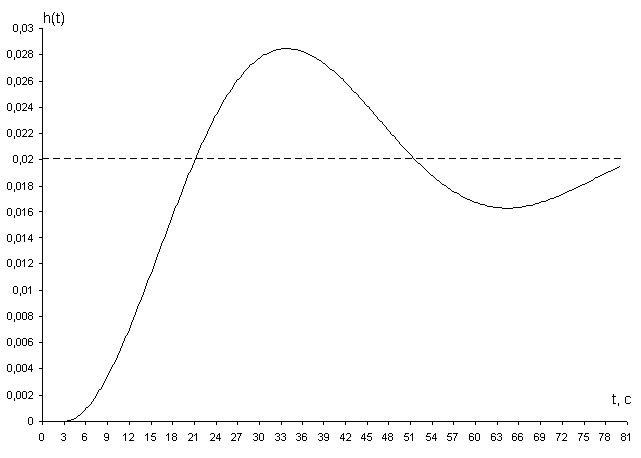
Рисунок 2.3.3 – Переходной процесс замкнутой САР с настройками  регулятора

2.  При С0 = 0,0102; С1 =0,0874:

.

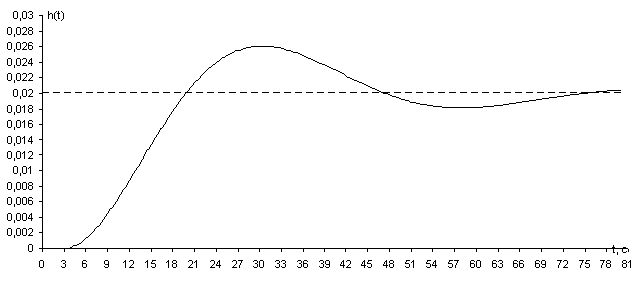
Рисунок 2.3.4 – Переходной процесс замкнутой САР с настройками регулятора

3.  При С0 = 0,0085; С1 =0,1144:

.

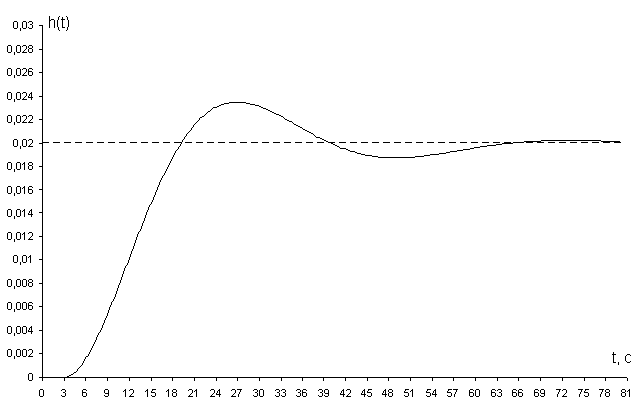
Рисунок 2.3.5 – Переходной процесс замкнутой САР с настройками регулятора

Видно, что из трех представленных переходных процессов для замкнутой САР, нет процесса, который  удовлетворял бы требованиям регулирования. Следовательно, делаем вывод о том, что взятая нами степень колебательности m = 0, 366 не подходит.

Возьмем степень колебательности m = 0,7, что соответствует значению степени затухания y = 0,988. Исходя из новых условий, получим:

;

;

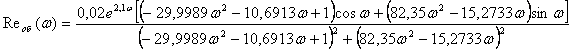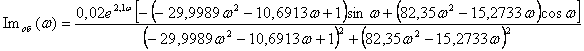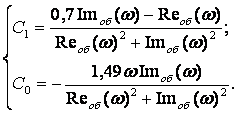
Построим в координатах С0, С1 зависимость С0 = f(С1) для выбранной степени колебательности m = 0,7, при этом выбираем такие значения частоты ω, чтобы С0 и С1 были больше нуля:

Таблица 2.14

w

C0

C1

w

C0

C1

w

C0

C1

0,092473

0,006333

1E-07

0,109

0,005666

0,027253

0,126

0,003532

0,056115

0,093

0,00633

0,000848

0,11

0,005583

0,028937

0,127

0,003355

0,057819

0,094

0,006323

0,00246

0,111

0,005495

0,030623

0,128

0,003173

0,059523

0,095

0,006311

0,004079

0,112

0,005403

0,032312

0,129

0,002985

0,061226

0,096

0,006294

0,005704

0,113

0,005305

0,034004

0,13

0,002791

0,062928

0,097

0,006274

0,007334

0,114

0,005201

0,035697

0,131

0,002591

0,064629

0,098

0,006249

0,008969

0,115

0,005093

0,037392

0,132

0,002385

0,066329

0,099

0,006219

0,01061

0,116

0,004979

0,039089

0,133

0,002172

0,068028

0,1

0,006185

0,012256

0,117

0,004859

0,040788

0,134

0,001954

0,069725

0,101

0,006146

0,013906

0,118

0,004734

0,042488

0,135

0,001729

0,071421

0,102

0,006103

0,015561

0,119

0,004604

0,044189

0,136

0,001499

0,073115

0,103

0,006055

0,01722

0,12

0,004468

0,045891

0,137

0,001262

0,074806

0,104

0,006002

0,018883

0,121

0,004326

0,047594

0,138

0,001019

0,076496

0,105

0,005945

0,02055

0,122

0,004179

0,049298

0,139

0,000769

0,078183

0,106

0,005883

0,022221

0,123

0,004026

0,051002

0,14

0,000513

0,079867

0,107

0,005815

0,023895

0,124

0,003867

0,052707

0,141

0,000251

0,081549

0,108

0,005743

0,025573

0,125

0,003702

0,054411

0,14193

1,73E-06

0,083111
Скачать файл