Информационно-безопасные системы. Анализ проблемы: Учебное пособие, страница 38

Примечание. Событие отсутствия ошибки в последовательности f_i названо в работе [5] "ошибкой нулевой кратности". Поэтому фактическое число необнаруживаемых оши­бок равно 2^k - 1. В каждой из всех остальных 2^m – 1строк записано по 2^k ошибок. Кратность всех ошибок первой строки (за исключением ошибки нулевой кратности) не менее кодового расстояния, т.е.

t_но ³ d                                                          (9.6)

Таким образом, используя указанные свойства ПТС, находим

γ_но=(2^k - 1) / (2ⁿ – 1) » 2^k / 2ⁿ = 1 / 2^m;                                     (9.7)

d  = 1 - γ_но = 1 – 1 / 2^m,                                           (9.8)

где m - степень порождающего многочлена g(x) (m = n - k).

Для первого и второго вариантов контроля γ_но и d можно найти, если учесть, что ошибки при использовании этих вариантов, не могут попадать на контрольные последовательности, а могут происходить только в последовательностях s_i, длины k. Пoэтoму количество возможных ошибок для любого из этих вариантов равно 2^k, а число различ­ных остатков r_ki равно 2^m. Следовательно, число необнаруживаемых ошибок равно 2^k / 2^m и доля необнаруживаемых ошибок

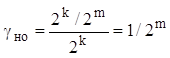                                                  (9.9)

d = 1 – 1 / 2^m                                               (9.10)

т. е. γ_но и d зависят только от степени порождающего многочлена g(x), как для первого и второго вариантов.

Однако необходимо учесть, что общее число возможных ошибок уменьшилось от 2ⁿ до 2^k , а число необнаруживаемых ошибок - от 2^k до 2^k / 2^m за счет принятия специальных организационных мер (хранения последовательностей r_эki вне памяти ЭВМ). Если общее число всех возможных ошибок принять таким же, как в первом и втором ва­риантах, т.е. 2ⁿ, то

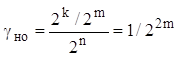                                     (9.11)

d = 1 – 1 / 2^2m                                              (9.12)

т.е. коэффициент γ_но, уменьшился по сравнению с первым и вторым вариантами в 2^m раз за счет сокращения множества всех ошибок до 2^k. В этих вариантах доля необнаруживаемых ошибок подсчитывается по отношению к ошибкам, записанным в верхней строке ПТС. Из этих ошибок верхней строки не обнаруживает доля γ_но= 1 / 2^m. В пер­вом и втором вариантах ни одна из таких ошибок не может обнаруживаться.

9.4. Экспериментальные данные и выводы

Достоверность контроля была проверена экспериментально. В эксперименте исследовались коды, получаемые при помощи многочлена g(x) = х¹⁰ + х³ + 1 (m=10), информационная часть кодовою вектора изменялась от 32 до 1013, контрольная по­следовательность (эталонная сигнатура) для всех вариантов равнялась десяти, т.е.m=10. С кодом каждой длины производилось 200 000 исследований. Полученные дан­ные сведены в табл.9.1

В память производилась запись случайной последовательности длины в 32 бита, которая имитировала несанкционированную запись. Как видно из данных табл.9.1, ста­тистическая оценка практически не зависит от длины контролируемой последователь­ности k и колеблется около теоретического значения 1/2^m = 0,0009765.

Таблица 9.1

k	Число необнаружений	γно
32	185	9.25 * 10-4 (1 / 1081)
63	199	9.95 * 10 -4 (1 / 1005)
126	181	9.05* 10-4 (1/1105)
253	222	1.11 • 10-3 (1/901)
506	213	1.065 * 10-3 (1/939)
1013	187	9.20 * 10-4 (1 / 1070)

В заключение приведем основные выводы.

1.  Наиболее эффективным способом повышения достоверности обнаружения несанкционированных записей является повышение степени m порождающего многочлена g(x). В пределе при m = k можно обнаружить любую из 2^k ошибок (возможных несанк­ционированных записей в контролируемой последовательности длины k), если приме­нять третий или четвертый варианты контроля. Но при m = k длина эталонных остатков r_эki окажется равной длине контролируемых последовательностей s_i.  В этом случае про­ще хранить копии контролируемых последовательностей и в процессе контроля сравни­вать эти копии с оригиналами. Поэтому необходимо находить разумное соотношение между m и k.