Решения к экзаменационным задачам по дисциплине "Дискретная математика"

Дьяконица С.А.

Задача №31. Линейная дискретная система задана импульсной характеристикой . Определить реакцию системы на входной сигнал , где

Решение:

Чтобы найти реакцию на входной сигнал х(n)=и(п)—и(п—N), в силу  необходимо для получения n-го значения выходной последовательности сформировать произведение x(k)h(n—к) и просуммировать значения получившейся последовательности.

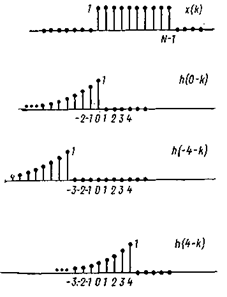
Две составляющие последовательности показаны на рис. как функции k, причем h(n—k) изображена для нескольких значений п. Из этого следует, что при n<0 h(n—k) и x(k) не имеют ненулевых перекрывающихся выборок и, следовательно, y(n)=0 при n<0. При 0<n<N h(n—k) и x(k) имеют ненулевые перекрывающиеся выборки от k=0 до k=n, поэтому при 0£n<N-1

при N-1£n ненулевые перекрывающиеся выборки простираются от k = 0 до k=N—1 и поэтому

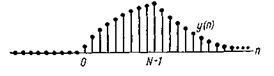
Реакция y(n) изображена на рис.

Задача №32. Линейная дискретная система задана передаточной функцией . Получить импульсную характеристику системы.

Решение:

Дискретная передаточная функция по определению равна , тогда

.

Используя свойство z – преобразования при переходе к оригиналу , получаем разностное уравнение у(п)=ау(п—1)+х(п). Чтобы получить импульсную характеристику, положим х(п)=d(п) при нулевых начальных условиях. Тогда

h(n) = 0, n<0;

h(0)=ah( —1) + 1 = 1;

h(1)=ah(0) =a;

:

h(n)=ah(n—1)=aⁿ.

Таким образом, h(n)=aⁿu(n),

где

Задача №33. Получить разностное рекуррентное уравнение для моделирования системы, заданной передаточной функцией , при интервале дискретизации .

Решение:

Чтобы получить разностное рекуррентное уравнение для моделирования системы, заданной передаточной функцией , необходимо найти дискретный аналог передаточной функции. Для этого воспользуемся билинейным преобразованием, которое позволяет произвести замену оператора Лапласа следующим выражением , тогда

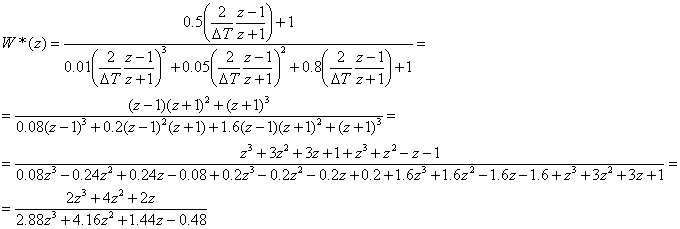По определению

,

тогда

.

Используя свойство z – преобразования при переходе к оригиналу , получаем разностное уравнение