1) Определение структур синтезированного рекурсивного цифрового фильтра.
а) прямая форма:
числитель:
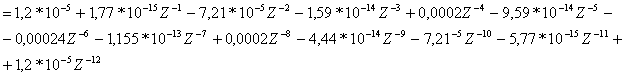 знаменатель:
знаменатель:
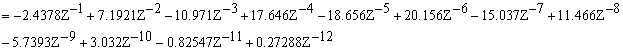
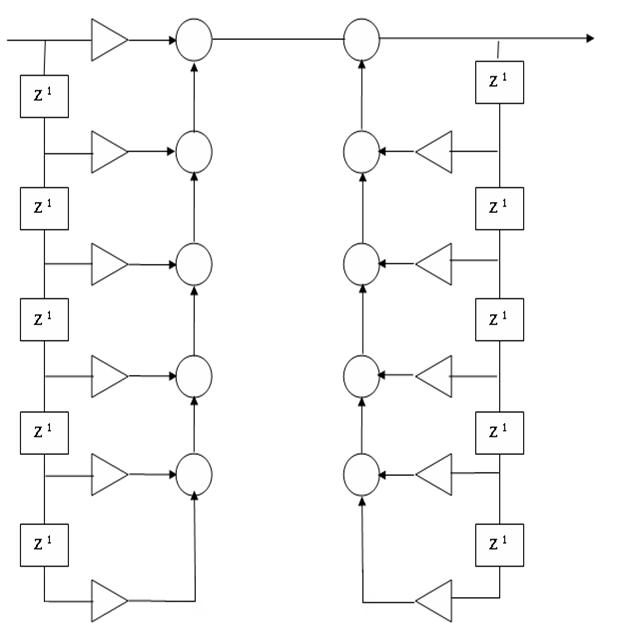
Рисунок 1 - Прямая структура фильтра
б) каноническая форма:
числитель:
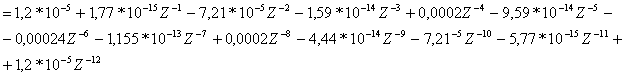 знаменатель:
знаменатель:
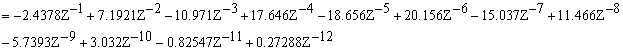
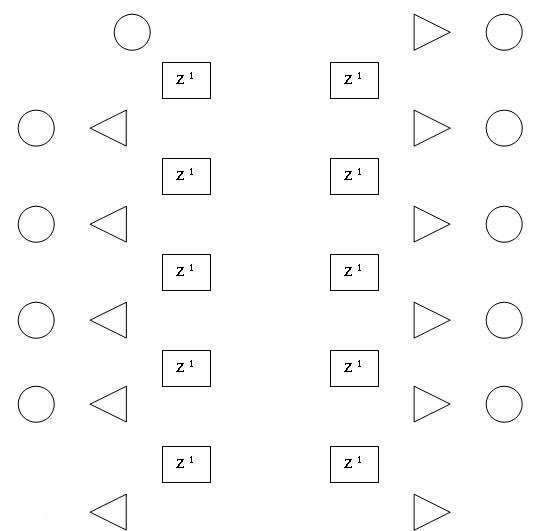
Рисунок 2 - Каноническая структура фильтра
в) каскадная форма:
[s,g]=tf2sos(a,b)
s=1 2.0527 1.0536 1 -0.31625 0.71783
1 1.9992 1.0001 1 -0.46557 0.7228
1 1.9481 0.94897 1 -0.19304 0.78439
1 -2.0324 1.0327 1 -0.61129 0.79489
1 -1.9997 1 1 -0.12432 0.9155
1 -1.968 0.9683 1 -0.72731 0.92138
g=1.2017e-005 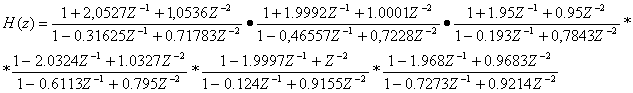
г) параллельная форма:
[r,p,k]=residuez(a,b)
r =0.0337 - 0.0552i
0.0337 + 0.0552i
0.0351 + 0.0602i
0.0351 - 0.0602i
-0.2493 - 0.0141i
-0.2493 + 0.0141i
-0.2642 + 0.0005i
-0.2642 - 0.0005i
0.2046 + 0.4027i
0.2046 - 0.4027i
0.2400 - 0.3941i
0.2400 + 0.3941i
p = 0.3637 + 0.8883i
0.3637 - 0.8883i
0.0622 + 0.9548i
0.0622 - 0.9548i
0.3056 + 0.8375i
0.3056 - 0.8375i
0.0965 + 0.8804i
0.0965 - 0.8804i
0.2328 + 0.8177i
0.2328 - 0.8177i
0.1581 + 0.8324i
0.1581 - 0.8324i
k =4.4038e-005
[a1,b1]=residuez(r(1:2),p(1:2),[])
a1 = 0.0673 + 0.0000i 0.0736 - 0.0000i
b1 = 1.0000 -0.7273 0.9214
[a1,b1]=residuez(r(3:4),p(3:4),[])
a1 = 0.0703 + 0.0000i -0.1194 + 0.0000i
b1 = 1.0000 -0.1243 0.9155
[a1,b1]=residuez(r(5:6),p(5:6),[])
a1 = -0.4986 + 0.0000i 0.1761 - 0.0000i
b1 =1.0000 -0.6113 0.7949
[a1,b1]=residuez(r(7:8),p(7:8),[])
a1 = -0.5284 - 0.0000i 0.0502 + 0.0000i
b1 = 1.0000 -0.1930 0.7844
[a1,b1]=residuez(r(9:10),p(9:10),[])
a1 = 0.4093 + 0.0000i -0.7539 - 0.0000i
b1 = 1.0000 -0.4656 0.7228
[a1,b1]=residuez(r(11:12),p(11:12),[])
a1 = 0.4801 - 0.0000i 0.5801 + 0.0000i
b1 = 1.0000 -0.3163 0.7178
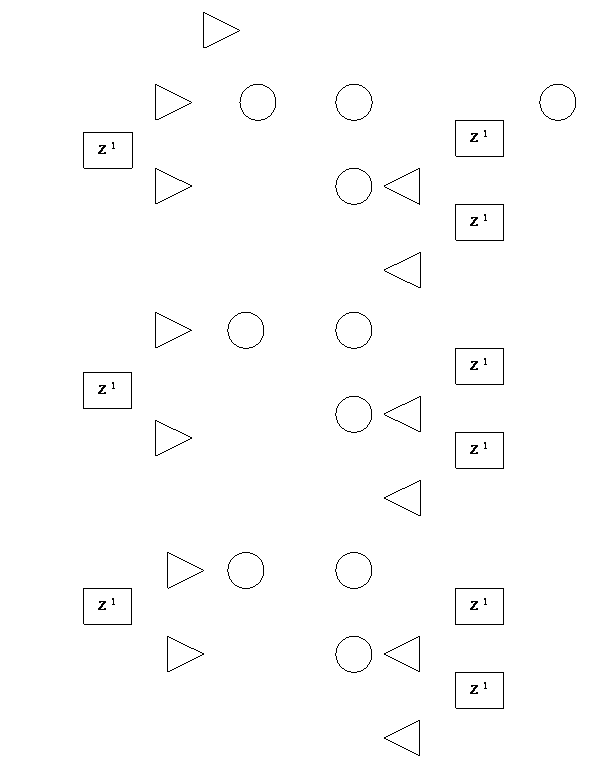
Рисунок 3 - Параллельная структура фильтра
2) Моделирование работы рекурсивного цифрового фильтра.
а) Прямоугольный импульс:
t=0:0.000625:0.125
s=rectpuls(t-0.03125,0.0625);
plot(t,s)
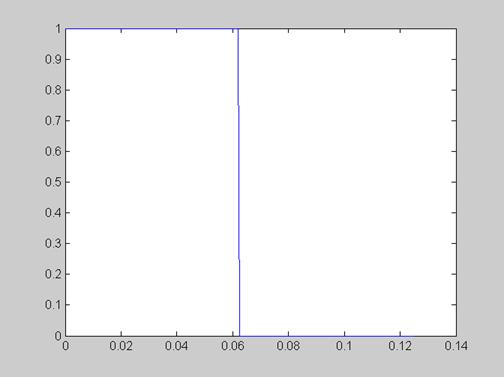
Рисунок 5 - Входное воздействие
y=filter(az,bz,s);
plot(t,s,'r',t,y,'g')
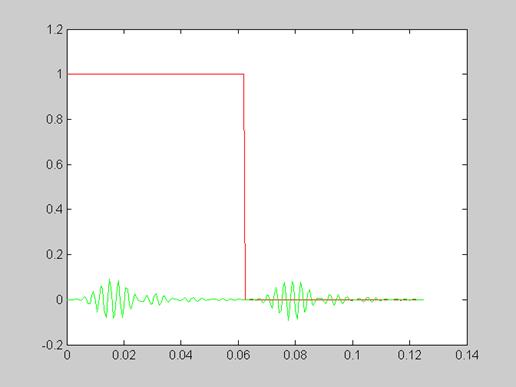
Рисунок 6 -Выходной сигнал, полученный с помощью разностного уравнения
h=impz(az,bz,201);
y=conv(s,h);
plot(t,y(1:201))
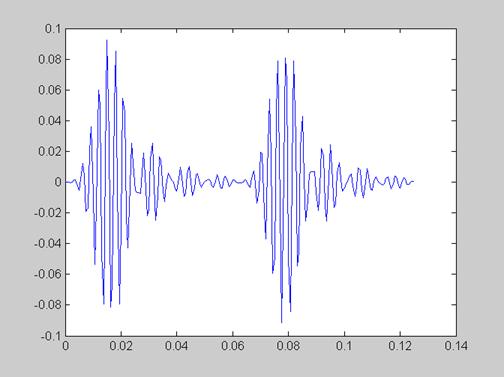
Рисунок 7 - Выходной сигнал, полученный с помощью свёртки
б) Треугольный импульс:
s=tripuls(t-0.035125,0.0625);
plot(t,s)
y=filter(az,bz,s);
plot(t,s,'r',t,y,'g')
h=impz(az,bz,201);
y=conv(s,h);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.