plot(t,y(1:201))
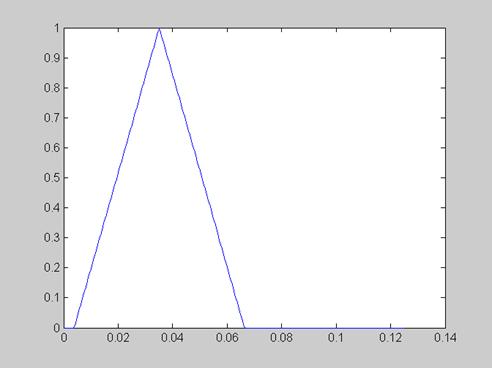
Рисунок 8 -Входное воздействие
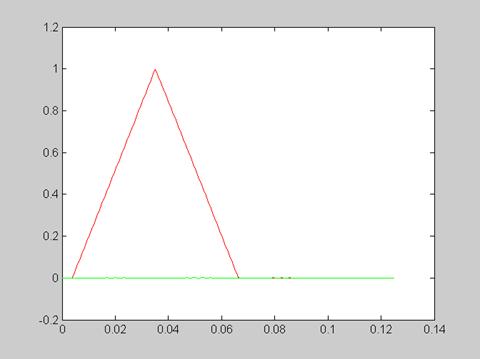
Рисунок 9 - Выходной сигнал, полученный с помощью разностного уравнения
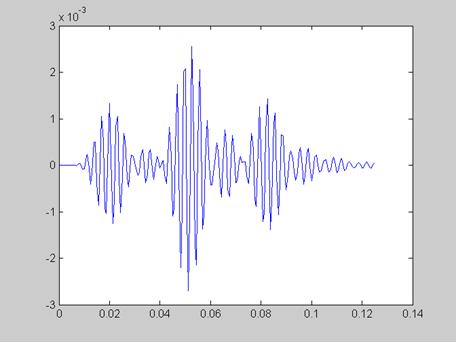
Рисунок 10 - Выходной сигнал, полученный с помощью свёртки
в) Экспоненциальный импульс:
s=exp(-t/0.025)
plot(t,s)
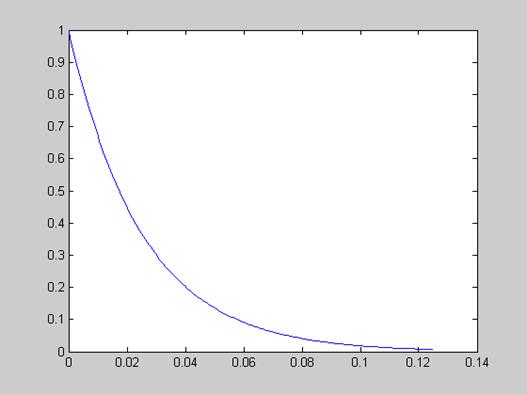
Рисунок 11 - Входное воздействие
y=filter(az,bz,s)
plot(t,s,’r’,t,y,’g’)
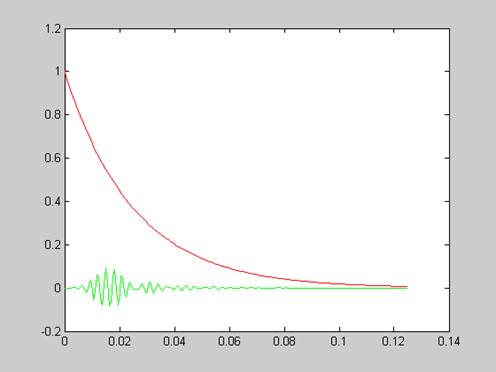
Рисунок 12 - Выходной сигнал, полученный с помощью разностного уравнения
h=impz(az,bz,201)
y=conv(s,h)
plot(t,y(1:201))
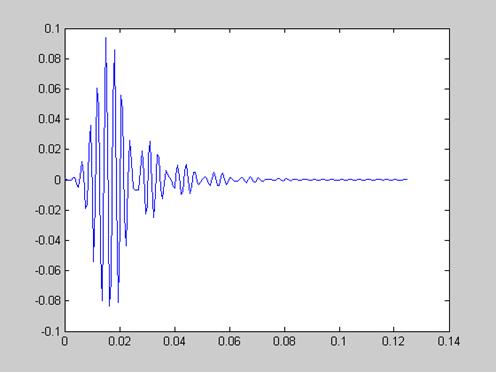
Рисунок 13 - Выходной сигнал, полученный с помощью свёртки
г) синусоидальный импульс.
s=sin(pi*t/0.0625);
plot(t,s)
y=filter(az,bz,s)
plot(t,s,’r’,t,y,’g’)
h=impz(az,bz,201)
y=conv(s,h)
plot(t,y(1:201))
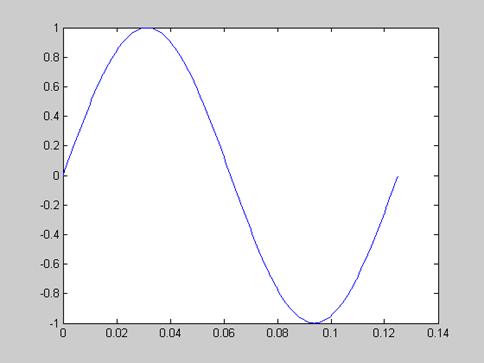
Рисунок 14 - Входное воздействие
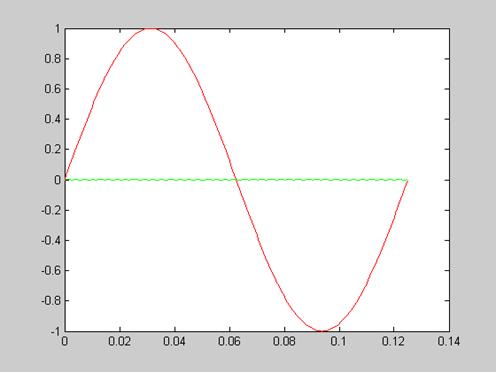
Рисунок 15 - Выходной сигнал, полученный с помощью разностного уравнения
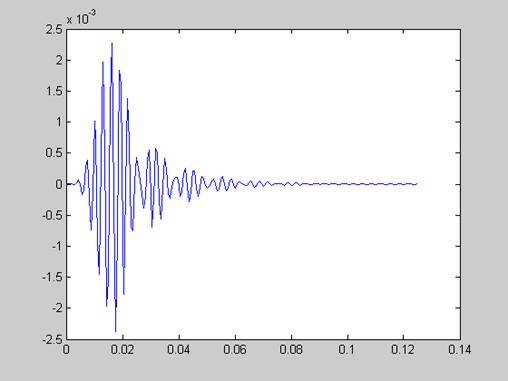
Рисунок 16 - Выходной сигнал, полученный с помощью свёртки
д) на периодическую последовательность прямоугольных импульсов:
s=0.5*(1+square(2*pi*t/0.028,0.014/0.028*100));
plot(t,s)
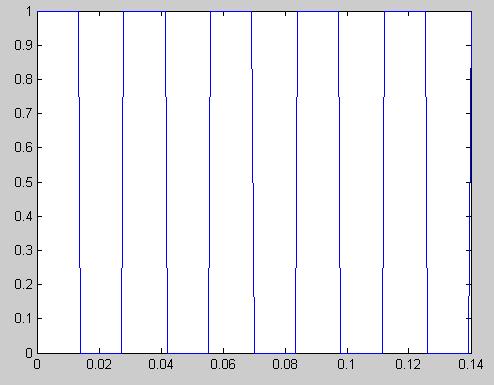
Рисунок 17 - Входное воздействие
y=filter(a,b,s)
plot(t,s,’r’,t,y,’g’)
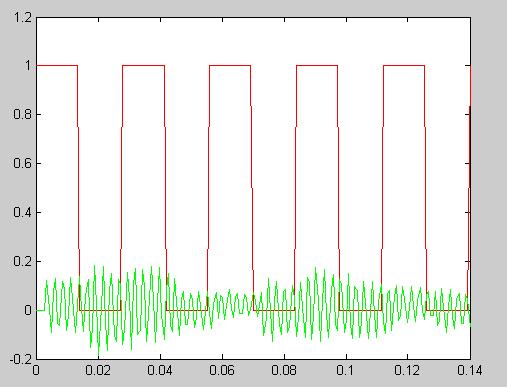
Рисунок 18 - Выходной сигнал, полученный с помощью разностного уравнения
h=impz(a,b,201)
y=conv(s,h)
plot(t,y(1:201))
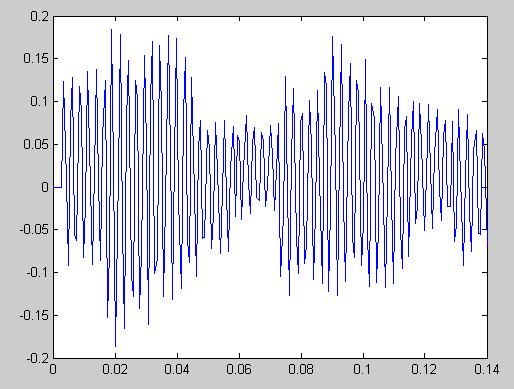
Рисунок 19 - Выходной сигнал, полученный с помощью свёртки
е) На пилообразный сигнал.
s=sawtooth(2*pi*t/0.028);
plot(t,s)
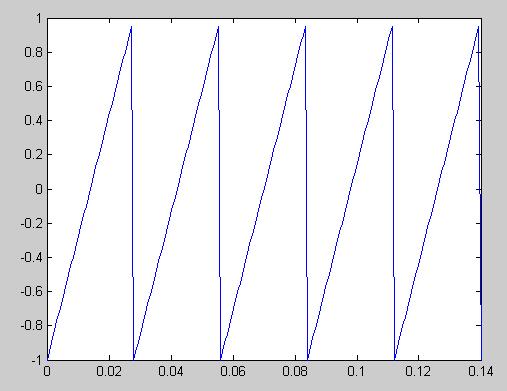
Рисунок 20 - Входное воздействие
y=filter(a,b,s)
plot(t,s,’r’,t,y,’g’)
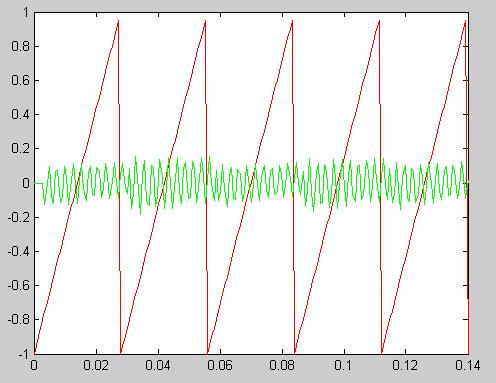
Рисунок 21 - Выходной сигнал, полученный с помощью разностного уравнения
h=impz(a,b,201)
y=conv(s,h)
plot(t,y(1:201))
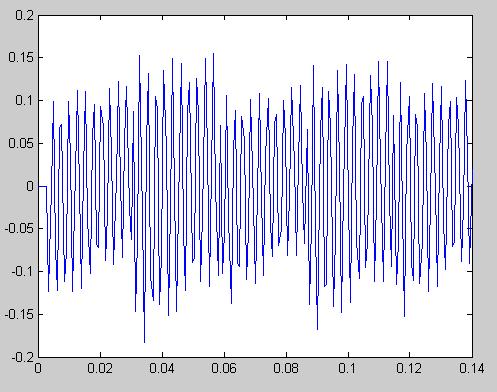
Рисунок 22 - Выходной сигнал, полученный с помощью свёртки
ж) На синусоидальный сигнал:
s=sin(2*pi*130*t)
plot(t,s)
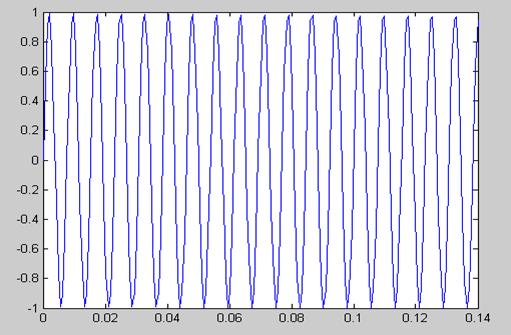
Рисунок 23 - Входное воздействие
y=filter(a,b,s)
plot(t,s,’r’,t,y,’g’)
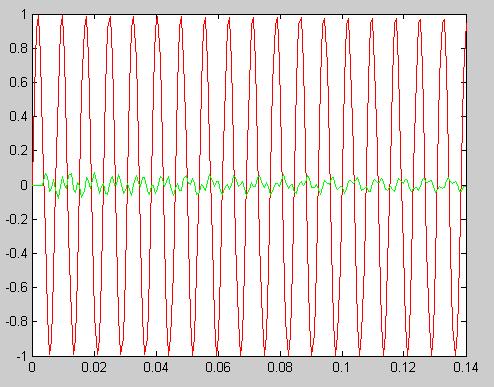
Рисунок 24 - Выходной сигнал, полученный с помощью разностного уравнения
h=impz(a,b,201)
y=conv(s,h)
plot(t,y(1:201))
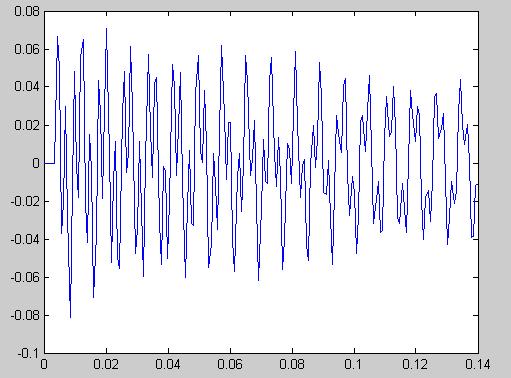
Рисунок 25 - Выходной сигнал, полученный с помощью свёртки
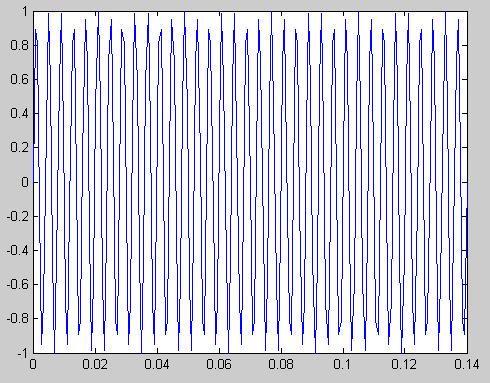
s=sin(2*pi*250*t)
plot(t,s)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.