Синтез и моделирование нерекурсивных фильтров (отчет по лабораторной)

Синтез и моделирование не рекурсивных фильтров.

1. Исходя из заданных данных спроектировать нерекурсивный цифровой фильтр нижних и высоких частот с помощью метода весовых окон.

Фильтр высоких частот

win=bartlett(37);

a=fir1(35,300/700,'high',win);

impz(a)

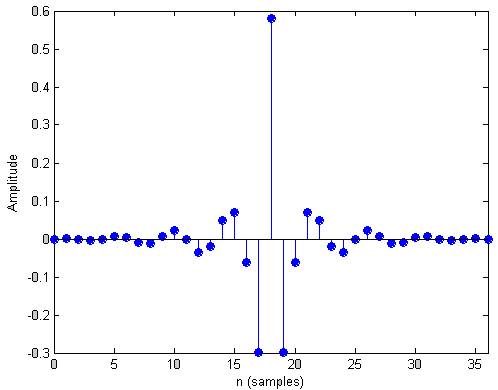
Рис.1 импульсная характеристика

Расчет частотных характеристик

[H,f]=freqz(a,1,[],1400);

plot(f,abs(H))

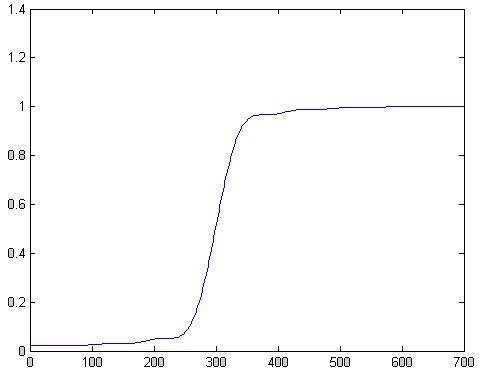
Рис.2 АЧХ

>> plot(f,unwrap(angle(H)))

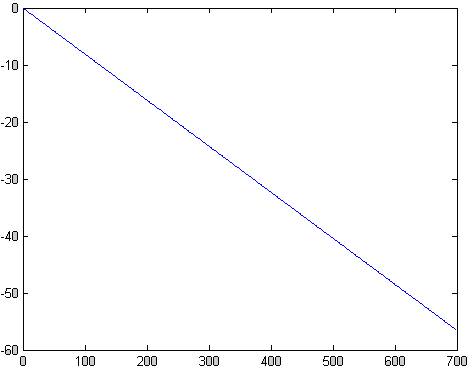
Рис.3 ФЧХ

2) смоделировать реакцию полученного цифрового фильтра на следующие воздействия

t=0:0.0005:0.0005*200;

s=sin(2*pi*500*t);

y=conv(s,a);

plot(t,y(1:201))

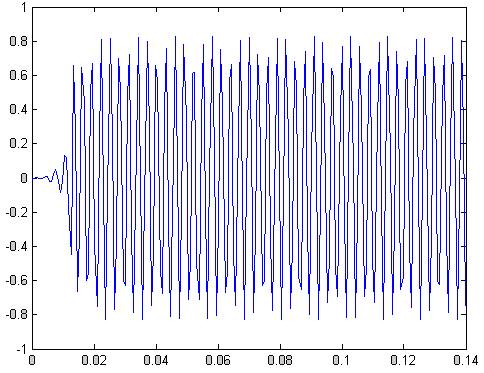
Рис.4 реакция фильтра на синусоидальный сигнал в зоне пропускания

s=sin(2*pi*650*t);

y=conv(s,a);

plot(t,y(1:201))

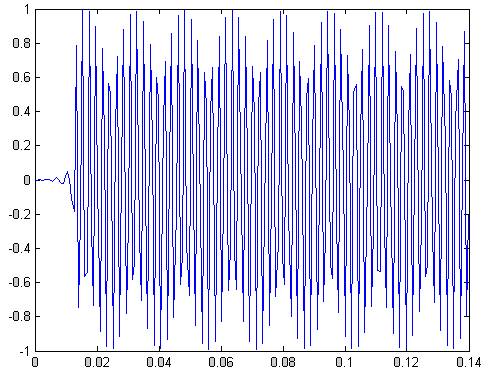
Рис.5 реакция фильтра на синусоидальный сигнал в зоне задерживания

s=sin(2*pi*500*t)+sin(2*pi*650*t);

y=conv(s,a);

plot(t,y(1:201))

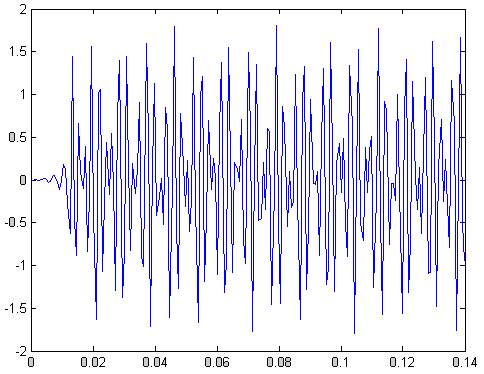
Рис.6 реакция на сумму синусоид

3) Исходя из заданных данных спроектировать нерекурсивный цифровой фильтр

a=firls(35,[0 0.37 0.59 1],[0 0 1 1]);

impz(a)

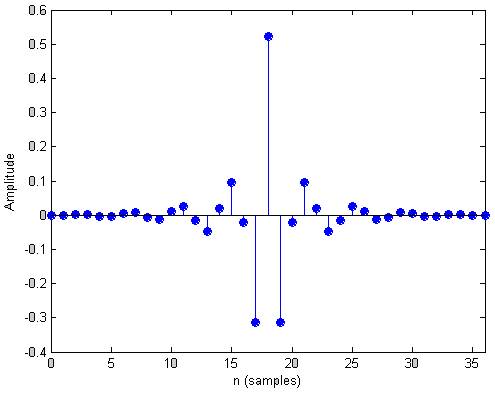
Рис.7 импульсная характеристика

Расчет частотных характеристик

[H,f]=freqz(a,1,[],1400);

plot(f,abs(H))

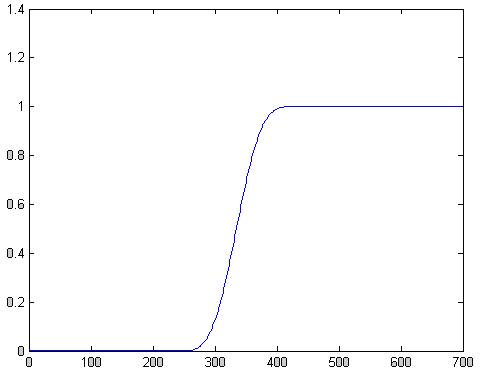
Рис.8 АЧХ

plot(f,unwrap(angle(H)))

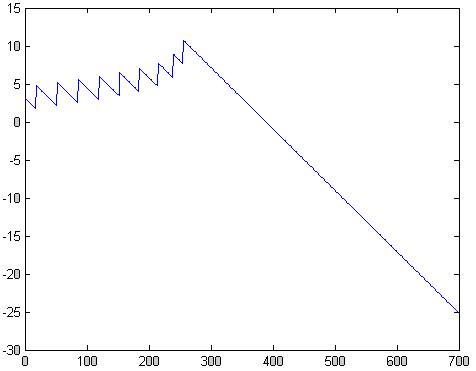
Рис.9 ФЧХ

s=sin(2*pi*500*t);

y=conv(s,a);

plot(t,y(1:201))

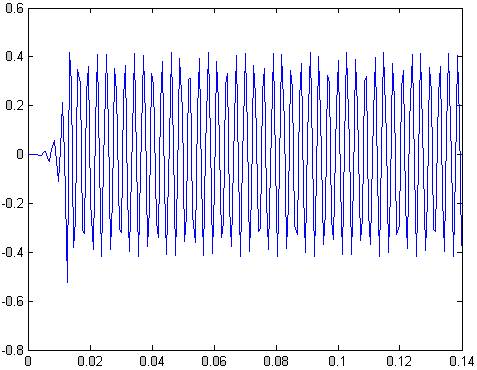
Рис.10 реакция фильтра на синусоидальный сигнал в зоне пропускания

s=sin(2*pi*650*t);

y=conv(s,a);

plot(t,y(1:201))

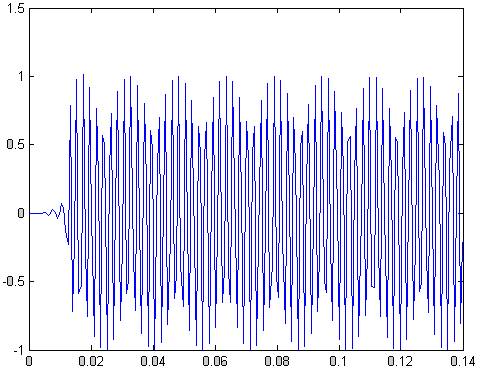
Рис.11 реакция фильтра на синусоидальный сигнал в зоне задерживания

s=sin(2*pi*500*t)+sin(2*pi*650*t);

y=conv(s,a);

plot(t,y(1:201))

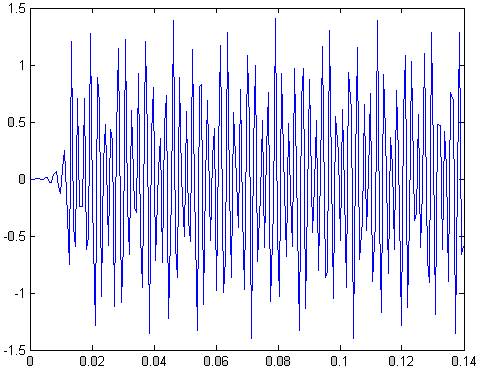
Рис.12 реакция на сумму синусоид

4. Исходя из заданных данных спроектировать нерекурсивный цифровой фильтр нижних и высоких частот с помощью метода весовых окон.

1) Фильтр низких частот

win=bartlett(36);

a=fir1(35,500/700,'low',win);

impz(a)

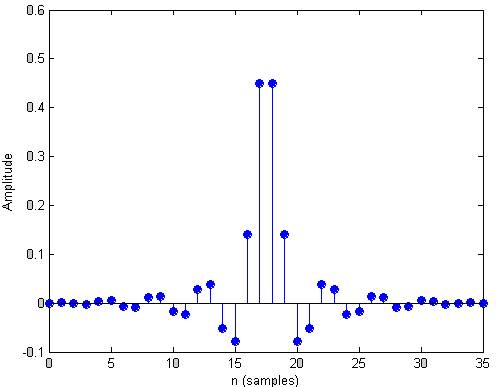
Рис.13 импульсная характеристика

Расчет частотных характеристик

[H,f]=freqz(a,1,[],1400);

plot(f,abs(H))

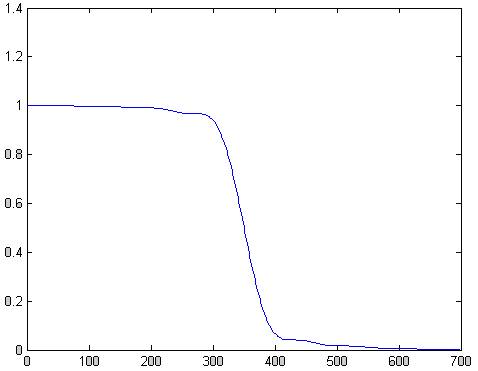
Рис.14 АЧХ

plot(f,unwrap(angle(H)))

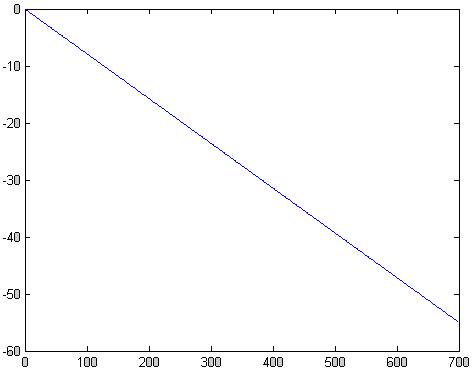
Рис.15 ФЧХ

2) смоделировать реакцию полученного цифрового фильтра на следующие воздействия

t=0:0.0005:0.0005*200;

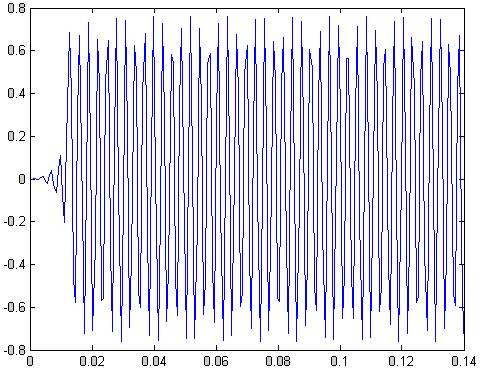
s=sin(2*pi*500*t);

y=conv(s,a);

plot(t,y(1:201))