Уравнения механики сплошной среды. Система уравнений механики сплошной среды

Лекция №1

Введение. Уравнения механики сплошной среды

Круг задач, охватываемых термином «газовая динамика» чрезвычайно широк. Это в первую очередь т. н. традиционные и наиболее развитые задачи внешней и внутренней аэродинамики (задачи обтекания тел и течения в каналах) до и - сверхзвуковых скоростей. А также относительно новые, связанные с гиперзвуковыми течениями, плазменными и химически реагирующими потоками, когда описание процессов невозможно в рамках совершенного газа с постоянным составом и теплоемкостью. Класс подобных задач и относится к физической газодинамике. Характерной особенностью их является высокий уровень температуры, когда в газе начинают происходить такие процессы, как возбуждение внутренних степеней свободы (вращательных, колебательных и т.д.), диссоциация молекул и ионизация атомов, излучение и поглощение лучистой энергии. Атомно-молекулярные процессы влияют на динамику течения и, наоборот, высокоскоростное движение среды изменяет ее теплофизические, оптические, электрические свойства и кинетику процессов. В настоящем курсе мы в меньшей степени будем касаться традиционных разделов газовой динамики и только в той части, где на простейших примерах можно получить понимание некоторых общих представлений. Основное внимание будет уделено изучению роли физических процессов как диссоциация, ионизация, излучение, явления переноса и т. п.

Система уравнений механики сплошной среды

Рассмотрим в неподвижной системе координат некий фиксированный элементарный объем газа V, для которого запишем основные законы сохранения массы, импульса и энергии

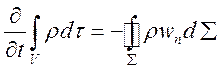                                                                                (1.1),

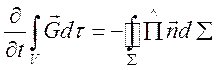                                                                                (1.2),

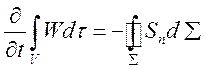                                                                                 (1.3).

Уравнение (1.1) выражает факт, что изменение массы в фиксированном объеме происходит за счет потока массы  через границу по нормали к площадке. Уравнение (1.2) выражает факт, что изменение полного количества движения в этом объеме  происходит за счет потока импульса:

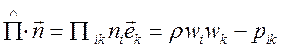                                                                        (1.4).

В (1.4) первый член в правой части связан с притоком импульса за счет движения жидкости через границу, а второй - тензор напряжений  связан с переносом импульса  за счет внутренних напряжений в среде. Если считать среду двух параметрической, т.е. все величины, характеризующие среду при термодинамическом равновесии (или в состоянии ЛТР) являются функциями двух переменных, то тензор напряжений будет иметь вид, где тензор вязких напряжений  есть

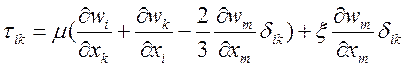                                                      (1.5).

Последнее равенство (1.3) выражает факт, что полное изменение энергии в рассматриваемом объеме происходит за счет потока энергии через границу.

Здесь 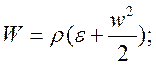 , где 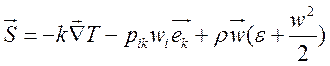, нормаль к поверхности. Первый член справа в выражении потока энергии есть кондукционный поток тепла.

Используя теорему Остроградского – Гаусса, система уравнений (1.1)-(1.3) может быть записана в дифференциальной форме:

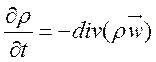                                                                                          (1.6).

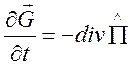                                                                                             (1.7).

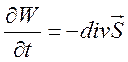                                                                                              (1.8).

Представление (1.6)-(1.8), так называемая дивергентная форма уравнений газовой динамики, часто используется при создании численных алгоритмов.

Система (1.6)-(1.8) является не замкнутой и для ее замыкания необходимо задать функции состояния системы: внутреннюю энергию и уравнение состояния.

В общем случае для определения функций состояния системы и получения замыкающих уравнений в рамках рассматриваемого феноменологического подхода необходимо воспользоваться законами термодинамики. Значение термодинамики состоит в том, что она дает возможность описать сложные системы со многими внутренними степенями свободы с помощью небольшого числа переменных. Наиболее простыми из них являются динамические переменные, такие как объем V, масса системы М и давление р, которое она оказывает на окружающую среду. Дополнительными переменными являются количества различных веществ n, составляющих исследуемую систему и её температура Т. Исследуемая система может состоять из нескольких гомогенных частей, называемых фазами. Химические вещества, составляющие фазу, называются её компонентами.

Если вещество рассматриваемой системы испытывает спонтанное изменение, то система не находится в состоянии равновесия. С другой стороны, если система, предоставленная самой себе, не изменяется, то она пребывает в равновесии с окружающей средой. Две системы, каждая из которой находится в равновесии с третьей системой, находятся в равновесии друг с другом. Постулируется, что системы находящиеся в равновесии друг с другом имеют одинаковую температуру. Это определяет понятие температуры. Произвольность в данном определении температуры устраняется только после выбора конкретной температурной шкалы. Наиболее употребительные линейные шкалы: термодинамическая (Кельвина), в которой задается Т = 0 К – наинизшая возможная температура, при которой прекращается всякое тепловое движение и Т = 273.16 К – температура плавления льда при р = 1 атм; практическая (Цельсия), в которой за 0 С принимается точка плавления льда, а за 100 С точка кипения воды при стандартном давлении 1 атм. Говорят, что система находится в нормальных условиях, когда её температура равна 273.16 К, а давление 1 атм.

Для системы находящейся в равновесии существует связь между термодинамическими переменными, описывающими её. Эта функциональная связь называется уравнением состояния:

                                                                                        (1.9).