Система не находящаяся в состоянии равновесия, вообще говоря будет испытывать изменения. Это может, например, иметь место при наличии потоков тепла, течения газа, при химических реакциях и т.д. В процессе изменения система может совершать работу А над окружающей средой. Работа представляет собой механическую величину, определяемую движением и силой. Когда изменения системы представляет собой бесконечно малое расширение то
![]() (1.10).
(1.10).
Первый закон термодинамики. С точки зрения статистической физики первый закон термодинамики представляет собой просто специальный случай сохранения энергии в механике: подведенное к системе тепло идет на изменение ее внутренней энергии и совершение работы
![]() (1.11).
(1.11).
Реальный процесс, который имеет место в природе, ведет систему к состоянию равновесия и не может быть обратимым. Строго обратимый процесс – понятие гипотетическое. Обратимые процессы фактически не имеют места, но реальные процессы могут приближаться к обратимым сколь угодно близко.
Второй закон термодинамики представляет собой утверждение того факта, что реальные процессы являются необратимыми. Второй закон термодинамики можно трактовать так:
Существует функция состояния системы S, называемая энтропией, изменение величины которой для термодинамического процесса удовлетворяет соотношению:
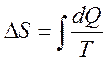 --
для обратимого процесса (1.12);
--
для обратимого процесса (1.12);
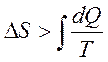 --
для реального процесса (1.13).
--
для реального процесса (1.13).
Первое равенство позволяет определить
энтропию системы с точностью до аддитивной постоянной ![]()
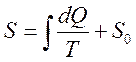 (1.14)
(1.14)
Второе соотношение указывает направление, в котором будет протекать термический процесс.
Третий закон термодинамики,
сформулированный Нернстом и Планком, позволяет определить значение константы![]() : энтропия всех веществ, при абсолютной
температуре Т = 0 равна нулю т.е.
: энтропия всех веществ, при абсолютной
температуре Т = 0 равна нулю т.е.![]() .
.
Для обратимого бесконечно малого изменения состояния системы, используя первый и второй законы термодинамики можно записать уравнение:
![]() (1.15).
(1.15).
Более подробно термодинамика газовых систем будет рассмотрена в следующих лекциях.
Представленные выше уравнения получены из феноменологических (макроскопических) рассмотрений основных физических законов сохранения. Однако входящие в них кинетические коэффициенты (коэффициенты вязкости, теплопроводности и т.п.) не могут быть найдены из феноменологической теории и для их определения требуются дополнительные соображения или эксперименты. В отличие от феноменологических теорий существует кинетический подход, базирующийся на использовании уравнения Больцмана, который позволяет получить не только макроскопические уравнения движения среды, но и выразить входящие в них коэффициенты через свойства газа. В то же время благодаря своей общности феноменологические теории позволяют построить уравнения (модели) для сложных сред, для которых кинетическая теория еще не развита.
Обобщение системы (1.6)-(1.8) в
случае учета дополнительных физических процессов осуществляется включением
соответствующих этим процессам членов в ![]() ,
, ![]() , W,
, W, ![]() и заданием дополнительных замыкающих уравнений.
Проиллюстрируем это на двух примерах.
и заданием дополнительных замыкающих уравнений.
Проиллюстрируем это на двух примерах.
1. Движение плазмы в электромагнитном поле.
Здесь необходимо учесть:
1) в ![]() плотность
электромагнитного количества движения
плотность
электромагнитного количества движения
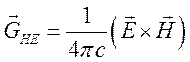 (1.16),
(1.16),
2) в ![]() плотность электромагнитной энергии
плотность электромагнитной энергии
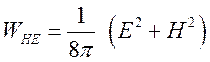 (1.77),
(1.77),
3) в ![]() плотность
потока электромагнитной энергии, (вектор Умова-Пойнтинга)
плотность
потока электромагнитной энергии, (вектор Умова-Пойнтинга)
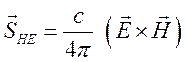 (1.88),
(1.88),
4) в ![]() тензор
плотности потока импульса электромагнитного поля
тензор
плотности потока импульса электромагнитного поля
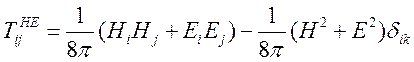 (1.19),
(1.19),
5) замыкающие уравнения, которые в магнитогидродинамическом приближении есть:
закон Ома для плотности тока
![]() =
= 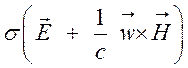 (1.20),
(1.20),
система уравнений Максвелла
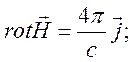
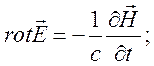
![]()
![]()
![]() (1.21).
(1.21).
2. Уравнения радиационной газодинамики
В общем случае перенос излучения и лучистый теплообмен влияют на состояние вещества, на его движение и распределение термодинамических параметров. Это влияние связано с тем, что испуская и поглощая излучение, вещество теряет или приобретает энергию, импульс и массу. Здесь необходимо учесть:
1) в левой части уравнения неразрывности (1.6)—релятивистскую массу поля излучения
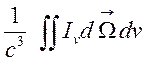 (1.22),
(1.22),
2) в правой части (1.6)—поток этой массы
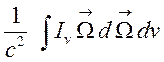 (1.23),
(1.23),
3)
в ![]() импульс фотонов
импульс фотонов
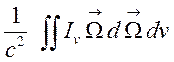 (1.24),
(1.24),
4) в ![]() --
тензор радиационных напряжений
--
тензор радиационных напряжений
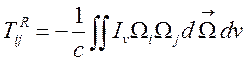 (1.25),
(1.25),
5) в W– плотность лучистой энергии
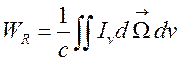 (1.26),
(1.26),
6) в ![]() радиационный
поток энергии
радиационный
поток энергии
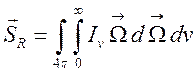 (1.27),
(1.27),
7) в качестве замыкающего уравнения – уравнение переноса излучения
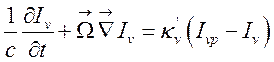 (1.28).
(1.28).
Здесь ![]() интенсивность
излучения (спектральный поток энергии излучения в элементе телесного угла
интенсивность
излучения (спектральный поток энергии излучения в элементе телесного угла ![]() в направлении
в направлении ![]() ),
), ![]() спектральный коэффициент поглощения,
исправленный на вынужденное испускание,
спектральный коэффициент поглощения,
исправленный на вынужденное испускание, 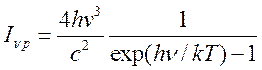 - спектральная интенсивность
равновесного излучения.
- спектральная интенсивность
равновесного излучения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.