Термодинамика различных систем. Равновесное тепловое излучение. Поверхностное натяжение

7. Термодинамика различных систем

Равновесное тепловое излучение. В качестве примера исследования произвольных термодинамических систем рассмотрим сначала  так называемый фотонный газ, находящийся в тепловом равновесии. С феноменологической точки зрения это излучение «чёрного тела». Этот образ позволяет отличить равновесное излучение от неравновесного, каким является излучение любого источника (лампа, лазер, излучение тела, выведенного из равновесия со средой). Аналогом такой неравновесной системы является молекулярный пучок. Но если излучение замкнуто в «чёрном», то есть в непроницаемом для него ящике, то это термодинамическая система в равновесии с «ящиком», т. е. с окружающей средой. Стенки «ящика» достаточно толстые (в идеале бесконечно толстые), а сам он находится при температуре Т = const. Находящееся в его полости излучение и называют тепловым или «черным».

          Важнейшей особенностью системы является то, что от занимаемого объема V зависит количество излучения, но не его свойства, которые определяются только температурой. В этом отношении излучение в равновесии со стенками «чёрного ящика» подобно пару над поверхностью жидкости. Увеличение полости, занятой излучением (паром), приводит к увеличению числа фотонов (молекул) в ней, оставляя неизменным давление на стенки, а также плотности всех экстенсивных величин (числа частиц, внутренней энергии, энтропии и свободной энергии):

              N = nV, U = uV, S = sV, F = fV,                           (190)

где соответствующие плотностиu(T), s(T), f(T) – функции только температуры. Что касается давления света, то оно, согласно выражениям (140), есть 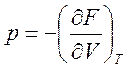  и также является только функцией температуры, причем методами термодинамики в совершенно общем случае устанавливается связь его с плотностью энергии:

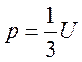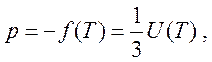                           ,                              (191)

т. е. электродинамической информации первой формулы вполне достаточно, чтобы, считая теперь излучение равновесным, определить термодинамическими методами  зависимость u(T) плотности внутренней энергии излучения от его от температуры.

          Заметим, что для построения полной термодинамики системы нам, как указывалось, необходимо знание термического уравнения состояния и теплоемкости , удовлетворяющей соотношению (111) (условию полного дифференциала для внутренней энергии). В рассматриваемом случае «заданным» согласно уравнениям (190) и (191) является общий вид термического и калорического уравнений состояния. Этого оказывается достаточно для построения термодинамики. Действительно, используя «термодинамическое  уравнение состояния» (109) (или (110)) получим:

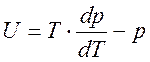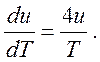                            или                              (192)

Интегрируя второе уравнение (192) получим

                                             ,                                                (193)

где  есть мировая постоянная, независимая от природы «чёрного ящика». Если бы это было не так, то при одной и той же температуре в разных ящиках устанавливалась бы разная плотность излуче­ния, и при соединении их световодом поток излучения устремлялся бы из одного в другой, стремясь уравнять плотности излучения. Это привело бы к охлаждению одного ящика и нагреву другого, вопреки принципу Клаузиуса. Постоянная , пропорциональная постоянной Стефана–Больцмана, может быть установлена только микроскопическим рассмотрением. Строго говоря постоянная Стефана–Больцмана есть пропорциональная величине  величина, определяющая плотность потока лучистой энергии

                                                    (194)

Учитывая уравнения (191), имеем

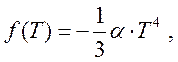                                                                            (195)

откуда для плотности энтропии (см. выражения (140), (190)) и соответственно теплоемкости имеем выражения

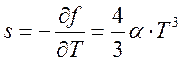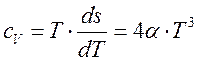                   ,                       (196)

в полном соответствии с принципом Нернста.

Заметим, что из выражений (193) и (190) для внутренней энергии U можно получить выражение для свободной энергии  F, если уравнение состояния неизвестно. Используя уравнение Гиббса–Гельмгольца (144) и  выражение для внутренней энергии (калорическое уравнение состояния)  получим

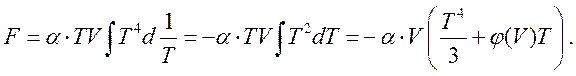          (197)

Используя теперь принцип Нернста,

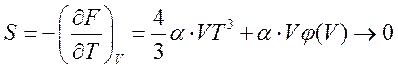 при                    (198)

найдем . При этом из полученного выражения автоматически следует линейная зависимость свободной энергии F от   от объема V  (см. выражение (190)) и уравнение состояния 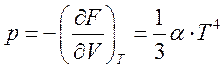. Нахождение уравнения состояния с использованием формулы (197) определяет давление р с точностью до линейной функции температуры.