Упражнения по курсу «Обобщенные решения уравнений математической физики (Доказать, что если определитель есть линейная функция, то прямая является линией ранга 1)

Матвеева Анна,

Гр.4132

Упражнения по курсу «Обобщенные решения уравнений математической физики»

Упражнение 1: Доказать

Решение:

Т.е. надо доказать: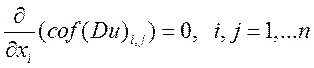

Из курса Высшей Алгебры известно: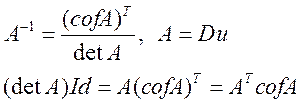

                                                                                                       (1)

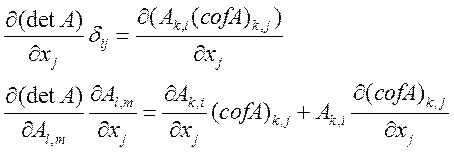
Используем тот факт, что:  зависит только от ,

Тогда из (1):  =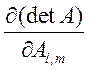

Вводим переобозначение индексов:

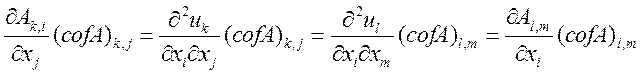
Получаем: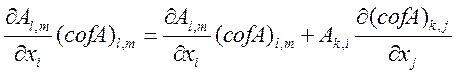

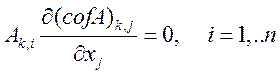
Или

Если Du обратима, тогда , что и требовалось доказать. Если нет, то:

Пусть . Тогда обратима для любых сколь угодно малых

При  упражнение доказано.

Упражнение 2: Доказать

Решение:

 

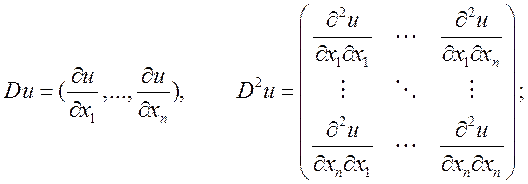
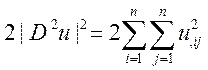
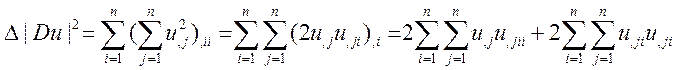
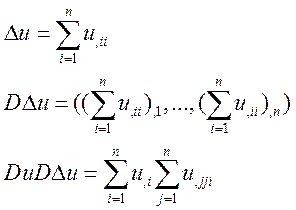
Итак:

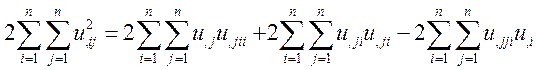
Используя, , получаем тождество.

Что и требовалось доказать.

Упражнение 3.

Не существует точных нетривиальных решений

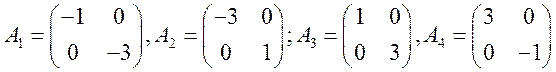
Доказательство:

Докажем, что если

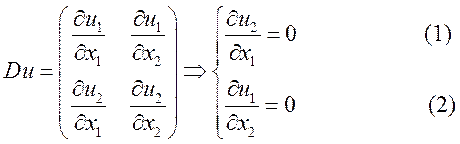
Из (1) следует, что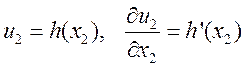

Т.к. элемент (2,2) для различен, по  можно определить матрицу

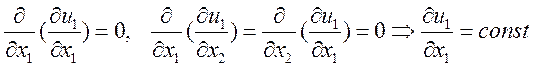
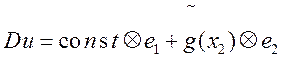                                                                                               (3)

Аналогично, из (2) следует, что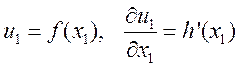

Т.к. элемент (1,2) для различен, по  можно определить матрицу

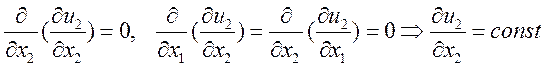
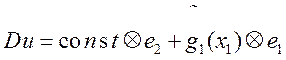                                                                                               (4)

Из (3), (4) следует, что Du=const,

Упражнение доказано.

Упражнение5:

            Дано:

           

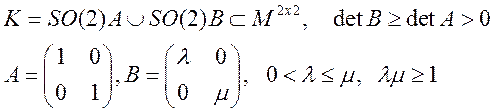
            Доказать:

1)  Если , то К не содержит связей ранга 1

2)  Если , то каждой матрице из К можно сопоставить ровно одну матрицу из К, вязанную рангом 1.

3)  Если , то каждой матрице из К можно сопоставить ровно две матрицы из К, вязанных рангом 1.

Решение:

Рассмотрим . Возможно, несколько случаев:

a) , тогда

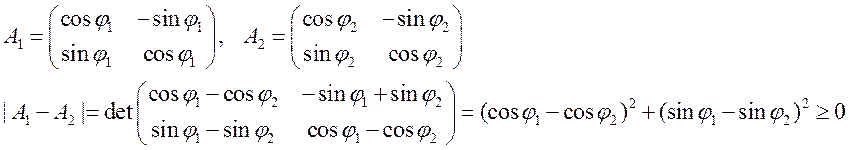
Равенство достигается, только тогда, когда . Следовательно, в нет связей ранга 1.

b)

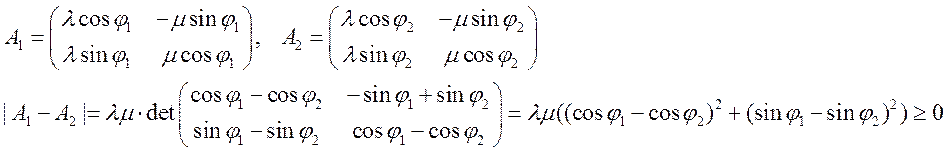Аналогично 1), получаем, нет связей ранга 1.

c)

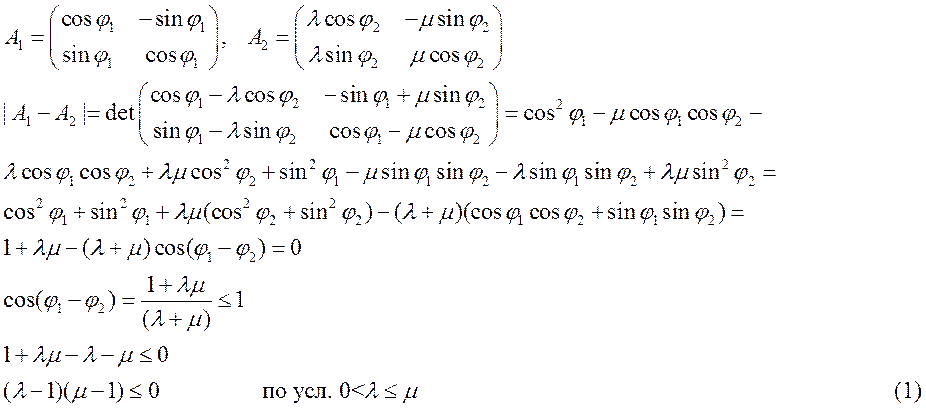
1)  , тогда неравенство (1) неверно и в К нет связей ранга 1.

2) , то в (1) достигается равенство, тогда

         то каждой матрице из К можно сопоставить ровно одну матрицу из К (с точностью до), вязанную рангом 1.

3), тогда

        

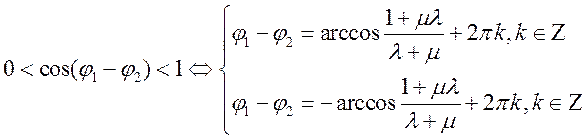
         Т.е. каждому  можно сопоставить 2 значения  с точностью до , и наоборот,  каждому  — 2 значения

         Таким образом,  каждой матрице из К можно сопоставить ровно две матрицы из К, вязанных рангом 1.

Упражнение доказано.

Упражнение 6: 

            В пространстве матриц 2x2 есть прямая, заданная параметрическим способом.

            Доказать, что если определитель есть линейная функция, то прямая является     линией ранга1.

Решение:

            Если Х1 и Х2 связаны рангом  1, то прямая Х, соединяющая Х1 и Х2, есть линия ранга 1.

Рассмотрим   , где           

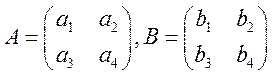
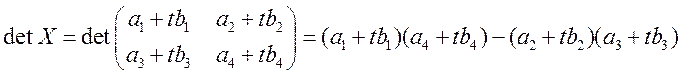                             (2)

Т.к. по условию, определитель — линейная функция, то коэффициент при  в (2) равен 0.

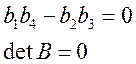                                                                                                                        (3)

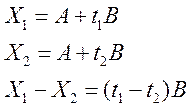
Из (3) следует, что

Что и означает, что прямая в пространстве матриц 2х2  является линией ранга 1.

Упражнение доказано