Термодинамика различных систем. Равновесное тепловое излучение. Поверхностное натяжение, страница 3

Здесь объем V считается постоянным, и термодинамическими параметрами являются Е, D, T, причем выражение (212), связывающее величины Е, D, T есть термическое уравнение состояния. Из этого следует, что, переходя от формул термодинамики газов к формулам термодинамики диэлектриков, надо сделать замену:

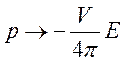                                 ,                            (214)

Мы, как указывалось, пренебрегаем электрострикцией и пьезоэлектрическим эффектом, полагая в выражениях (212) и (213) V= const.. Дифференциал внутренней энергии есть

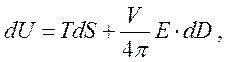                                                          (215)

аналог теплоемкости  есть теплоемкость , а аналог теплоемкости  есть теплоемкость ; основные термодинамические тождества для исключения энтропии имеют вид

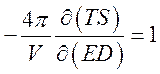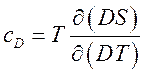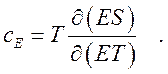,      ,         (216)

С помощью соотношения (212) 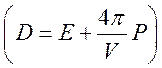 выражение (213) для работы можно представить в виде

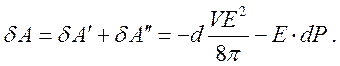                                        (217)

Вводя новую термодинамическую функцию

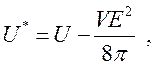                                                                      (218)

получим вместо дифференциала (215) дифференциал

                                                                  (219)

функции , для которой собственными переменными являются энтропия S и поляризация P. Следует иметь ввиду, что величина E – электрическое поле, искаженное присутствием диэлектрика, и  величина  не имеет смысла внутренней энергии за вычетом энергии электрического поля в вакууме.  Стандартная замена перехода от газовой термодинамики к термодинамике диэлектриков в указанных переменных есть

                                     , ,                             (220)

аналог есть , а аналог  есть , и

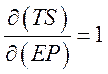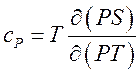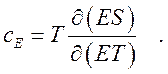            ,    ,         (221)

          Совершенно аналогично рассматривается термодинамика пара- и диамагнетиков, помещенных во внешнее магнитное поле Н. Вектор намагничивания есть

                                                                         (222)

где  – магнитная восприимчивость, описываемая второй  формулой (211) для парамагнетиков (намагниченность обусловлена магнитными моментами молекул) и первой формулой для  диамагнетиков (<0), обладающих наведенным магнитным моментом вследствие Ларморовской прецессии электронов в магнитном поле. Введем вектор магнитной  индукции

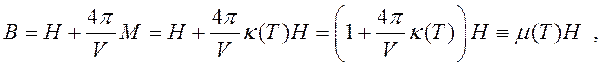
где

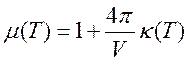                                                                (223)

– магнитная проницаемость вещества. Таким образом, работа, совершаемая магнитным полем, есть

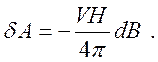                                                                      (224)

Стандартная замена для перехода от формул термодинамики газов к термодинамике магнетиков есть

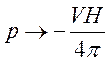                              ,                                 (225)

Дифференциал внутренней энергии есть .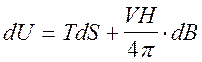

Аналог теплоемкости  есть теплоемкость , а аналог теплоемкости есть теплоемкость  и

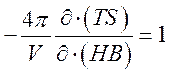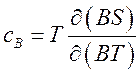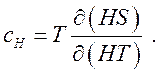          ,  ,    (226)

Аналогично случаю диэлектриков, в рассматриваемом случае  можно перейти к переменным Н и М, введя

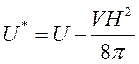
                                       (227)

Таким образом, формальное отличие термодинамики магнетиков и диэлектриков –  в замене буквенных обозначений.

          В качестве примера рассчитаем количество тепла, выделяющееся (поглощающееся) в диэлектрике при изотермическом включении поля с напряженностью Е. Используем при этом термодинамический потенциал Гиббса с собственными переменными Т и Е:

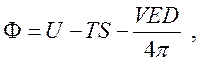                                                               (228)

или

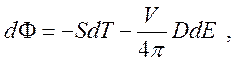                                                         (229)

причем   . Интегрируя выражение (229) имеем

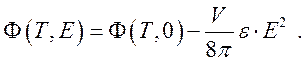                                              (230)

Так как 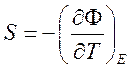, то из выражения (230) получим

                         

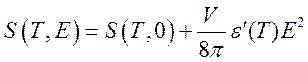
или при постоянной температуре (Т = const)  имеем количество теплоты

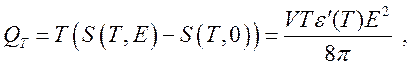                            (231)

где  есть производная по температуре от величины .  Для неполярных диэлектриков – и , для полярных диэлектриков 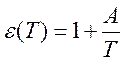  (А>0) и

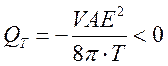                                             ,                                        (232)

т. е. тепло выделяется. Физически это очевидно. Действительно, при включении электрического поля над диэлектриком совершается работа. Вместе с тем потенциальная энергия диполей уменьшается вследствие ориентации диполей по полю. Поэтому кинетическая энергия, а вместе с ней и температура должны были бы возрастать. Но так как процесс происходит при постоянной температуре (Т = const), то тепло должно отводиться в термостат.

          В  принципе для построения полной термодинамики, наряду с уравнением состояния, необходимо знание какой-либо из теплоемкостей.