Термодинамика различных систем. Равновесное тепловое излучение. Поверхностное натяжение, страница 2

Поверхностное натяжение. При наличии границы раздела жидкой и газообразной фазы эта граница не является плоской, а есть переходная область конечной толщины со своими свойствами, отличными от свойств гомогенных фаз. Поэтому свободная энергия реальной системы отличается от свободной энергии идеальной системы,  разделенной абсолютно резкой границей. Поскольку избыток свободной энергии возникает при учете поверхности раздела, он прямо пропорционален её площади S.  Эту площадь можно изменять в определенных пределах, изменяя форму жидкости, но это требует усилий, противостоящих силам поверхностного натяжения. Если, например, жидкость находится в рамке с подвижной планкой  (рис.  19),

        

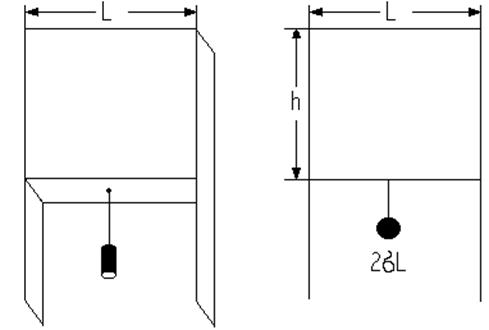
                        Рис. 19. Силы поверхностного натяжения

то ее обе поверхности (фронтальная и тыловая) действуют на планку длины  с силой . Чтобы обратимо растянуть жидкость, требуется приложить силу  , которая при смещении на dh произведет работу

                               ,                         (199)

Видно, что формальное отождествление с газовой термодинамикой можно осуществить, положив ,  . Используя выражение (142) имеем:

                                при  Т=const                                 (200)

или

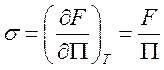                      ,                                      (201)

Этот результат является следствием того факта, что поверхностное натяжение зависит только от температуры Т и ни от чего больше:

                                           ,                                             (202)

т. е. поверхностная фаза является еще одной системой, подобной излучению и пару: ее можно увеличить количественно, развивая поверхность, но все ее остальные свойства определяются исключительно температурой. Сама величина поверхностного натяжения  является удельным (на единицу площади) избытком свободной энергии поверхности, а уравнение (202) является аналогом уравнения состояния для газов, т. е. уравнением состояния данной системы. Также существуют удельные избытки внутренней энергии и энтропии:

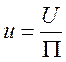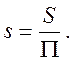                                        ,                                          (203)

В соответствии с уравнением Гиббса–Гельмгольца (144) и (140) имеем

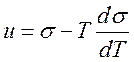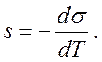                                ,                                  (204)

Это означает, что знание  зависимости  позволяет построить термодинамику поверхностного натяжения, например, найти «скрытую» теплоту образования единицы площади жидкой пленки в изотермическом процессе:

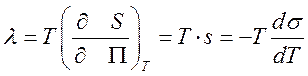
                            (205)

          Если принимать во внимание поверхностные эффекты, то изменение свободной энергии F в системе жидкость–пар при постоянной температуре (Т = const)есть

                                                    (206)

где индекс 1 относится к жидкой, а 2 – к газовой фазе. Если имеем каплю жидкости сферической формы, то

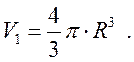                              ,                            (207)

Используя эти выражения  в выражении (206) получим

                                          (208)

где  – перепад давлений между жидкостью и паром, который однозначно определяется равенством нулю коэффициента  при величине dR:

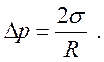                                                                                   (209)

Это известная формула Лапласа, утверждающая, что давление внутри капли выше, чем под плоской поверхностью жидкости.

Диэлектрики и магнетики. Рассмотрим термодинамические свойства поляризующихся сред (диэлектриков), помещенных в электрическое поле Е. Как известно из электродинамики, такое поле взаимодействует с дипольными моментами молекул (полярный диэлектрик) или с наведенными дипольными моментами (неполярный диэлектрик), вызывая их ориентацию вдоль направления поля (поляризация). Вектор поляризации (электрический дипольный момент) есть

                                          ,                                       (210)

т. е. он направлен по полю и, в отсутствие насыщения, пропорционален его величине. Электрическая восприимчивость , зависящая только от температуры, есть

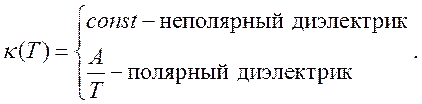                              (211)

Вектор индукции D, учитывающий искажение поля, наличием диэлектрика, есть

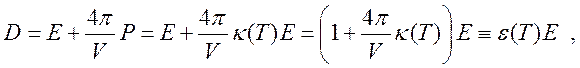        (212)

где 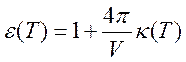 – диэлектрическая проницаемость вещества. Работа, совершаемая источником электрического поля есть

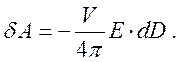                                                                        (213)